2017年 日本数学オリンピック本選 第3問 解答例
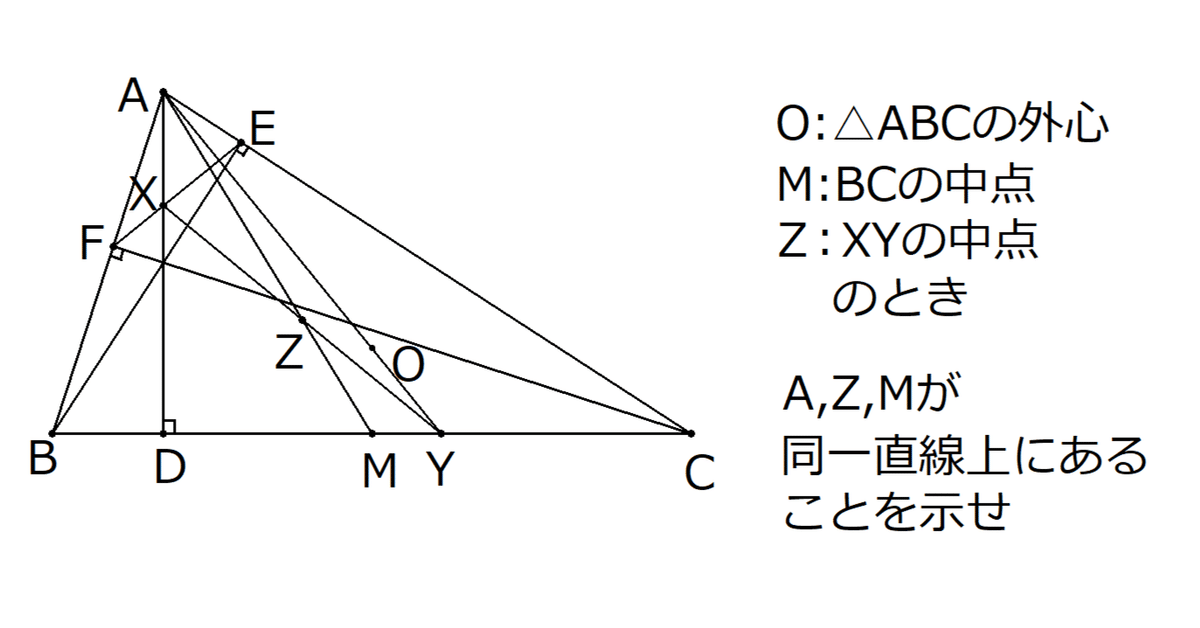
鋭角三角形$${ABC}$$があり、その外心を$${O}$$とする。3点$${A, B, C}$$から対辺におろした垂線の足をそれぞれ$${D, E, F}$$とし、さらに辺$${BC}$$の中点を$${M}$$とする。直線$${AD}$$と直線$${EF}$$の交点を$${X}$$, 直線$${AO}$$と直線$${BC}$$の交点を$${Y}$$とし、線分$${XY}$$の中点を$${Z}$$とする。このとき3点$${A, Z, M}$$が同一直線上にあることを示せ。
考え方:
3点が同一直線上にあることを示すのは簡単ではないです。
ただ、今回の問題は、$${AM}$$と$${XY}$$の交点が$${XY}$$の中点になることを示すのと同値です。
これならば、メネラウスの定理を使えば何とかなりそうです。
下記の解答例ではあえて三角比・三角関数を使わないでゴリ押してみました。
見た目ほど計算は大変ではありません、この問題に挑戦する人ならこれくらいはこなすだろうなと思い載せてみました。
出てくる数式にある程度対称性があるので、悪くない解き方だと思います。
図中に、メネラウスの定理が使えるパーツがいくつもあるので、
そこを組み合わせて、最終的に$${XZ:YZ}$$を求められる形に変形していきます。
各辺の長さを$${a, b, c}$$でおいてやれば、
主要な部分の長さは(多少面倒ですが)さほど難なく$${a, b, c}$$を使って表せますので、
最後までゴリ押せます。
が、三角比と正弦定理を駆使すればこれよりは少ない計算量で示すことができました。
あえて解答例としては載せませんが、それもぜひ試してみてください。
解答例:

$${XY}$$と$${AM}$$の交点が$${XY}$$の中点であることを示せばよい。
そこで、$${XY}$$と$${AM}$$の交点を$${Z'}$$とおいたときに$${XZ' = YZ'}$$を示せばよいが、
メネラウスの定理より、
$$
\frac{AD}{XA}\frac{MY}{DM}\frac{XZ'}{YZ'} = 1
$$
であるから、
$$
\frac{AD}{XA}\frac{MY}{DM} = 1
$$
を示せばよい。
$${BC = a, CA = b, AB = c}$$とおく。
$${BD^2 + AD^2 = c^2, DC^2 + AD^2 = b^2, BD+DC = a}$$
を解いて、
$${BD = \frac{a^2-b^2+c^2}{2a}, DC = \frac{a^2 +b^2 - c^2}{2a}, AD =\frac{t}{2a}}$$
を得る。ただし、$${t = \sqrt{2a^2b^2 +2b^2c^2 +2c^2a^2 -a^4 -b^4 -c^4} }$$である。
同様の計算により、
$${CE = \frac{a^2+b^2-c^2}{2b}, EA = \frac{-a^2 +b^2 + c^2}{2b}, BE =\frac{t}{2b}}$$
$${AF = \frac{-a^2+b^2+c^2}{2c}, FB = \frac{a^2 -b^2 + c^2}{2c}, CF =\frac{t}{2c}}$$
を得る。
$${\angle BOM =\angle BOC / 2 = \angle BAC}$$であり、
$${\angle BMO = 90^{\circ} = \angle BEA}$$であるから、
三角形$${BOM}$$と三角形$${BAE}$$は相似である。
よって、
$${OM = BM \cdot \frac{AE}{BE} = \frac{a}{2}\frac{-a^2+b^2+c^2}{2b} \frac{2b}{t} = \frac{-a^2+b^2+c^2}{2t}a}$$
となる。これより、
$$
\begin{align*}
\frac{MY}{DM} &= \frac{OM}{AD-OM} \\
&= \frac{-a^2+b^2+c^2}{2t}a \frac{1}{ \frac{t}{2a} -\frac{-a^2+b^2+c^2}{2t}a} \\
&= \frac{-a^2+b^2+c^2}{2t} \frac{2a^2t}{t^2-(-a^2 + b^2+c^2)a^2}\\
&= \frac{a^2(-a^2+b^2+c^2)}{a^2b^2+2b^2c^2+c^2a^2-b^4-c^4}
\end{align*}
$$
となる。
さて、三角形$${ABC}$$の垂心を$${H}$$とすると、
メネラウスの定理と、三角形$${BHF}$$と三角形$${BAE}$$が相似なことより
$$
\begin{align*}
\frac{XH}{AX} &= \frac{HF}{FC}\frac{CE}{EA} \\
&= \frac{BF}{BE}\frac{CE}{FC} \\
&=\frac{a^2 -b^2 + c^2}{2c}\frac{2b}{t}\frac{a^2+b^2-c^2}{2b}\frac{2c}{t} \\
&= \frac{(a^2 - b^2 +c^2)(a^2+b^2-c^2)}{t^2}
\end{align*}
$$
より
$$
\begin{align*}
\frac{AH}{AX} &= \frac{XH + AX}{AX} \\
&= \frac{(a^2 - b^2 +c^2)(a^2+b^2-c^2)}{t^2} + 1\\
&= \frac{-2b^4-2c^4 + 2a^2b^2 +4b^2c^2+2c^2a^2}{t^2}
\end{align*}
$$
同じくメネラウスの定理より、
$$
\begin{align*}
\frac{HD}{AH} &= \frac{DB}{BC} \frac{CE}{EA} \\
&= \frac{a^2-b^2+c^2}{2a}\frac{1}{a}\frac{a^2+b^2-c^2}{b^2 -a^2+c^2} \\
&= \frac{(a^2-b^2+c^2)(a^2+b^2-c^2)}{2a^2(b^2-a^2+c^2)}
\end{align*}
$$
より
$$
\begin{align*}
\frac{AD}{AH} &= \frac{AH + HD}{AH} \\
&= \frac{(a^2-b^2+c^2)(a^2+b^2-c^2) + 2a^2(b^2-a^2+c^2)}{2a^2(b^2-a^2+c^2)}\\
&= \frac{t^2}{2a^2(b^2-a^2+c^2)}
\end{align*}
$$
となるので、
$$
\begin{align*}
\frac{AD}{AX} &= \frac{AH}{AX}\frac{AD}{AH} \\
&= \frac{-2b^4-2c^4 + 2a^2b^2 +4b^2c^2+2c^2a^2}{t^2}\frac{t^2}{2a^2(b^2-a^2+c^2)} \\
&= \frac{-b^4-c^4+a^2b^2+2b^2c^2+c^2a^2}{a^2(b^2-a^2+c^2)}
\end{align*}
$$
以上を合わせ
$$
\begin{align*}
\frac{AD}{XA}\frac{MY}{DM}& = \frac{-b^4-c^4+a^2b^2+2b^2c^2+c^2a^2}{a^2(b^2-a^2+c^2)} \frac{a^2(-a^2+b^2+c^2)}{a^2b^2+2b^2c^2+c^2a^2-b^4-c^4}\\
&=1
\end{align*}
$$
となり、題意は示された。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
