2012年 日本数学オリンピック本選 第1問 解答例
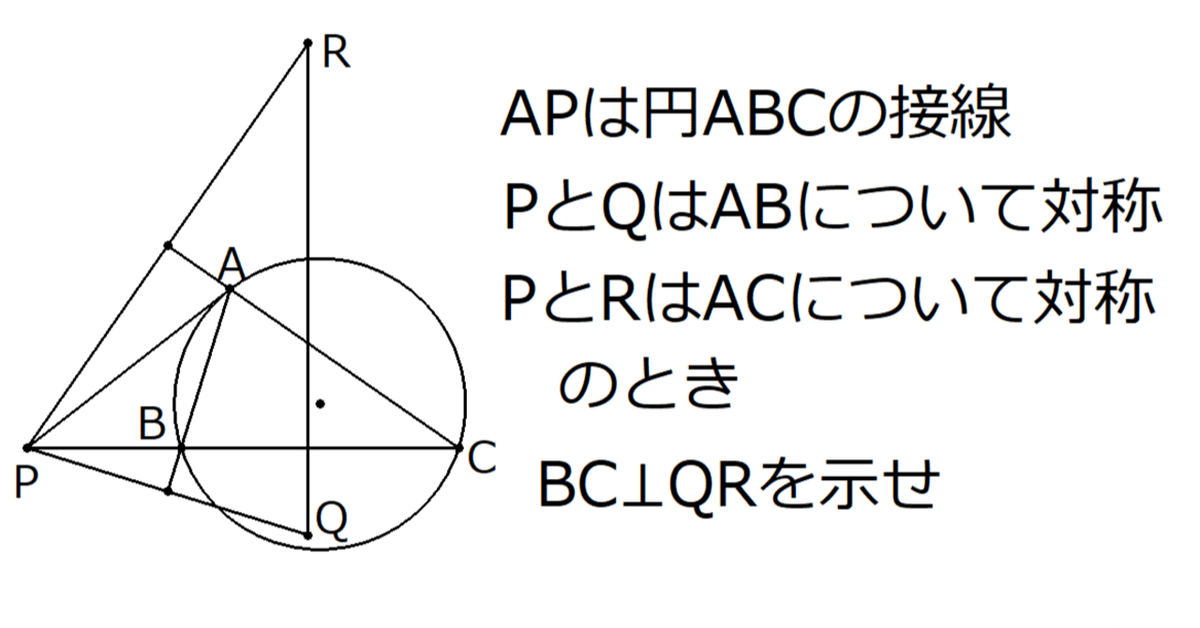
三角形$${ABC}$$があり、その外接円の$${A}$$での接線と直線$${BC}$$が点$${P}$$で交わっている。直線$${AB, AC}$$について点$${P}$$と対称な点をそれぞれ点$${Q, R}$$とする。この時、直線$${BC}$$と直線$${QR}$$は垂直に交わることを示せ。
考え方:
直線について対称な点という条件から円に内接する四角形の存在に気づければ、
角度を追うだけであっさり解決します。
基本をおさえていればサービス問題と言えます。
解答例:

条件より$${AB \neq AC}$$である。
$${AB<AC}$$とする。
直線$${AB}$$と直線$${PQ}$$の交点を$${S}$$、
直線$${AC}$$と直線$${PR}$$の交点を$${T}$$、
直線$${ST}$$と直線$${BC}$$の交点を$${D}$$とする。
条件より$${PQ}$$と$${ST}$$は平行であるから、
$${ST}$$と$${BC}$$が垂直であることを示す。
$${\angle ABC \neq 90^{\circ}}$$のとき、
$${\angle ASP = \angle ATP = 90^{\circ}}$$なので、
四角形$${ASPT}$$(または四角形$${ATSP}$$)は円に内接する。
よって$${\angle PAS = \angle PTS}$$である。
また、接弦定理より$${\angle PAS = \angle TCP}$$である。
よって、$${\angle PTS = \angle TCP}$$であるため、
$${\angle TDP = \angle CTP = 90^{\circ}}$$である。
よって$${ST}$$と$${BC}$$は垂直である。
$${\angle ABC = 90^{\circ}}$$のとき、
$${T}$$と$${A}$$は一致し、$${S}$$と$${B}$$は一致するため
$${ST}$$と$${BC}$$は垂直になる。
$${AB>AC}$$のときは、$${B}$$と$${C}$$を入れ替えれば同じ議論により結論を得る。
追記:
三角形$${ABC}$$が$${\angle B > 90^{\circ}}$$の鈍角三角形のとき、
$${T}$$と$${S}$$は$${AP}$$から見て同じ側に位置する形状となりますが、
上記議論はそのまま成立します。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
