2023年 日本数学オリンピック本選 第2問 解答例
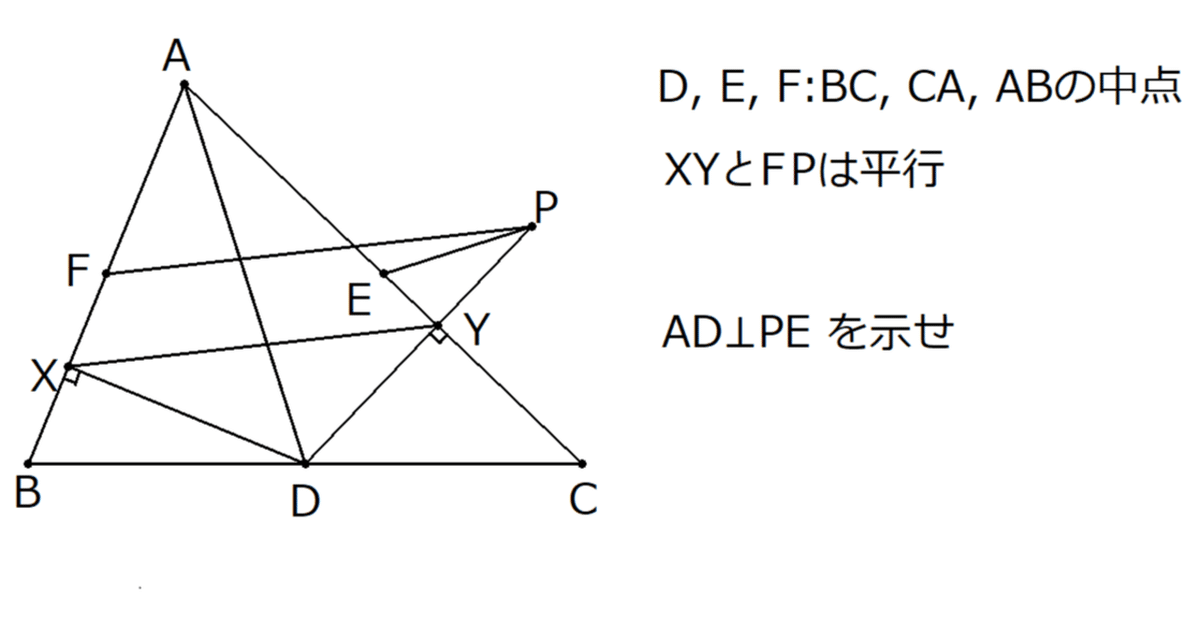
鋭角三角形$${ABC}$$があり、辺$${BC, CA, AB}$$の中点をそれぞれ$${D, E, F}$$とし、$${D}$$から辺$${AB, AC}$$におろした垂線の足をそれぞれ$${X, Y}$$とする。$${F}$$を通り直線$${XY}$$に平行な直線と直線$${DY}$$が$${E}$$と異なる点$${P}$$で交わっている。このとき、直線$${AD}$$と直線$${EP}$$は垂直に交わることを示せ。
考え方:
この問題も角度を調べていけば難なく求まります。
これまでの練習の成果を試すにはちょうどいい問題です。
解答例:

$${\angle AXD = \angle AYD = 90^{\circ}}$$より,
$${A, X, D, Y}$$は同一円周上にある。
よって、$${\angle XAD = \angle XYD = \angle FPD}$$となり、
$${A, F, D, P}$$は同一円周上にある。
$${AC}$$と$${FD}$$は平行であるから、
$${\angle PDF = \angle DYC = 90^{\circ}}$$より、
$${\angle FAP = 180^{\circ} - \angle PDF = 90^{\circ}}$$
となり、$${DE}$$と$${AB}$$は平行なので$${DE}$$と$${AP}$$は垂直に交わる。
よって、$${E}$$は三角形$${ADP}$$の垂心であり、
$${AD}$$と$${PE}$$は垂直に交わる。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
