2010年 日本数学オリンピック本選 第1問 解答例
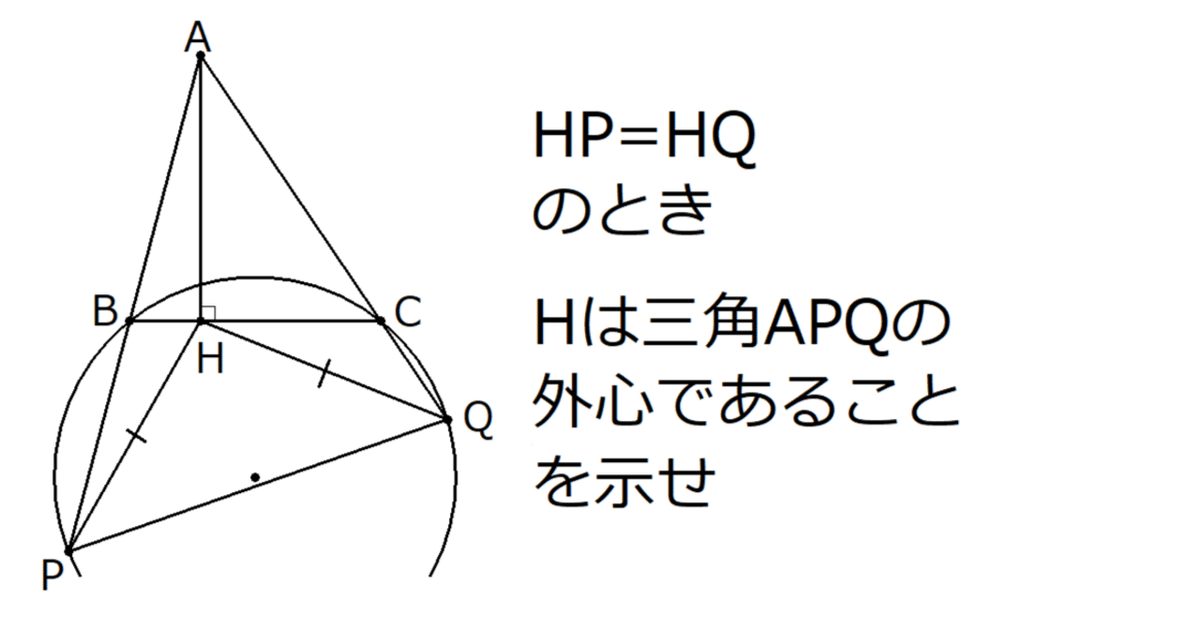
$${AB \neq AC}$$なる鋭角三角形$${ABC}$$があり、$${A}$$から$${BC}$$におろした垂線の足を$${H}$$とおく。点$${P, Q}$$を、$${3}$$点$${A, B, P}$$と$${3}$$点$${A, C, Q}$$がともにこの順に一直線上に並ぶようにとると、$${4}$$点$${B, C, P, Q}$$は同一円周上にあり、$${HP=HQ}$$が成り立った。このとき$${H}$$は三角形$${APQ}$$の外心であることを示せ。
ただし、$${XY}$$で線分$${XY}$$の長さを表すものとする。
考え方:
二等辺三角形と内接四角形の存在から角度の関係を調べ、
正弦定理と三角関数の公式を駆使すれば難なく結論が出ます(別解)。
ただ、本選の第1問で三角関数を駆使しないといけない問題は他になく、
適した解き方と言えるかは少し迷いました。
三角関数をあえて使わないで解こうとすると、意外に厄介です。
とはいえ、条件と示すものを逆にした問題、つまり、
$${H}$$が三角形$${APQ}$$の外心であるとき
$${B, C, P, Q}$$が同一円周上にあることを示すのは非常に容易です。
このときの$${P, Q}$$以外に条件を満たす$${P, Q}$$のとり方がないことを示せれば、
題意を示すことができます。
やや裏技のようですが、図形問題を解くうえでは非常に有効なテクニックですので、
この問題をいい練習として習得すると良さそうです。
(同一法 と呼ばれる手法のようです。)
解答例:
$${HP = HQ = AH}$$を示せばよい。
$${P', Q'}$$を、$${A, B, P'}$$と$${A, C, Q'}$$がともにこの順位一直線上に並び、かつ$${HP' = HQ' = AH}$$となるようにとる。
$${\angle HAP' = \angle HP'A = \theta_1, \angle HAQ' = \angle HQ'A = \theta_2}$$
とおくと、$${\angle HP'Q' = 90^{\circ} - \theta_1 - \theta_2}$$であるから、
$${\angle AP'Q' = \theta_1 + 90^{\circ} - \theta_1 - \theta_2 = 90^{\circ} -\theta_2 = \angle ACB}$$より、
$${B, C, P', Q'}$$は同一円周上にある。

$${P, Q}$$と$${P', Q'}$$が異なる点だとして矛盾を示す。
$${AP < AQ}$$とする。
$${B, C, P, Q}$$が同一円周上にあることから、
$${\angle APQ = \angle ACB = \angle AP'Q'}$$であるため、
$${PQ}$$と$${P'Q'}$$は平行である。
よって対称性から$${\angle PP'H = \angle QQ'H}$$となるため、
$${\angle ACB = \angle AP'Q' = \angle AQ'P' = \angle ABC}$$となり、
$${AB = AC}$$となる。これは条件に反する。
$${AP > AQ}$$のときは、同様に対称性から
$${\angle P'PH = \angle Q'QH}$$
が得られ、
$${\angle ACB = \angle APQ = \angle AQP = \angle ABC}$$となり、
$${AB = AC}$$となり矛盾する。
よって、$${P', Q'}$$は$${P, Q}$$に一致するため、
$${HP = HQ = AH}$$となる。
三角関数を用いた解答例:
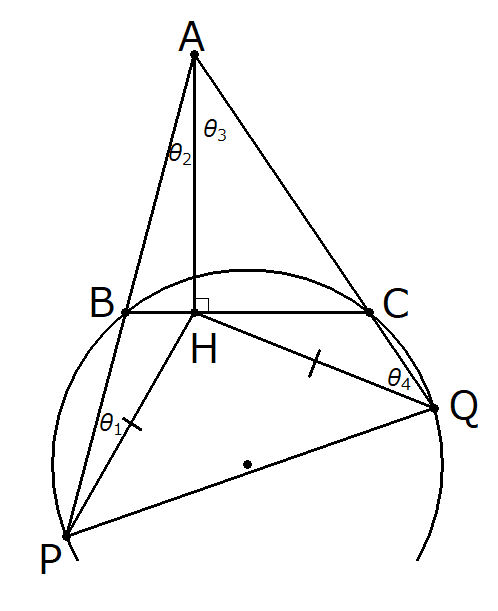
$${\angle APH = \theta_1, \angle PAH = \theta_2, \angle AQH = \theta_3, \angle QAH = \theta_4}$$とおく。
$${\angle PHQ = \theta_1 + \theta_2 + \theta_3 + \theta_4}$$
であるから、
$${\angle HPQ = 90^{\circ} - \frac{\theta_1 + \theta_2 + \theta_3 + \theta_4}{2}}$$
$${B, C, P, Q}$$が同一円周上にあるから、
$${\angle ACB = \angle APQ}$$であることより、
$${90^{\circ} - \theta_3 = \theta_1 + 90^{\circ} - \frac{\theta_1 + \theta_2 + \theta_3 + \theta_4}{2}}$$
よって$${\theta_1 + \theta_3 = \theta_2 + \theta_4}$$を得る。
さて、正弦定理より
$${\frac{AH}{\sin\theta_1} = \frac{HP}{\sin\theta_2}, \frac{AH}{\sin\theta_4} = \frac{HQ}{\sin\theta_3}}$$
であるから、これと$${HP = HQ}$$より
$${\sin\theta_1\sin\theta_3 = \sin\theta_3\sin\theta_4}$$
を得る。積を和に変換し
$${-\cos(\theta_1+\theta_3) + \cos(\theta_1 - \theta_3) = -\cos(\theta_2+\theta_4) + \cos(\theta_2 - \theta_4)}$$
となる。$${\theta_1 + \theta_3 = \theta_2 + \theta_4}$$であるから、
$${\cos(\theta_1 - \theta_3) = \cos(\theta_2 - \theta_4)}$$
となる。
$${-90^{\circ} < \theta_1 - \theta_3 < 90^{\circ}, -90^{\circ} < \theta_12- \theta_4 < 90^{\circ}}$$に注意すると、この式は
$${\theta_1 - \theta_3 = \pm(\theta_2 - \theta_4)}$$
となる。
よって$${\theta_1 = \theta_4, \theta_2 = \theta_3}$$
または$${\theta_1 = \theta_2, \theta_3 = \theta_4}$$となるが、
$${\theta_1 = \theta_4, \theta_2 = \theta_3}$$ は$${AB = AC}$$となり不適。
よって$${\theta_1 = \theta_2, \theta_3 = \theta_4}$$であり、
$${HP = HQ = AH}$$である。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
