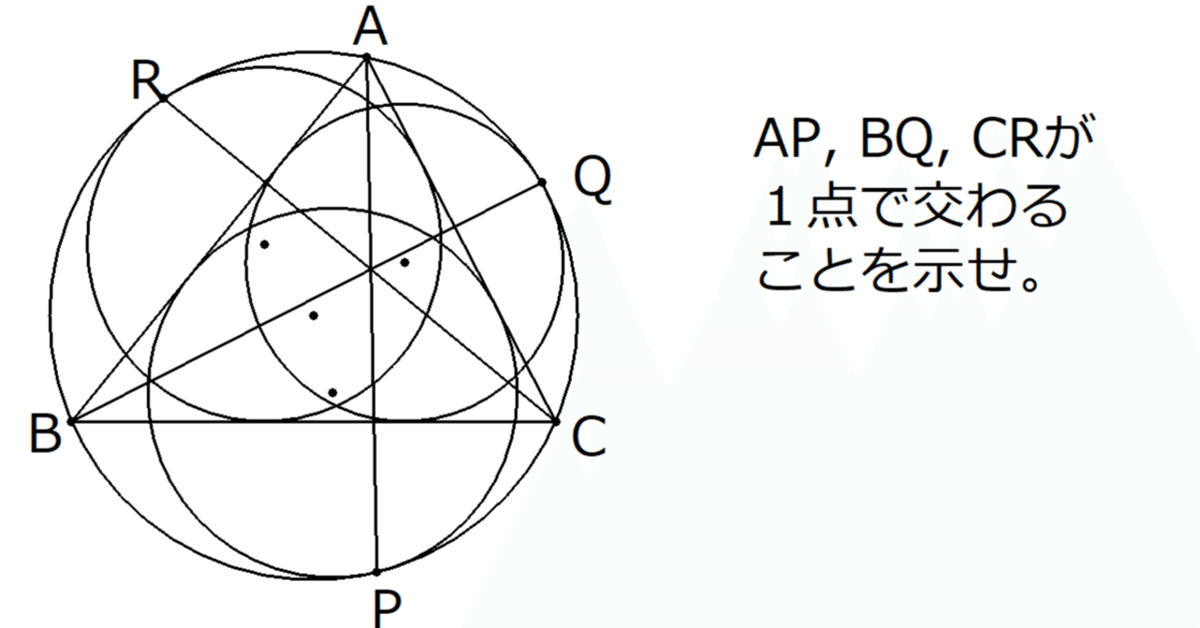
2007年 日本数学オリンピック本選 第3問 解答例
三角形$${ABC}$$の外接円を$${\varGamma}$$とする。辺$${AB, AC}$$に接し、$${\varGamma}$$に内接する円を$${\varGamma_A}$$、辺$${AB, BC}$$に接し、$${\varGamma}$$に内接する円を$${\varGamma_B}$$、辺$${AC, BC}$$に接し、$${\varGamma}$$に内接する円を$${\varGamma_C}$$とする。円$${\varGamma}$$と$${\varGamma_A, \varGamma_B, \varGamma_C}$$との接点をそれぞれ$${P, Q, R}$$とおく。
直線$${AP, BQ, CR}$$は一点で交わることを示せ。
考え方:
3直線が一点で交わることを示すのは大変で、初手に困る問題です。
問題としては対称性が高く、一点で交わることからチェバの定理の構図が見えるので、
チェバの定理の逆を使いたくなりました。
$${AP}$$と$${BC}$$の交点を$${X}$$とし、
相似関係を上手く利用して角度を追って、
$${BX:XC}$$を三角形のパラメータで上手く表すことができれば、
計算により乗り切れそうです。
解答例:
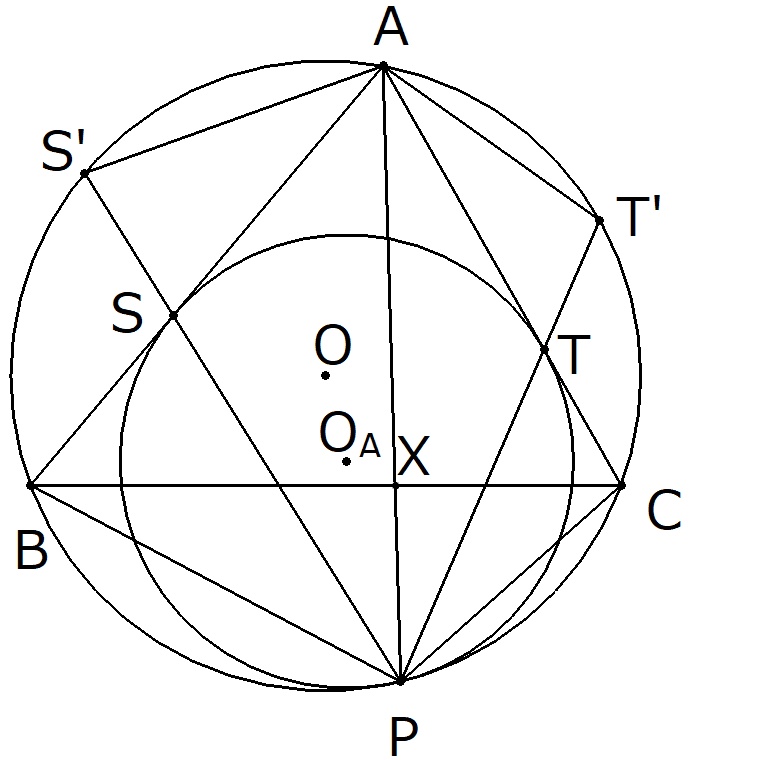
$${AP}$$と$${BC}$$の交点を$${X}$$とする。
また、$${\varGamma_A}$$と$${AB}$$の接点を$${S}$$、$${\varGamma_A}$$と$${AC}$$の接点を$${T}$$とする。
さらに直線$${PS}$$と$${\varGamma}$$との交点を$${S'}$$、
直線$${PT}$$と$${\varGamma}$$との交点を$${T'}$$とする。
また、$${\varGamma}$$の中心を$${O}$$とし、$${\varGamma_A}$$の中心を$${O_A}$$とする。
$${P, O, O_A}$$は同一直線上にあること、
$${PO_A = TO_A}$$および$${PO = T'O}$$、
三角形$${PO_AT}$$と三角形$${POT'}$$は相似である。
よって$${O_AT}$$と$${OT'}$$は平行であり、
$${OT'}$$と$${AC}$$は垂直である。
よって$${T'}$$は弧$${AC}$$を等分するから、
$${\angle APT' = \angle CPT' = \frac{\angle B}{2}}$$
同様にして
$${\angle APS' = \angle BPS' = \frac{\angle C}{2}}$$
である。
これより、三角形$${APT'}$$と三角形$${TPC}$$は相似であり、
三角形$${APS'}$$と三角形$${SPB}$$は相似になる。
また、$${PT:PT' = PO_A:PO = PS:PS'}$$であるから、
$${PS' : PT' = PS : PT}$$が成り立つ。
$${\angle BAP = \theta, \angle CAP = \phi}$$とする。
$${AS = AT}$$であるから、正弦定理より
$${PS:PT = AS \frac{\sin{\theta}}{\sin \frac{\angle C}{2}}:AT\frac{\sin{\phi}}{\sin{\frac{\angle B}{2}}}= \sin{\theta} \sin{ \frac{\angle B}{2}}:\sin{\phi} \sin{ \frac{\angle C}{2}}}$$
よって
$${BP : PC = \frac{PS \cdot PS'}{AP} : \frac{PT \cdot PT'}{AP} = (\sin{\theta} \sin{ \frac{\angle B}{2}})^2:(\sin{\phi} \sin{ \frac{\angle C}{2}})^2}$$
となるが、正弦定理より
$${BP:PC = \sin{\theta} : \sin{\phi}}$$であるから、
$${\sin{\theta} : \sin{\phi} = (\sin{ \frac{\angle C}{2}})^2:(\sin{ \frac{\angle B}{2}})^2}$$
さて、正弦定理より
$${BX:XC = AX \frac{\sin{\theta}}{\sin{\angle B}}: AX \frac{\sin{\phi}}{\sin{\angle C}}= \sin{\theta}\sin{\angle C} : \sin{\phi}\sin{\angle B}}$$
より、
$${\frac{BX}{XC} = \frac{\sin{\theta}\sin{\angle C}}{\sin{\phi}\sin{\angle B}} = \frac{\sin{\angle C} \sin^2{\frac{\angle C}{2}}}{\sin{\angle B}\sin^2{\frac{\angle B}{2}}}}$$
となる。
ここで、$${BQ}$$と$${CA}$$の交点を$${Y}$$とし、
$${CR}$$と$${AB}$$の交点を$${Z}$$ととすると、同じ議論により
$${\frac{CY}{YA} = \frac{\sin{\angle A} \sin^2{\frac{\angle A}{2}}}{\sin{\angle C}\sin^2{\frac{\angle C}{2}}}}$$
$${\frac{AZ}{ZB} = \frac{\sin{\angle B} \sin^2{\frac{\angle B}{2}}}{\sin{\angle A}\sin^2{\frac{\angle A}{2}}}}$$
となるので、
$${\frac{BX}{XC}\frac{CY}{YA}\frac{AZ}{ZB} = 1}$$
が成り立つ。
チェバの定理の逆より、$${AX, BY, CZ}$$は一点で交わり、
これにより題意が示された。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
