Pythonで学ぶ統計学６：最尤推定・MAP推定・ベイズ推定

１．概要

　本記事では今まで統計学の内容を元に「最尤推定・MAP推定・ベイズ推定」に関して記事を作成しました。

１－１．目的

　概要のまとめとしては下表の通りであり、これらを数式・コードも交えて説明します。今回は本・Youtube・Udemyでも見かけないほど詳細に書いているため有料としております。

１－２．対象者

　本記事の対象者は下記を想定しています。

• 確率、尤度、ベイズ統計の基礎を学びたい

• 今まで統計学の本・教材を読んできたのに理解できない、挫折した

• 確率、尤度、ベイズ統計を数式の羅列でなく意味を説明したうえで可視化された情報もみたい

• Pythonコードをいじって自分で動かすことで動作チェックしたい。

• 将来的に機械学習を勉強する上で基礎となる知識を学びたい

　Pythonコードを記載しておりますが出力結果は全て記載しているためPythonを使用しなくても問題ございません。使用したい方は下記から個別に学習お願いします。

Pythonライブラリ｜KIYO｜note

Pythonライブラリ（機械学習・AI）｜KIYO｜note

１－３．記号・用語一覧

　使用する記号・用語一覧は下記の通りです。

• 全事象$${\Omega}$$：試行において起こりうる全ての事象をまとめたもの。サイコロなら$${\Omega=\{1,2,3,4,5,6\}}$$となる。

• 事象Aの確率 $${P(A)}$$：事象Aが起こる確率

• 事象Aの余事象の確率 $${P(A^c)}$$：事象Aが起こらない確率

• 同時確率 $${P(A \cap B)}$$：事象Aと事象Bが同時に起こる確率

• 和集合の確率 $${P(A \cup B)}$$：事象Aまたは事象Bが起こる確率

• 条件付き確率 $${P(A|B)}$$：事象Bが起こった条件下で事象Aが起こる確率

• 独立な事象の定義 $${P(A \cap B) = P(A)P(B)}$$：事象Aと事象Bが独立であることを示す

• パラメータ $${\theta}$$：関数の出力を変化させる係数であり、機械学習でいう重み$${\bf w}$$やバイアス$${b}$$に相当するもの

• 確率分布 $${f(x|\theta)}$$：パラメータ$${\theta}$$における確率密度関数または確率質量関数

• 尤度 $${p(x|\theta)}$$：パラメータ$${\theta}$$における観測データxの発生確率（データの出現確率の尤もらしさ）

• 尤度関数 $${L(\theta|x)}$$：観測データxにおいてパラメータ$${\theta}$$の尤もらしさ（尤度）を関数化したもの。変数はパラメータ$${\theta}$$

• 最尤推定値 $${\hat{\theta}}$$：尤度関数が最大となる、つまりデータに対して最も尤もらしいパラメータ$${\theta}$$の値

• 事前分布 $${p(\theta)}$$：パラメータ$${\theta}$$の事前確率分布であり、データに対して経験則追加のための分布に該当

• 事後分布 $${p(\theta|x)}$$：尤度に事前分布を反映させた確率分布

２．確率

２－１．事象と余事象

　事象とは「ある条件下で生じた出来事・試行の結果から生じる事柄」となります。例として”コイントスをして表が出る事象”や”サイコロを振って2の目がでる事象”などがあります。

　全事象$${\Omega}$$とは、ある試行について起こりうる全ての事象をまとめたものでありサイコロの例では$${\Omega = \{1,2,3,4,5,6\}}$$となります。

　余事象$${\bar{A}}$$（または$${A^c}$$）とは、ある事象Aに対して「事象Aが起こらない事象」です。コイントスで事象Ａ：表が出る場合、余事象は裏が出る確率となります。

２－２．確率と確率空間の概要

　確率とはある事象が起こる可能性を示す指標であり、値が大きいほどその事象が起こりやすいと解釈されます。一般的には発生した事象に対して取りうる事象を割ることで計算できます。

$$
P(A)=\frac{Aの事象}{全事象}=\frac{A}{\Omega}
$$

２－３．確率の性質：コルモゴロフの公理

　確率には下記のような性質があります。
（出典１：東北大学 確率の基本的性質 Lecture 1）
（出典２：九州大学 確率論の基礎１ （事象と標本空間・条件付き確率））

【１．非負性】
　任意の事象Aに対して確率は必ず0以上、1以下になる。

$$
0 \leqq P(A) \leqq 1
$$

【２．加法性（確率の下方定理）】
　互いに排反な事象AとBに対して、確率の和は和集合となる（排反でない場合は積集合を除外）。なお互いに排反とは「同時に起こることがない」ことを意味しており、コインの表と裏がでる事象は互いに排反となります。

$$
P(A \cup B) = P(A) + P(B)
$$

【３．全確率の法則】
　サンプル空間Ω（全事象または標本空間）

$$
P(\Omega) = 1
$$

２－４．確率変数と確率分布

　確率変数とは「ある変数の値をとる確率が存在する変数」であり、確率分布とは「確率変数がとる値とその値をとる確率の対応表」です。
　参考としてサイコロとコイントスの例で確率分布表を作成しました。

[IN]
import pandas as pd

class HorizontalDisplay:
    def __init__(self, *args):
        self.args = args
        
    def _repr_html_(self):
        template = '<div style="display: left; float: left; padding: 10px;">{}</div>'
        return ''.join(template.format(arg._repr_html_()) for arg in self.args)

#例1
dices = [1, 2, 3, 4, 5, 6] # サイコロの目：確率変数
probabilities_dice = [1/6, 1/6, 1/6, 1/6, 1/6, 1/6] # 確率

#例2
coins = ['表', '裏'] # コインの目：確率変数
probabilities_coin = [1/2, 1/2] # 確率

df1 = pd.DataFrame({'確率変数': dices, '確率': probabilities_dice})
df2 = pd.DataFrame({'確率変数': coins, '確率': probabilities_coin})
HorizontalDisplay(df1, df2)

[OUT]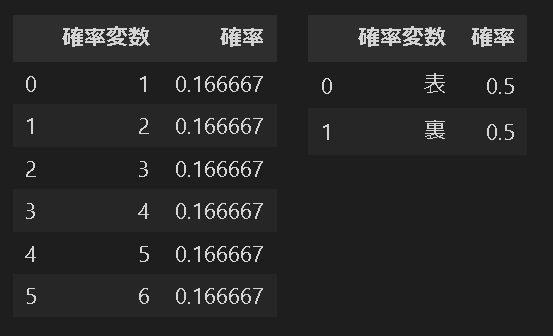

　関数$${p}$$に確率変数$${X}$$を渡すと確率$${p(X)}$$が出力される関数が作成でき、「確率変数$${X}$$ vs 確率$${p(X)}$$の分布」をとることができ、これを確率分布と呼びます。一般的に確率変数$${X}$$はサイコロのような離散値ではなく身長や年収のような連続値を取ります。
　確率変数$${X}$$が離散値の場合を「確率質量関数(pmf：probability mass function)」、連続値では「確率密度関数（PDF：probability density function)」と呼びます。

確率質量関数 - Wikipedia

２－５．確率分布の期待値と分散

　記述統計量で紹介した統計量と同様に、確率分布での統計量として期待値、分散を計算できます。

【確率質量関数（離散型データ）の場合】
　離散型における各項目の計算式は下記の通りです。なお$${X}$$は確率変数となります。

$$
確率質量関数p(x)=P(X=x)
$$

$$
期待値　\displaystyle E [X]=\sum_x x p(x)
$$

$$
分散Var(X) = E[(X-E(X))^2] = \sum_x (x-E(X))^2 p(x)
$$

【確率密度関数（連続型データ）の場合】
　連続型における各項目の計算式は下記の通りです。
なお$${X}$$：確率変数、$${x}$$：データの値、$${\mu}$$：平均値、$${E(X)}$$：期待値、$${\sigma^2}$$：分散、$${f(x)}$$：確率密度関数(確率変数vs確率密度)です。

$$
確率密度関数f(x)の特性：\int_{-\infty}^{\infty} f(x) dx = 1
$$

$$
\mu=E(X) = \int_{-\infty}^{\infty} x f(x) dx=\int_{-\infty}^{\infty} (データ値 \times 確率密度) dx
$$

$$
\sigma^2 = E[(X-E(X))^2] = \int_{-\infty}^{\infty} (x-E(X))^2 f(x) dx
$$

$$
別Ver：\sigma^2 = E[(X - \mu)^2] = \int_{-\infty}^{\infty} (x - \mu)^2 f(x) dx=\int_{-\infty}^{\infty} ((データ値 - 平均値)^2 \times 確率密度) dx
$$

３．条件付き確率・同時分布

３－１．条件付き確率の定義

　条件付き確率 $${P(A \mid B)}$$とは「与えられたある事象 $${B}$$ が起こったという条件のもとで、別の事象 $${A}$$ が起こる確率を表す確率」です（後述しますが同時確率とは別物です）。式は下記の通りです。

$$
P(A \mid B) = \frac{P(A \cap B)}{P(B)}
$$

$$
(B条件下におけるAの)条件付き確率=\frac{AとBの同時確率}{事象Bの確率}
$$

• 条件付き確率 $${P(A \mid B)}$$：$${B}$$ が起こった条件下の元で $${A}$$が起こる確率

• 同時確率 $${P(A \cap B)}$$（または$${P(A, B)}$$）： $${A}$$ と $${B}$$ が同時におこる確率

• $${P(A)}$$, $${P(B)}$$：事象$${A}$$ と 事象$${B}$$が生じる確率

３－２．条件付き確率と同時確率の違い

　条件付き確率と同時確率は概念が異なります。事象A, 事象Bで考えた時、条件付き確率$${P(B \mid A)}$$は事象A->事象Bの順における確率ですが、同時確率$${P(A \cap B)}$$はA・Bが同時に生じるのであれば順序は関係ありません。
　例として事象A：コイントスをしてから、事象B：サイコロを振る試行を考えてみます。事象Aが表の場合にサイコロが6となる条件付き確率$${P(B \mid A)}$$は（コイントスはサイコロに影響を与えないため）$${\frac{1}{6}}$$となります。しかし、同時確率$${P(A \cap B)}$$は事象Aで表が出た確率とサイコロの目が出る確率の両方が影響するため$${\frac{1}{12}}$$になります。
　前述の通り、「同時確率＝条件付き確率×その条件となる事象が生じる確率」で計算することが出来ます。

$$
P(A \cap B)=P(B \mid A) \times P(A)
$$

３－４．同時分布と周辺確率（周辺化）

　条件付き確率や同時確率において他にも多数の用語があります。まずは一覧を記載します。

• 同時確率（joint probability）$${P(X=x, Y=y)}$$：2つの事象（ここではXとY）が同時に起こる確率

• 同時分布 (joint distribution)$${P(X, Y)}$$：2つの変数（ここではXとY）が同時にどのような値を取るかに関する確率分布

• 周辺化 (marginalization)$${\sum_{y} P(X=x, Y=y)}$$：ある変数（ここではX）に関する確率を求めるために、他の変数（ここではY）について確率を合計する操作

• 周辺確率 (marginal probability)$${p(X=x) = \sum_{y} P(X=x, Y=y)}$$：周辺化によって得られた、ある変数（ここではX）の確率

• 周辺確率分布 (marginal probability distribution)$${p(X)}$$：周辺化によって計算された周辺確率の確率分布

• 条件付き確率 (conditional probability)$${P(Y=y|X=x)}$$：ある事象（ここではX）が起こったという条件のもとで、別の事象（ここではY）が起こる確率

• 条件付き分布(conditional distribution)$${P(Y|X)}$$：条件付き確率の分布

　それぞれの用語について事例を用いて紹介します。コイントスを２回する事象を考え１回目を$${X}$$, 2回目を$${Y}$$として、試行より下記結果が得られたとします。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
from typing import List

def count_cointoss(xs:List, ys:List):
    out_11, out_10, out_01, out_00 = 0, 0, 0, 0
    for x, y in zip(xs, ys):
        if x == 1 and y == 1:
            out_11 += 1
        elif x == 1 and y == 0:
            out_10 += 1
        elif x == 0 and y == 1:
            out_01 += 1
        elif x == 0 and y == 0:
            out_00 += 1
    return {'11': out_11, '10': out_10, '01': out_01, '00': out_00}

#コイントスの結果：表=1、裏=0
cointoss = np.array([[1, 1],
                    [1, 1],
                    [1, 1],
                    [1, 1],
                    [1, 0],
                    [1, 0],
                    [1, 0],
                    [0, 1],
                    [0, 1],
                    [0, 0]])

x, y = cointoss[:, 0], cointoss[:, 1]
df = pd.DataFrame({'表': x, '裏': y})
results = count_cointoss(x, y) #コイントスの結果を集計
count_11, count_10, count_01, count_00 = results['11'], results['10'], results['01'], results['00']
prob_11, prob_10, prob_01, prob_00 = count_11/len(cointoss), count_10/len(cointoss), count_01/len(cointoss), count_00/len(cointoss) #確率を計算

#プロットの可視化
fig, ax = plt.subplots(figsize=(5, 5), facecolor='w')
sns.scatterplot(x=r'表', y=r'裏', data=df, ax=ax, s=100, color='red', alpha=0.2, edgecolor='black')
#テキスト追加（事象数と確率)
ax.text(1, 0.9, f'表・表の回数: {count_11}', fontsize=10, ha='center', va='center') #表・表の回数
ax.text(1, 0.1, f'表・裏の回数: {count_10}', fontsize=10, ha='center', va='center') #表・裏の回数
ax.text(0.1, 0.9, f'裏・表の回数: {count_01}', fontsize=10, ha='center', va='center') #裏・表の回数
ax.text(0.1, 0.1, f'裏・裏の回数: {count_00}', fontsize=10, ha='center', va='center') #裏・裏の回数
ax.text(1, 0.8, r'$P(X=1, Y=1)$：' + f'{prob_11:.2f}', fontsize=10, ha='center', va='center') #表・表の確率
ax.text(1, 0.2, r'$P(X=1, Y=0)$：' + f'{prob_10:.2f}', fontsize=10, ha='center', va='center') #表・裏の確率
ax.text(0.16, 0.8, r'$P(X=0, Y=1)$：' + f'{prob_01:.2f}', fontsize=10, ha='center', va='center') #裏・表の確率
ax.text(0.16, 0.2, r'$P(X=0, Y=0)$：' + f'{prob_00:.2f}', fontsize=10, ha='center', va='center') #裏・裏の確率
plt.grid()
plt.show()


[OUT]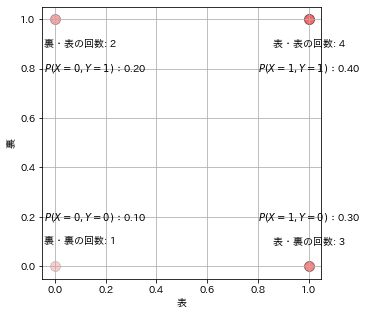

　今回のケースでは２回のコイントスのため1回目：$${X}$$, 2回目：$${Y}$$はこの試行では着目点を変えると下記の通り複数の確率が得られます(事象Xを先に実施する前提で記載しましたがYが先でも考え方は同じ)。

• $${X}$$と$${Y}$$が同時に結果x, yをとる確率：同時確率

• $${X=x}$$になった条件下で$${Y=y}$$をとる確率：条件付き確率

• $${Y}$$がどのような値をとるかに関わらず$${X=x}$$となる確率：周辺確率

　周辺確率とは周辺化（任意の変数に対して同時分布を総和すること）することで得られる確率であり、特定の事象に関する確率が得られます。それぞれの確率は以下の通りです。

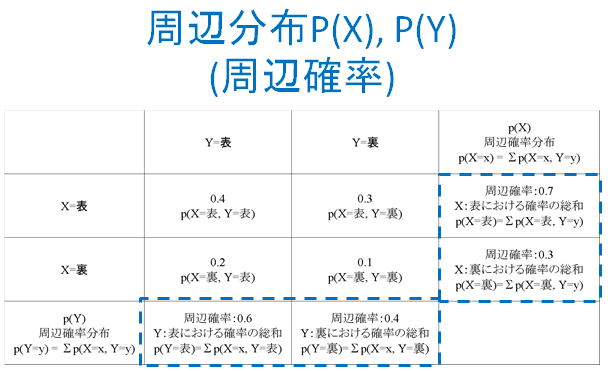
　上記の分布を条件付き確率に変換すると下記の通りです。$${\sum_y p(Y = y | X = x) = 1}$$となりますが、$${\sum_x P(Y = y | X = x)}$$は1出ないことに注意が必要です。

$$
条件付き確率の定義 P(B|A)=\frac{P(A,B)}{P(A)}
$$