<学習シリーズ>ガウス過程回帰とベイズ最適化
1.概要
1-1.緒言
本記事は”学習シリーズ”として「ガウス過程回帰(Gaussian Process Regression: GPR)」を紹介します。
本記事のまとめは下記の通りです。(製作期間2ヶ月以上ということもあり)一部の内容は有料にしております。本記事の対象者は下記を想定しています。出力は全て記載しているためPythonが使えなくても問題ないですが、次節の前提知識(特にベイズ推定)の理解は必須となります。
ガウス過程回帰やベイズ最適化を学びたい
ガウス過程回帰やベイズ最適化を本やブログで学習したけど挫折した
Pythonコードをいじって自分で動かすことで動作チェックしたい。
将来的に機械学習/マテリアルインフォマティクス(MI)を使用するため、基礎知識を学びたい
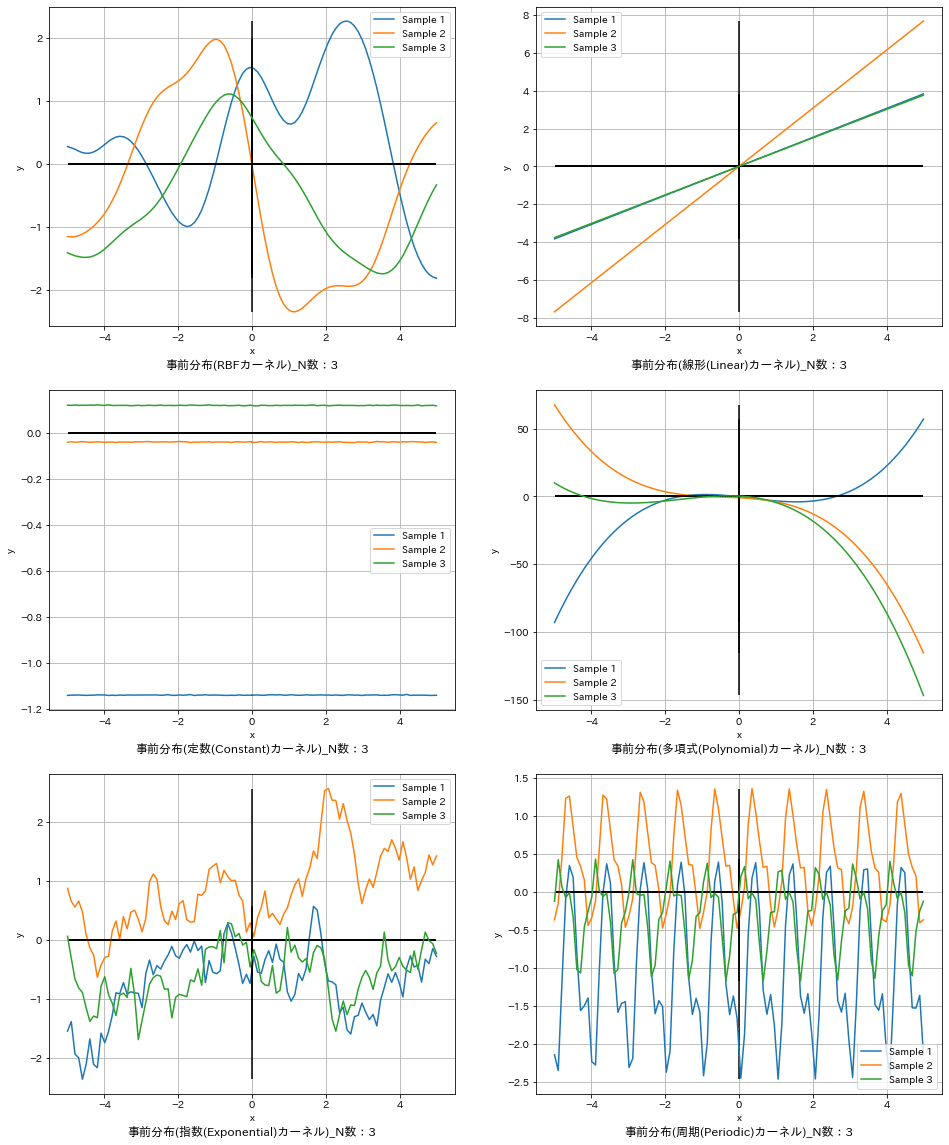
【事前分布】
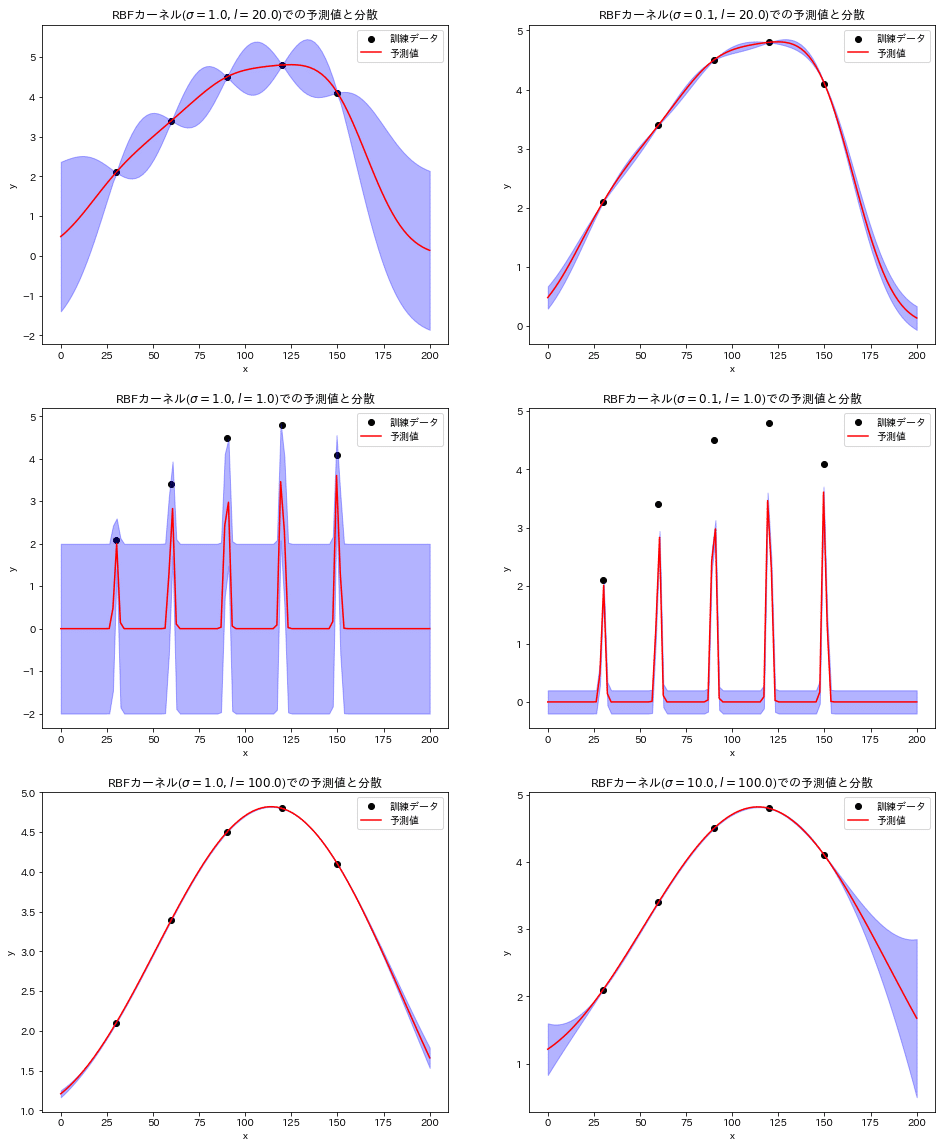
【事後分布】
【ベイズ最適化】

1-2.前提知識
ガウス過程回帰を理解する前に必要な前提知識は下記の通りです。
なお出力を切り替えできるように一部のコードにはloggingを使用しました。必要に応じて"logging.basicConfig(level)"を調整して、不要な情報を非表示にできます。
1-3.想定事例
本記事では理解しやすい事例としてコーヒーの抽出法を考えます。事例の数値は適当ですが、ガウス過程回帰/ベイズ最適化を理解したら自宅でも実験できるため、自分で最高のコーヒー抽出法を探索できると思います。

2.用語一覧
関連する用語および記号は下記の通りです。
2-1.全般
ガウス過程回帰で使用される用語は下記の通りです。
エントリ(行列成分:matrix entry):行列の中の個々の値を指します。例えば、3x3の行列では全体で9つのエントリが存在します。これは数学の一般的な用語であり、2行目3列目のエントリなどといったように行列の特定の位置の値を指す際に使います。
ガウス過程(Gaussian Process):ガウス分布や多変量ガウス分布を無限次元に拡張したものであり、関数のすべての可能な出力(すべての関数値)が共同でガウス分布に従うというアイデアを扱います。特定の入力値$${x}$$での関数$${f(x)}$$の出力をランダム変数と見なすことができます。
ガウス過程回帰:ガウス過程回帰とは関数の予測を行うための統計的手法の一つであり、ガウス過程という概念に基づいています。ガウス過程は、無数のランダムな変数が各々正規分布に従っていて、その組み合わせ全体が特定のパターンを持つ、という状態を表現します。ガウス過程回帰では、取得したデータ点全体から新たなデータ点の予測を行い、データの不確定性も考慮に入れた予測を可能にします。
目的関数:目的関数とは最適化問題で最小化または最大化しようとする関数のことです。つまり目的関数は「何を達成しようとしているか」を数学的に表現します。例えば、コーヒーの味を最良にするという目的がある場合はその「最良の味」を数値化し、それを最大化する関数が目的関数となります。
平均関数(Mean Function):ガウス過程回帰における平均関数は、データポイントの集まりから予測される平均値を提供します。
平均関数はデータの平均的な振る舞いをモデル化するため、結果的には我々が適合させようとする機械学習モデルとなります。
平均関数が線形(あるいは定数)であってもカーネル関数により非線形な関係性をモデル化できるため、結果として非線形なデータを推論することが可能になります。
分散関数(Covariance Function):分散関数は、ガウス過程回帰における予測の不確定性を提供します。つまり予測値がどれだけ信頼できるかを数値化します。
カーネル(カーネル関数:Kernel Function): カーネルは主に機械学習のコンテキストで使用され、データポイント間の類似性または距離を計算する関数を指します。カーネルは下記などがあります。
線形カーネル(linear kernel):$${k(x,x')=x^Tx'}$$ 2つのベクトル間のドット積(内積)を計算
指数カーネル(exponential kernel):$${k(x,x')=exp(-\frac{|x-x'|}{\theta})}$$
周期カーネル(periodic kernel):$${k(x,x')=exp(\theta_{1}cos(\frac{|x-x'|}{\theta_{2}}))}$$
ガウスカーネル:ガウスカーネルは指数カーネルの一種でありガウス過程で最もよく使用されるカーネルの一つです。二つの入力間の類似度を計算し値は0から1の範囲であり、1は完全に一致する場合、0は全く関連性がない場合を示します。
動径基底関数(Radial Basis Function:RBF)カーネルとも呼ばれます
カーネル行列:カーネル行列はすべての訓練データポイント間のカーネル関数の値を含む行列です。
3つのデータ点がある場合はカーネル行列は3x3の行列になり、各エントリは対応するデータ点間のカーネル関数の値を示します。
カーネル行列は「学習データ間のカーネル関数の値を格納した行列」であり、分散共分散行列は「特徴量の分散と共分散を格納した行列」であり、異なる点があります。
Φのグラム行列とも呼ばれます。
グラム行列:$${n}$$個のベクトル$${(v_1, v_2, \cdots v_n)}$$の内積を各成分に持つ次の行列をグラム行列 (Gram matrix) と言います。
予測値/予測分散:予測値は”新しい入力に対する目的関数の予測値”で、予測分散は”その予測の不確実性”を表します。
信頼区間:信頼区間とは統計的推定の不確定性を表すための範囲です。例えば、平均値の予測があっても正確にその値であることは保証できません。そのため、その予測値を中心として一定の範囲を設け、その範囲内に真の値が含まれる確率を指定します。その範囲が信頼区間となります。
獲得関数(Acquisition Function):獲得関数はベイズ最適化において次に試すべきデータポイント(次に試すべき試験条件)を決定するための関数です。この関数は予測値の期待値と不確定性を同時に考慮し、探索と利用のバランスを取ることで最適な次の試行を選びます。獲得関数にはEI, PI, UCB/LCBなどがあります。
ベイズ最適化: ベイズ最適化はある関数(e.g. 機械学習モデルの精度を向上させるハイパーパラメータ)を最適化するための手法です。これはブラックボックス関数の最適化問題に対する一つのアプローチで、ガウス過程と呼ばれる確率的モデルを用いて関数を近似し、次に評価すべき点を選択するために獲得関数を用います。
標準正規分布の累積分布関数$${\Phi}$$:累積分布関数$${\Phi}$$は、標準正規分布の確率密度関数を(負の無限大から指定した$${x}$$まで)積分したものであり、「ある値$${x}$$までの確率」を表します。
標準正規分布の確率密度関数$${\phi}$$:確率密度関数$${\phi}$$は、標準正規分布(平均0、標準偏差1の正規分布)の形状を表す関数であり、ある値た$${x}$$を取る確率を表します。
基底関数:ある関数空間(ベクトル空間)の基底(基本要素)を形成する関数のことを指します。線形代数における「基底」の概念と同様ですが、ここでは関数が対象となります。
多項式の場合、基底関数は$${x^0, x^1, x^2, \dots}$$となります。
計画行列(デザイン行列):線形回帰分析などの統計モデルで用いられる行列で、各行が一つの観測値、各列が一つの説明変数(特徴量)を表します。この行列を用いて線形結合(内積)を取ることでモデルの出力(予測値)を計算します。
ある本では「計画行列$${Φ}$$は「基底関数$${φ_j(x_n)}$$を$${N}$$行$${M}$$列に並べたもの」と表現しているみたいです。
2-2.獲得関数の紹介
ベイズ最適化において次に試すべき試験条件を決定する獲得関数には以下のようなものがあります。注意点として一部の獲得関数にはハイパーパラメータ(分析者が手動で設定する必要があるパラメータ)があり、値次第で得られる結果が変わります。
Expected Improvement(期待改善量:EI):EIは現在の最善の目的関数値を改善するための期待値を最大化しようとする獲得関数です。EIは初めての評価や探索中に、まだ試していないパラメータの組み合わせを探すのに特に有効です。一方で評価が進むとともに現在の最善の結果を改善する余地が少なくなり、最適化は停滞する可能性があります。
Probability of Improvement (改善確率:PI):PIは改善の確率を最大化しようとする獲得関数です。つまり新たに試すパラメータの組み合わせが現在の最善の結果を改善する確率を最大にするものを選びます。PIは概念的には非常にシンプルですが、改善の確率だけを追求するため小さな改善しか見込めない領域に引きつけられる傾向があります。
信頼性上限関数UCB(Upper Confidence Bound):UCBは探索(不確実性)と利用(予測値)のバランスをとるための獲得関数です。ハイパーパラメータによって、このバランスを調整することができます。一般的には探索が必要な初期段階では探索を重視し、次第に利用に重きを置くように調整します。これにより評価を進めるとともに領域の全体的な特性を理解し、最適化を進めることができます。
信頼性下限関数LCB(Lower Confidence Bound):UCBと最小値Ver.
Thompson Sampling(Stochastic sampling):Thompson Samplingは確率的な獲得関数であり、現在の予測分布からサンプリングを行い、そのサンプルが最大となるデータポイントを選びます。
2-3.数式一覧
【カーネル】
ガウスカーネル(RBFカーネル、指数二乗カーネル)
ガウスカーネル関数(またはRBF:Radial basis function kernel)は$${x}$$と$${x'}$$が近い時(入力データが似ている)には大きな値を返し、$${x}$$と$${x'}$$が遠い時(入力データが似ていない)には小さな値を返します。つまりこのカーネル関数はデータ同士の類似性を表現します。
$$
k(\bf x, \bf x') = \theta_1\exp\left(-\frac{||\bf x - \bf x'||^2}{\theta_2}\right)
$$
$${\theta_1, \theta_2}$$:カーネル関数の性質を決めるパラメータ
【カーネル行列】
カーネル行列の要素は$${K_{ij} = k(x_i, x_j)}$$
$$
K = \begin{bmatrix} k(x_1, x_1) & k(x_1, x_2) & \cdots & k(x_1, x_n) \\
k(x_2, x_1) & k(x_2, x_2) & \cdots & k(x_2, x_n) \\
\vdots & \vdots & \ddots & \vdots \\
k(x_n, x_1) & k(x_n, x_2) & \cdots & k(x_n, x_n)
\end{bmatrix}
$$
【予測値/予測分散】
$$
f_* = k(x_*, X)K^{-1}y
$$
$$
v_* = k(x_, x_) - k(x_, X)K^{-1}k(X, x_)
$$
【獲得関数】
EIを最大化する$${x}$$を求めると次に試すべき試験条件が決定します。
$$
EI(x) = (y(x) - y(x^+))\Phi(Z) + \sigma(x)\phi(Z)
$$
$${\mu(x)}$$:予測分布の平均
$${\sigma(x)}$$:予測分布の標準偏差
$${f(x^+)}$$:これまでの評価の最大値
$${\xi}$$:探索と活用のバランスを調整するハイパーパラメータ
$${\Phi(Z)}$$:標準正規分布の累積分布関数
$${\phi(Z)}$$:標準正規分布の確率密度関数
$$
PI(x) = \Phi \left( \frac{y(x) - y(x^+)}{\sigma(x)} \right)
$$
$$
UCB(x) = y(x) + k \sigma(x)
$$
$$
LCB(x) = y(x) - k \sigma(x)
$$
【重回帰モデル$${\mathbf{\hat y}=\mathbf{X} \mathbf{w}}$$】
$${\mathbf{\hat y}}$$:推論値、 $${\mathbf{X}}$$:計画行列(design matrix)、 $${\mathbf{w}}$$:重み
$$
\underbrace{\begin{bmatrix}\hat y_1 \\\hat y_2 \\\hat y_3 \\\vdots \\\hat y_N
\end{bmatrix}}_{\mathbf{\hat y}}
= \underbrace{\begin{bmatrix}
x_{11} & x_{12} & x_{13} & \dots & x_{1M} \\
x_{21} & x_{22} & x_{23} & \dots & x_{2M} \\
x_{31} & x_{32} & x_{33} & \dots & x_{3M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N1} & x_{N2} & x_{N3} & \dots & x_{NM}
\end{bmatrix}}_{\mathbf{X}}
\underbrace{\begin{bmatrix}w_1 \\w_2 \\w_3 \\\vdots \\w_M
\end{bmatrix}}_{\mathbf{w}}
$$
【基底関数を用いた線形回帰モデル$${\mathbf{\hat y}=\mathbf{\Phi} \mathbf{w}}$$】
注意点として基底関数$${\phi(\bf x)}$$で使用した$${\mathbf{x}}$$はベクトル(データ全体)であり、$${x}$$の1つの要素ではありません。よって重回帰での列の次元数の記号は変えています。
$$
\underbrace{\begin{bmatrix}\hat y_1 \\\hat y_2 \\\hat y_3 \\\vdots \\\hat y_N
\end{bmatrix}}_{\mathbf{\hat y}}
= \underbrace{\begin{bmatrix}\phi_{0}(\mathbf{x_{1}}) & \phi_{1}(\mathbf{x_{1}}) & \phi_{2}(\mathbf{x_{1}}) & \dots & \phi_{H}(\mathbf{x_{1}}) \\\phi_{0}(\mathbf{x_{2}}) & \phi_{1}(\mathbf{x_{2}}) & \phi_{2}(\mathbf{x_{2}}) & \dots & \phi_{H}(\mathbf{x_{2}}) \\ \phi_{0}(\mathbf{x_{3}}) & \phi_{1}(\mathbf{x_{3}}) & \phi_{2}(\mathbf{x_{3}}) & \dots & \phi_{H}(\mathbf{x_{3}}) \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \phi_{0}(\mathbf{x_{N}}) & \phi_{1}(\mathbf{x_{N}}) & \phi_{2}(\mathbf{x_{N}}) & \dots & \phi_{H}(\mathbf{x_{N}})\end{bmatrix}
}_{\mathbf{\Phi}}
\underbrace{\begin{bmatrix}w_1 \\w_2 \\w_3 \\\vdots \\w_H
\end{bmatrix}}_{\mathbf{w}}
$$
2-4.Pythonライブラリの準備
Pythonで色々実装するための準備として関連するライブラリを事前にインポートします。不足している分は記事で適宜追加します。
[IN]
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
import scipy.stats as stats
import sympy as sym
import os, glob, datetime, re, time, itertools, json, japanize_matplotlibなおベイズ統計学に便利なライブラリ一覧は下記記事に記載しております。
3.ガウス過程の概要
3-1.ガウス過程回帰とは
ガウス過程回帰(Gaussian Process Regression:GPR)とは機械学習の一つであり、観測データを元に連続値を予測する手法です。基本的にはガウス過程を利用して観測データ間の関係を捉えて新たなデータ点の予測値を出力します。
GPRの特徴は以下の通りです。
非線形での回帰推論:主に回帰向けであり入力変数$${x}$$から出力変数$${y}$$を関数$${y=f(x)}$$を用いて推定できる。非線形であり複雑なデータにも対応可能
不確実性の量化:ベイズ推定を用いており、モデルは関数分布として得られるため推定の不確実性(標準偏差)を表現できる。
パラメータ計算の性質:深層学習のような学習(誤差逆伝搬)はなくモデルは一意に決まる。ただし得られる出力は事後分布であり、関数は事後分布からランダムに抽出するため不確実性が表現される。
計算の複雑さ:大きなデメリットとしては、計算が複雑であり訓練データセットのサイズが大きい場合はガウス過程の計算(特にカーネル行列の逆行列の計算)に時間がかかる可能性があります(計算量$${O(N^3)}$$)。
カーネル関数の性質と選定:カーネル関数を選択することにより、どの程度の複雑さや滑らかさをモデルに組み込むかを制御することができます。ただし、正しいカーネル関数を選択するには経験や試行錯誤が必要です。
多次元データへの難しさ:多次元になると次元の呪いにより、他のモデルより予測性能が低下する可能性があります。
ガウス過程回帰の用途としてシミュレーションやベイズ最適化によるマテリアルズ・インフォマティクス(MI)での新規材料の探索などがあります。
面白い事例としてGoogleでは「The makings of a smart cookie」としてベイズ最適化を用いたクッキー調理法の最適化を実施しています(論文:Bayesian Optimization for a Better Dessert)。
【参考資料】
【コラム:マテリアルズ・インフォマティクス(MI)とは?】
MIとはAIや機械学習を用いて製品組成(ガラス、バッテリーなど)や触媒合成条件を探索する手法です。今までは研究者の直感と経験則で進めてきた開発をAIにすることで、より再現性高く・高速・安価に開発を進めることが出来ると期待されます。歴史の概要は下記の通りです.
2011年:米国で世界的なMIブームの先駆けとなるMaterials Genome Initiative (MGI)がオバマ大統領(当時) の主動で 2011 年から開始した。
2012年:韓国サムスンとMITがMIを用いて全固体電池の新規材料を1年という短期間で開発した。この組成はトヨタは2011年5月に特許出願していたものと同等であり、MITからの発表は2012年10月であったため先に公開された。2012年11月にトヨタは特許権を取得できたが、開発が遅れていたら新規性がなくなり特許出願できなかった可能性もあった。
2015 年:欧州では European Center of Excellence の一環と して Novel Materials Discovery (NOMAD)が開始した。
(出典:材料開発の新潮流 ~マテリアルズインフォマティクス~)
3-2.ガウス過程とは
ガウス過程(Gaussian Process:GP)とは「無限次元のガウス分布」表します。具体的には任意の有限な点集合に対する値が多次元ガウス分布に従うものを指します。実際の観測/実験データは有限のため有限次元の多変量ガウス分布として扱われます。
ガウス過程は平均関数:$${m(x)}$$と共分散関数(またはカーネル関数):$${k(x, x')}$$を用いて以下の式で定義されます。
$$
f(x) \sim GP(m(x), k(x, x'))
$$
ガウス過程回帰では「観測データに基づいてガウス過程の平均関数:$${m(x)}$$と共分散関数:$${k(x, x')}$$を更新することでデータに適合した関数の分布を作成」します。具体的には観測データを用いて事後分布を計算し、その事後分布を新たな平均関数と共分散関数としてガウス過程を更新します。つまり、GPRはベイズ推論の一種と言えます。
3-3.ベイズ推論とは
ベイズ推論(Bayesian inference)とは確率的な推論の一種であり、観測データと事前の知識(事前分布)を組み合わせて事後分布を求める手法であり以下のベイズの定理に基づいています。
$$
事後分布P(\theta | D)
= \frac{P(D | \theta) P(\theta)}{P(D)}
= \frac{事前分布 \times 尤度関数}{データの確率(正規化項)}
$$
$${D}$$:データ、$${\theta}$$:パラメータ(GPRでは関数)
ベイズ推論ではデータが新しく観測されるたびにそれまでの事後分布を新たな事前分布とみなし、観測データから事後分布を更新できます。これをベイズ更新と言います。
ベイズ更新により、観測データが増えるごとに事後分布が改善され不確実性を適切に扱うことができます。
ガウス過程回帰では、関数の事前分布は平均関数とカーネル行列によって定義されるガウス過程であり、尤度関数は観測データと関数値の差(ノイズを含む)に基づきます。これらをベイズの定理に基づいて組み合わせることで、関数の事後分布(新しい平均関数と共分散関数)を得ます。よって、ガウス過程回帰はベイズ推論の枠組みを用いた手法と言えます。
【コラム:ベイズ推定とは】
ベイズ推定は事後分布からパラメータの最適値(事後平均、MAP推定値など)を求める手法であり、ベイズ推論の結果から具体的なパラメータの推定値を得るプロセスと言えます。
ガウス過程回帰では特定のパラメータ推定ではなく関数値の分布(事後分布)を予測することが主な目的となります。
4.平均関数と分散関数
「ガウス過程とは無限次元のガウス分布」を表すと言えます。
多変量ガウス分布では、分布を特徴づける重要な要素として「平均値ベクトル$${\bf \mu}$$:分布の重心」と「共分散行列$${\bf \Sigma}$$:分布の広がり・形状」の2つがあります(詳細は次節参照)。
$$
p(x)=f(x;μ,Σ) = \frac{1}{\sqrt{(2\pi)^{n}|\Sigma|}}\exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right)
$$
同様にガウス過程回帰でも”関数の分布”を決めるための要素として以下2つが重要となります。
平均関数:$${m(\bf x)}$$
分散関数:$${k(\bf x,\bf x')}$$
4-1.平均関数
ガウス過程における平均関数$${m(x)}$$は、入力$${x}$$の集合に対する「関数の期待値」を表します。
学習前の何も知らない状態では、事前分布を定数関数として扱い$${m(x) = 0}$$としたりします。もしドメイン知識や経験則があればその値を平均関数を選ぶこともあります。
ガウス過程回帰では、平均関数は初期の"推測"として働き、その後の観測データに基づくベイズ更新を通じて、最終的な関数の形状が決定されます。
4-2.共分散関数
共分散関数(カーネル関数)$k(x, x')$は、任意の2つの入力$${x}$$と$${x'}$$に対する関数値の相関を定義します。直観的にカーネル関数は2つの入力データ点間の「類似性」を測る役割を果たします。入力が互いに類似(空間的に近い)であるほど、それらの関数値も類似していると期待されます。
カーネル関数の選択はガウス過程の性質を大きく影響し、線形であったり滑らかな曲線であったり、周期性を持ったカーブを作成できたりします。カーネル関数は一般的にはハイパーパラメータ(分析者が手動で調整する変数)を持ち、最尤法(尤度関数の最大化)またはベイズ的な方法(事後分布の最大化)によって調整されます。
ガウス過程回帰では、観測データを用いてカーネル関数のパラメータが調整され、その結果得られる関数の事後分布はデータとカーネル関数の形状に適応します。
5.カーネル関数とカーネル行列
5-1.カーネル関数とは
カーネル関数は「2つのデータ点間の類似度」を計算するための関数であり、ガウス過程における共分散関数として使用されます。
カーネル関数は計算の容易性や特定の性質(例えば、滑らかさや周期性)を持つ関数をモデル化する能力などガウス過程の性質に影響を与えます。ガウス過程ではカーネル関数は$${k(x, x')}$$と定義され$${x}$$, $${x'}$$は入力データとなります。
5-2.カーネル行列(Φのグラム行列)とは
ガウス過程におけるカーネル行列(または$${Φ}$$のグラム行列)は全てのデータ点間の共分散(類似度)を表します。具体的には$${N}$$個のデータ点に対するカーネル行列$${K}$$は$${N×N}$$行列となり、$${K}$$の$${(i,j)}$$要素$${K_{ij}}$$はカーネル関数$${k(\bf x_i, \bf x_j)}$$の値となります。
※注意点としてデータ点$${\bf x}$$は全次元を含む配列であり、スカラー(個別の要素)ではありません。
$$
説明変数X=
\begin{bmatrix}
x_{11} & x_{12} & x_{13} & \dots & x_{1M} \\
x_{21} & x_{22} & x_{23} & \dots & x_{2M} \\
x_{31} & x_{32} & x_{33} & \dots & x_{2M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N1} & x_{N2} & x_{N3} & \dots & x_{NM}
\end{bmatrix}
=\begin{bmatrix}\mathbf{x}_1 \\\mathbf{x}_2 \\\mathbf{x}_3 \\
\vdots \\\mathbf{x}_N
\end{bmatrix}
$$
$$
カーネル行列K =
\begin{bmatrix}k(\mathbf{x}_1, \mathbf{x}_1) & k(\mathbf{x}_1, \mathbf{x}_2) & k(\mathbf{x}_1, \mathbf{x}_3) & \dots & k(\mathbf{x}_1, \mathbf{x}_N) \\
k(\mathbf{x}_2, \mathbf{x}_1) & k(\mathbf{x}_2, \mathbf{x}_2) & k(\mathbf{x}_2, \mathbf{x}_3) & \dots & k(\mathbf{x}_2, \mathbf{x}_N) \\k(\mathbf{x}_3, \mathbf{x}_1) & k(\mathbf{x}_3, \mathbf{x}_2) & k(\mathbf{x}_3, \mathbf{x}_3) & \dots & k(\mathbf{x}_3, \mathbf{x}_N) \\\vdots & \vdots & \vdots & \ddots & \vdots \\k(\mathbf{x}_N, \mathbf{x}_1) & k(\mathbf{x}_N, \mathbf{x}_2) & k(\mathbf{x}_N, \mathbf{x}_3) & \dots & k(\mathbf{x}_N, \mathbf{x}_N)
\end{bmatrix}
$$
”観測データ点”と”新規データ点”との間のカーネル行列を用いて新規データ点に対する予測を計算するため、カーネル行列はガウス過程の計算において重要な役割を果たします。
5-3.カーネル関数の種類
ガウス過程でのカーネル関数$${k(\bf x,\bf x')}$$が複数あり、それぞれが異なる性質の関数をモデル化する能力を持ちます。以下にいくつかの代表的なカーネル関数を紹介します。
5-3-1.ガウスカーネル(RBFカーネル)
ガウスカーネル(動径基底関数カーネル:Radial Basis Function)は最も一般的に使用されるカーネル関数の一つであり、滑らかで連続的な関数をモデル化する能力を持ち、以下のように定義されます。
$$
\begin{aligned}
k(x, x') &= \sigma^2\exp(-\frac{||x - x'||^2}{2l^2}) \\
&=\sigma^2\exp\left(-\frac{1}{2l^2}\sum_{i=1}^{M} (x_i - x'_i)^2\right)
\end{aligned}
$$
$${||\mathbf{x} - \mathbf{x'}||^2}$$:2つのデータ点間のユークリッド距離
$${\sigma^2}$$:出力の分散(全体的な関数のスケール)
$${l}$$:長さスケール(データ点がどれだけ離れていると関連性が失われるかを示すパラメータ)
【RBFカーネルでの類似性を可視化】
RBFカーネルの場合は”類似度=距離”であることを可視化しました。
RBFカーネルの数式を見ると正規分布と同形状であることが確認でき、$${x'}$$を中心に左右対称の釣り鐘カーブであることが分かります。そこで$${x'=0}$$としてRBFカーネルを描写したうえで、$${x=1, 3}$$の値(類似度)がどのように変化するかを計算しました。
結果として$${x'=0}$$から遠くなるほど指数関数的にカーネル値(類似度)が低下しています。これは正規分布が平均値から離れるほど確率密度が小さくなるのと同じ現象です。
また正規分布と同様に長さスケール$${l}$$(正規分布では標準偏差$${\sigma}$$)が分布の形状を変えるため、$${l}$$が大きくなると分布がブロードになりより遠い値でも似たような類似性を出力するようになります。
ガウス過程回帰においてカーネル関数のパラメータは分散度に依存するため調整が必要となります。
[IN]
def rbf_kernel(x1:float, x2:float, sigma:float, l:float):
return sigma**2 * np.exp(-(x1 - x2)**2 / (2 * l**2))
x = np.linspace(-5, 5, 100)
y_11 = rbf_kernel(x1=x, x2=0, sigma=1, l=1)
y_13 = rbf_kernel(x1=x, x2=0, sigma=1, l=3)
y_half3 = rbf_kernel(x1=x, x2=0, sigma=0.5, l=3)
x_0 = 0.0
x_1 = 1.0
x_3 = 3.0
print(f"x=0とx'=1のカーネル値: {rbf_kernel(x_0, x_1, 1, 1):.3f}")
print(f"x=0とx'=3のカーネル値: {rbf_kernel(x_0, x_3, 1, 1):.3f}")
sns.lineplot(x, y_11, label=r"RBF kernel: $\sigma=1, l=1$")
sns.lineplot(x, y_13, label=r"RBF kernel: $\sigma=1, l=3$")
sns.lineplot(x, y_half3, label=r"RBF kernel: $\sigma=\frac{1}{2}, l=3$")
sns.scatterplot([x_0], [0], label=r"$x'=0$", color='red')
sns.scatterplot([x_1, x_3], [0, 0], label=r"$x=1, 3$", color='blue')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0, fontsize=12), plt.grid()
plt.show()[OUT]
x=0とx'=1のカーネル値: 0.607
x=0とx'=3のカーネル値: 0.011
5-3-2.線形カーネル
線形カーネルは線形関係をモデル化します。式の通り、これは二つのデータ点の内積を取ることに相当します。
$$
k(x, x') = x^T x'
$$
【コサイン類似度との違い】
コサイン類似度とは「内積を用いて2本のベクトルのなす角のコサインを計算」することで類似度を表現する手法です。つまり「2本のベクトルがどれくらい同じ向きを向いているのかを表す指標」とも言えます。
数式は下記の通りです。線形カーネルとの差は分母の”ベクトルの大きさ(ノルム)”によるスケーリング項です。
$$
\cos(\theta) = \frac{x^T \cdot x'}{\|x\|\|x'\|}
$$
つまりコサイン類似度は「ベクトルの大きさは無視してベクトルの方向性のみ重視」しているのに対して、線形カーネルはベクトルの大きさも考慮している点が異なります。
5-3-3.指数カーネル
指数カーネルは特定の方向の差異を強調することができます。特定の方向に対する入力値の差が大きくなるほど、出力される値は小さくなります。数式で表すと以下のようになります。
$$
k(x, x') = \exp(-\frac{||x - x'||}{\theta})
$$
5-3-4.周期カーネル
周期カーネルは周期的なパターンをもつ関数をモデル化するのに適しています。
$$
k(x, x') = \exp(-\theta_1cos(\frac{||x - x'||}{\theta_2}))
$$
6.計画行列と基底関数
ガウス過程回帰ではデータ点間の類似性を表すためにカーネル関数(または共分散関数)を使用しました。ガウス過程回帰において、計画行列と基底関数はカーネル関数の計算に重要な役割を果たします。
具体的には基底関数を用いてデータ点を変換(特徴空間へのマッピング)した後、その変換されたデータ点間の類似性をカーネル関数を用いて測定します。計画行列はその変換結果を一括で扱うための行列で、これを用いてカーネル関数の計算を効率的に行うことが可能になります。
6-1.計画行列
計画行列(デザイン行列)とは、予測モデルを構築するために使用するデータセットを格納した行列です。一般的には各行が各データ点、各列が特徴量(次元)を表す形式になります。
なお計画行列の最初の列はバイアス項(定数項)として1を持つのが一般的です。
$$
X=
\begin{bmatrix}
x_{11} & x_{12} & x_{13} & \dots & x_{1M} \\
x_{21} & x_{22} & x_{23} & \dots & x_{2M} \\
x_{31} & x_{32} & x_{33} & \dots & x_{2M} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
x_{N1} & x_{N2} & x_{N3} & \dots & x_{NM}
\end{bmatrix}
$$
$${N}$$:データ点数
$${M}$$:特徴量の数(次元数)
$${1}$$:バイアス項(定数項)
6-2.基底関数
基底関数$${\phi}$$とは”データを変換するための関数”であり、データに非線形性を導入することでより柔軟なモデルを構築できるようにします。具体的には、基底関数を使用して入力変数をより高次元/非線形空間へとマッピングします。
下記に説明変数$${X}$$の入力データ$${\bf x_i}$$を基底関数$${\phi(x)}$$で写像して得られた新しい計画行列$${\Phi}$$を記載します。
$$
計画行列\Phi = \begin{bmatrix}\phi(x_{1})^T\\
\phi(x_{2})^T\\
\vdots\\
\phi(x_{N})^T\end{bmatrix}
= \begin{bmatrix}
\phi_{1}(x_{1}) & \phi_{2}(x_{1}) & \cdots & \phi_{M}(x_{1})\\
\phi_{1}(x_{2}) & \phi_{2}(x_{2}) & \cdots & \phi_{M}(x_{2})\\
\vdots & \vdots & \ddots & \vdots\\
\phi_{1}(x_{N}) & \phi_{2}(x_{N}) & \cdots & \phi_{M}(x_{N})\end{bmatrix}
$$
具体的な基底関数の例として多項式回帰での多項式基底関数があります。多項式回帰は線形回帰を一般化し特徴の高次の項を導入することでデータの非線形のパターンを捉えることができます。
7.GPR理解1:事前分布
ガウス過程回帰の事前分布の説明および実装を行います。事前分布とはデータを学習する前の関数やパラメータの分布です。
事前分布の基礎知識は下記記事をご確認ください。
説明用のために可視化用関数を事前に作成しました。
[IN]
def plot_data(ax, x, y, label:str, graph:str='plot', color:str=None, title:str=None, verbose:bool=False):
if verbose:
x_max, x_min, y_max, y_min = np.max(x), np.min(x), np.max(y), np.min(y)
ax.hlines(0, x_min, x_max, color='black', linestyle='solid')
ax.vlines(0, y_min, y_max, color='black', linestyle='solid')
if graph == 'plot':
ax.plot(x, y, color=color, label=label)
elif graph == 'scatter':
ax.scatter(x, y, color=color, label=label)
else:
raise ValueError('graphは"plot"か"scatter"を指定してください')
ax.set(xlabel='x', ylabel='y')
ax.set_title(title, y=-0.15)
ax.legend(loc='best')
ax.grid()
本章で得られる最終的な結果は下記の通りです。これは複数のカーネル関数を使用して、データを学習する前の事前分布から関数を3個サンプリングしてプロットした結果となります。この詳細を確認していきます。
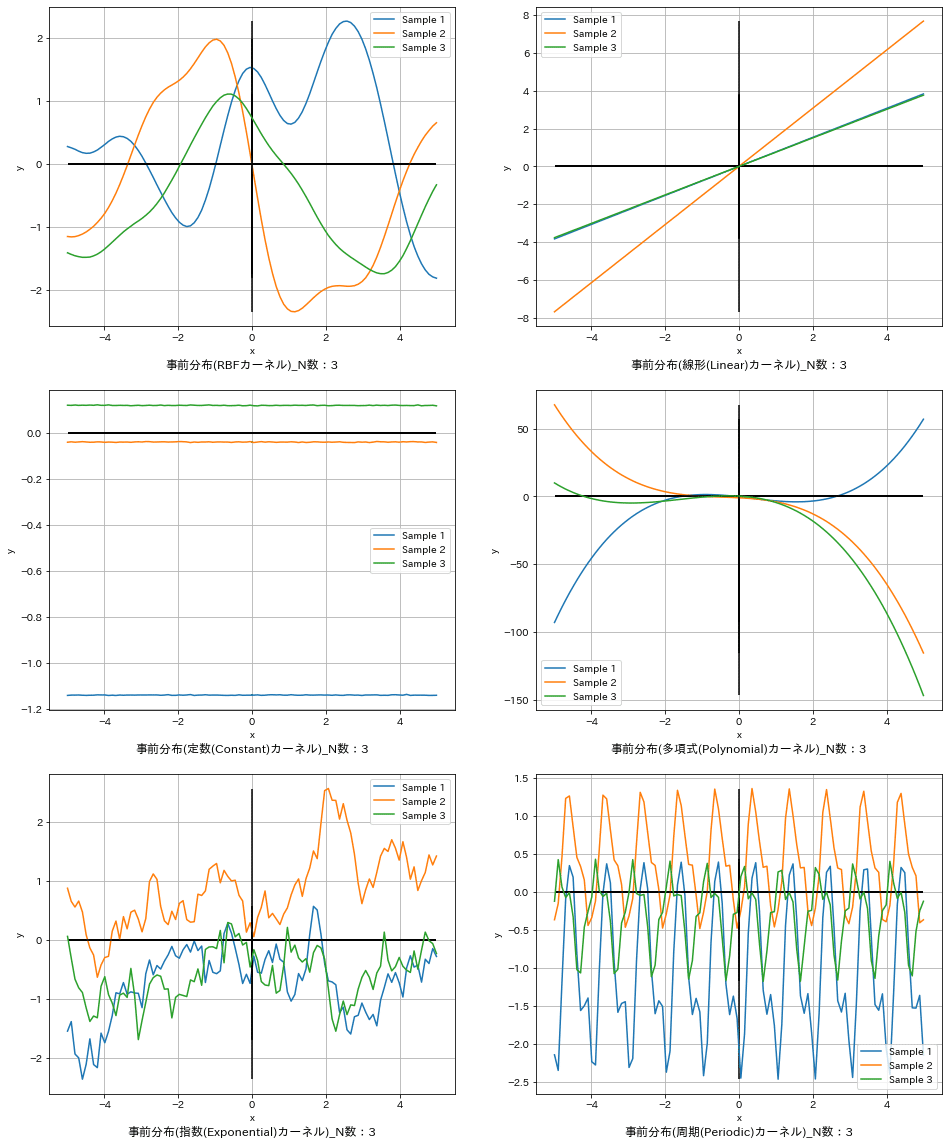
7-1.ガウス過程回帰における事前分布
まず線形回帰での事前分布を理解します。最尤推定法のように線形回帰での事前分布とは「線形回帰モデルのパラメータの分布」です。この事前分布を尤度関数(データ)を用いてベイズ更新を行い、最適化されたパラメータの分布(事後分布)を取得します。
$$
事後分布P(\theta | D)
= \frac{P(D | \theta) P(\theta)}{P(D)}
= \frac{事前分布 \times 尤度関数}{データの確率(正規化項)}
$$
$${D}$$:データ、$${\theta}$$:パラメータ(GPRでは関数)
ガウス過程回帰の事前分布は「関数$${f(x)}$$の分布」となります。この分布からサンプリングすることで入力値$${\bf x}$$に対する出力$${f(x)}$$を確率的に出力してくれます。
理解を深めるために事前分布を実装して動作検証をしました。データセットは可視化が簡単な1次元として$${N}$$個のデータ点として進めます。
$$
X=\begin{bmatrix}x_{11} \\x_{21} \\x_{31} \\ \vdots \\x_{N1} \end{bmatrix}
$$
ここから先は
¥ 500
この記事が気に入ったらチップで応援してみませんか?
