
Pythonで学ぶ統計学1:記述統計(データ・グラフ)
1.概要
本記事は統計学の学習記録用として作成しており、私が理解するのに時間がかかった場所や追って参照したい内容を中心にまとめております。
本記事のテーマは「記述統計」になります。なお資料の一部に下記(CC-BY)を使用させていただきました。
1-1.記述統計とは
統計の定義として下記がありますが、個人的に統計学は「人間の直感に頼らず、理論・確率的にデータを判断するための指標形成」だと思います。
「集団における個々の要素の分布を調べ、その集団の傾向・性質などを数量的に統一的に明らかにすること。また、その結果として得られた数値。」(例 統計をとる)(広辞苑より)
「集団現象を数量的に把握すること。一定集団について、調査すべき事項を定め、その集団の性質・ 傾向を数量的に表すこと。」(例 統計をとる)(大辞林より)
統計学は大きく分けると「記述統計」、「推測統計」、「ベイズ統計」があり今回は記述統計を説明します。
記述統計には下記の特徴があります。
【記述統計の特徴】
●取得したデータを元に解釈する(出力は確率ではなく定数):標本・母集団や分布という概念はなく、手持ちのデータ=母集団と等価の扱いとなる。
●統計量や表・グラフなどを用いてデータの特徴を表現する
●(上記より、)既存データの要約が目的となる
●一部のデータ(標本)からデータ全体(母集団)を推測できない
1-2.サンプルデータの紹介
本記事で使用したサンプルデータを紹介します。Pythonも使用しますがライブラリの詳細説明は省きますので使い方は別記事で確認お願いします
【データ1:国民健康・栄養調査14 身長・体重の平均値及び標準偏差】
記事用データとして身長と体重のデータを取得しました。下図の通りCSVは手動でダウンロードして前処理することでDataFrameとして使用できるようにしました。

[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import os
import glob
class HorizontalDisplay:
def __init__(self, *args):
self.args = args
def _repr_html_(self):
template = '<div style="float: left; padding: 10px;">{0}</div>'
return "\n".join(template.format(a._repr_html_()) for a in self.args)
# データの読み込み
filepath = 'data/FEH_00450171_230101142238.csv'
df = pd.read_csv(filepath,
encoding='shift-jis',
names=[f'{i}' for i in range(100)])
# 前処理
df = df.dropna(axis=1,thresh=10) # 欠損値が10個以上ある列を削除
df = df.dropna(axis=0,thresh=10) # 欠損値が10個以上ある行を削除
df.reset_index(drop=True,inplace=True)
df = df.fillna('') # 欠損値を空白に置換
#カラム名の設定
cols = []
for c1, c2, c3 in zip(df.loc[5], df.loc[3], df.loc[1]):
if c2 == '':
c1+=c2
else:
c1 = c1+'_'+c2
if c3 == '':
c1 += c3
else:
c1 = c1+'_'+c3
cols.append(c1)
df = df.iloc[6:, :]
df.columns = cols
#不要なインデックスを削除
def func(x):
if '総数' in x or '再掲' in x:
return False
else:
return True
df = df[df['年齢階級'].apply(func)]
#文字列型を数値型に変換するためのDict
dict_obj2float = {'人数【人】_身長(cm)_男性': int, '平均値_身長(cm)_男性': float, '標準偏差_身長(cm)_男性': float, '平均値_体重(kg)_男性': float, '標準偏差_体重(kg)_男性': float,
'人数【人】_身長(cm)_女性': int, '平均値_身長(cm)_女性': float, '標準偏差_身長(cm)_女性': float, '平均値_体重(kg)_女性': float, '標準偏差_体重(kg)_女性': float}
display(df.head())
df_2018 = df[df['時間軸(年次)']=='2018年']
df_2018 = df_2018.astype(dict_obj2float)
df_2018_main = df_2018[['時間軸(年次)', '年齢階級', '平均値_身長(cm)_男性', '平均値_身長(cm)_女性']]
mean_men, mean_women = df_2018_main['平均値_身長(cm)_男性'].mean(), df_2018_main['平均値_身長(cm)_女性'].mean()
#可視化
plt.figure(figsize=(10, 5))
plt.bar(df_2018_main['年齢階級'], df_2018_main['平均値_身長(cm)_男性'], label='男性',
align='edge', width=-0.5, color='royalblue')
plt.bar(df_2018_main['年齢階級'], df_2018_main['平均値_身長(cm)_女性'], label='女性',
align='edge', width=0.5, color='tomato')
plt.plot(df_2018_main['年齢階級'], np.ones(len(df_2018_main))*mean_men, label='男性平均',
color='blue', linestyle='--')
plt.plot(df_2018_main['年齢階級'], np.ones(len(df_2018_main))*mean_women, label='女性平均',
color = 'red', linestyle='--')
plt.xticks(rotation=90)
plt.grid()
plt.legend()
plt.show()
[OUT]

2.統計データの用語
2-1.データの種類・尺度
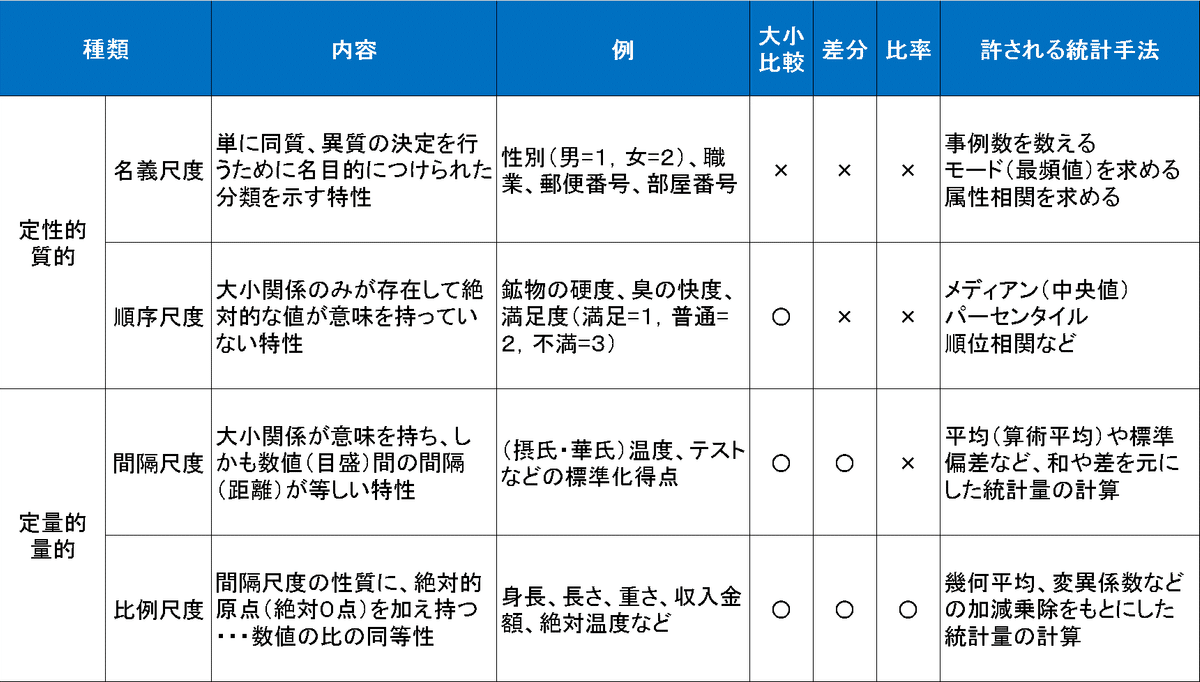
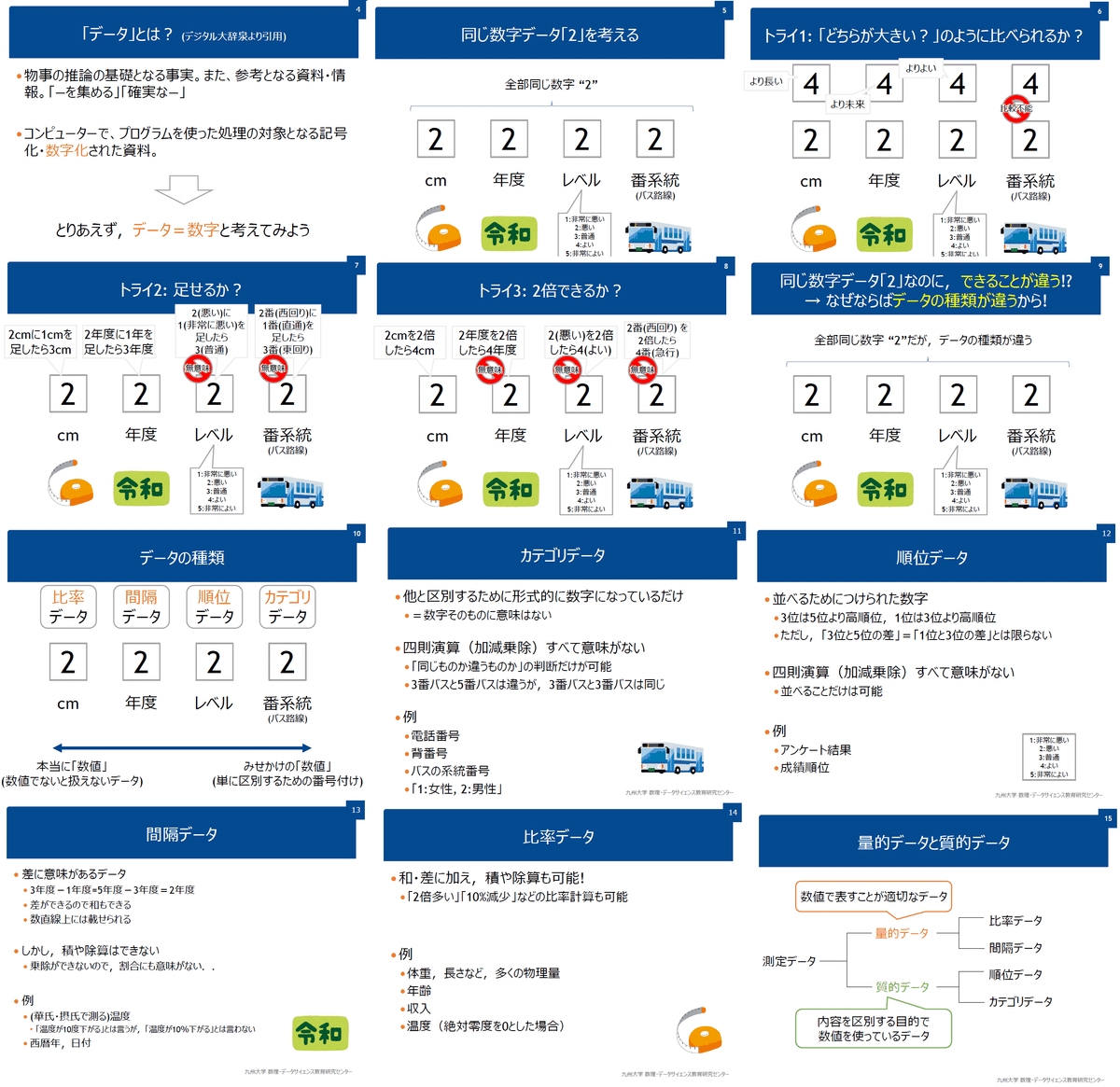
データの分類としては「量的データ」と「質的データ」の2つがあります(出典:なるほど統計学園)。
量的データ:数値(定量的)で表せるデータで数値の大小に意味がある
質的データ:データの分類や種類の区別(カテゴリカル)に使われ、順位や順序に意味があるデータ
また尺度による分け方もあり尺度は下記4種があります。名義・順序尺度が質的データ、間隔・比率尺度が量的データに対応します。
2-2.統計量
データから計算して求める指標値であり平均・分散・標準偏差などの総称
3.統計量1:代表値
代表値とはデータ全体を要約する値であり下記があります。
平均値
中央値
最頻値
四分位数
3-1.平均値
平均値は複数の種類があります。 一般的に平均値とは算術平均$${\overline{x}}$$であり、全データを合計値をデータ数Nで割ったものになります。
算術平均(相加平均 / 単純平均):データ群の重心を意味する
加重平均:特定の値(特徴量)に重心が偏るようにした平均
調和平均:逆数をとって算術平均して逆数
相乗平均:全ての積を取りn 乗根で返す
$$
\begin{aligned} 平均値\overline{x} = \frac{x_1 + x_2 + \dots + x_N}{N} = \frac{1}{N} \sum^{N}_{n=1} x_{n} \end{aligned}
$$
平均値には下記特徴があります。
データの重心に近い概念のため左右の分布が同等だと中心(中央)に寄る
外れ値に弱く、過大・過小な値に(重心が)引っ張られる傾向がある(独身男性の平均資産額が急に「500万円」も増えた理由)
データ間のばらつきを最小化する理論値のため、解釈性が高い(理解しやすい)
データ数が少ないと真値からずれる可能性が高くなる
平均値の値だけで評価するのは危険であり、ばらつきなどと合わせて比較する必要がある。
【コラム:プロ野球選手の年棒を考える】
プロ野球選手の2022年の平均年棒は4,312万円と高いため夢を追う人が多いと思いますが、平均値だけでは実情は見えません。(全データがあるか分かりませんが)「gurazeni.com」のサイトを参照して統計量を確認してみます。
結果として下記が確認できました。
前提として今回使用したデータでは平均値は約3,765万円です(4,312万円ではない)。またプロになりたいけど慣れていない人がデータに含まれていないことも理解しておく必要があります。
分散が7,284万円よりばらつきが非常に大きいことが分かります。
中央値は1,200万円, 第3四分位数(75%)でも3,600万円であり平均値以下だった。つまり平均はより上位者が押し上げていることが分かります。
ヒストグラムで確認すると大部分が左側に偏って分布している。
結論としてはプロの中でも上位側に入らないと平均年棒には達成しないため(当然ですが)プロ=稼げるというわけでもないことが分かります。
[IN※前処理]
import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import re
url = 'https://www.gurazeni.com/'
df_first = pd.read_html(url)[0]
df_master = df_first.copy()
for page in range(2, 12):
url_next = f'https://www.gurazeni.com/ranking/{page}'
df_next = pd.read_html(url_next)[0]
if len(df_next) == 0:
break
else:
df_master = pd.concat([df_master, df_next], axis=0)
df_master.reset_index(drop=True, inplace=True)
print(df_master.shape)
display(df_master)
#年俸(推定)の文字列をParseして数値に変換する関数
income_str = df_master['年俸(推定)']
def parse_income(income_str):
# 正規表現パターンによる数値抽出
pattern = r'([0-9,]+)' #0~9の数字とカンマを抽出
match = re.search(pattern, income_str) #文字列の中からパターンにマッチする最初の部分を抽出
# 正規表現にマッチしない場合は "None" を返す
if not match:
return None
# 数値文字列から数値に変換※カンマは存在しないけど念のため
income = int(match.group(1).replace(",", ""))
# 単位を取得
if "億" in income_str:
income *= 10000 * 10000
elif "万" in income_str:
income *= 10000
return income
df_income = income_str.apply(parse_income)
display(df_income)
[OUT]
(1042, 8)

[IN]
df = df_income.dropna() #欠損値(調査中(情報募集中))を削除
#カンマ区切りの数値を表示するための設定
pd.options.display.float_format = '{:,.0f}'.format
df.describe()
[OUT]
count 1,040
mean 37,648,250
std 72,838,244
min 2,200,000
25% 5,685,000
50% 12,000,000
75% 36,000,000
max 900,000,000
Name: 年俸(推定), dtype: float64[IN]
import matplotlib.pyplot as plt #正規分布を作成
import japanize_matplotlib
def conv2yen(value):
if value >= 100000000:
return f"{int(value / 100000000)}億円"
elif value >= 10000:
return f"{int(value / 10000)}万円"
else:
return f'{int(value)}円'
#ヒストグラムを作成
num_bins = 1 + np.log2(len(df)) #スタージェスの公式によるビンの数を計算
print(f'bins: {int(num_bins)}, 3.0倍: {int(3.0*num_bins)}')
counts, _bins, _ = plt.hist(df, bins=int(3.0*num_bins), color='red')
bins = _bins[:-1] + (_bins[1] - _bins[0]) / 2 #ビンの中心を計算
plt.xticks([i*0.5e8 for i in range(19)], rotation=90), plt.xlabel('年棒'), plt.ylabel('人数')
plt.gca().get_xaxis().get_major_formatter().set_scientific(False)#x軸の目盛り表示を1億単位にする
#アノテーションを追加(矢印あり)
mean, median, maxdata = conv2yen(df.mean()), conv2yen(df.median()), conv2yen(df.max())
plt.annotate(f'平均値: {mean}',
xy=(df.mean(), 100),
xytext=(df.mean(), 0.5*max(counts)),
color='blue',
arrowprops=dict(facecolor='blue', shrink=0.02))
plt.annotate(f'中央値: {median}',
xy=(df.median(), 100),
xytext=(df.median(), max(counts)),
color='green',
arrowprops=dict(facecolor='green', shrink=0.02))
plt.annotate(f'最大値: {maxdata}',
xy=(df.max(), 100),
xytext=(df.max(), 0.5*max(counts)),
color='red',
arrowprops=dict(facecolor='red', shrink=0.02))
plt.grid()
plt.show()
[OUT]
bins: 11, 3.0倍: 33
3-1-1.平均値がばらつきの理論最小値とは?
データ数$${N}$$のデータ$${x}$$と求める真値$${\mu}$$の誤差として平均二乗誤差 (MSE)を使用するとします。MSEを最小化するにはMSEの微分が0になるため下記の通りとなります。
$$
MSE=\sum_{i=1}^{N}(x_i-\mu_i)^2=\sum_{i=1}^{N}(x_i^2-2x_i\mu_i+\mu_i^2)
$$
$$
\frac{dMSE}{dx}=\frac{d}{dx}(\sum_{i=1}^{N}(x_i^2-2x_i\mu_i+\mu_i^2))=0
$$
式を変換すると
$$
\frac{d}{dx}(\sum_{i=1}^{N}x_i^2)+\frac{d}{dx}(\sum_{i=1}^{N}-2x_i\mu_i)+\frac{d}{dx}(\sum_{i=1}^{N}\mu_i^2)
$$
$$
=2\sum_{i=1}^{N}x_i-2\sum_{i=1}^{N}\mu_i+0=2\sum_{i=1}^{N}x_i-2N\mu_i=0
$$
よって下記式となりMSEの理論最小値(微分=0)が平均値と同じであることが確認できました。
$$
\mu_i=\frac{1}{N} \sum^{N}_{i=1} x_{i}
$$
3-1-2.事例で考える:工場での生産
事例として「工場内で製品重量(真値)を10gにする。製品はばらつきが発生し、得られたデータ$${x}$$が求める値になっているか確認する」を考えます。

ここでコード内では真値=10としてますが、「実際に得られるデータはサンプリングした値xのみ」であることに注意です(目標値や設定値はあっても真値(母集団の平均値)は不明)。
サンプルデータとして「真値+乱数」としてデータ数N=10で作成しました。このばらつきがあるデータの代表値(真値)の判断指標として”平均値”と”中央値”を計算しました。
結果としてサンプリングした値の平均値は真値に近い値となり、代表値として適切であることが確認できます。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.set_printoptions(precision=3, suppress=True) #小数点以下3桁表示、指数表示しない
np.random.seed(123)#乱数の種を設定
nums_sample = 10 #サンプル数
target_value = 10 #真値(目標値)とする値
x = target_value + np.random.randn(nums_sample) #真値にばらつきを追加
# print(np.sort(x))
x_real = np.full_like(x, target_value) #真値を格納した配列
x_mean = np.full_like(x, x.mean()) #平均値を格納した配列
x_median = np.full_like(x, np.median(x)) #中央値を格納した配列
#可視化
plt.figure(figsize=(10, 6), facecolor='w')
plt.scatter(range(nums_sample), x, label='Data', color='blue', marker='o') #サンプルデータ
plt.plot(x_real, label='Target', color='red', linestyle='dashed') #真値
plt.plot(x_mean, label='Mean', color='green', linestyle='dashed') #平均値
plt.plot(x_median, label='Median', color='orange', linestyle='dashed') #中央値
plt.grid(), plt.legend(), plt.xlabel('サンプルデータ数'), plt.ylabel('計測値')
plt.show()
[OUT]
[ 7.573 8.494 8.914 9.133 9.421 9.571 10.283 10.997 11.266 11.651]
参考として「大数の法則」より試行回数(nums_sample)Nを大きくすると取得したデータの平均値(標本平均)は母平均(真値)に近づきます。

3-2.中央値
中央値とはサンプル数Nのデータにおいて、昇順(小->大)に並べたときに$${\frac{N}{2}}$$番目(中央)に位置するデータです。
Numpyではnp.median(), Pandasではdf.median()で計算できます。
[IN]
print(np.median(x), pd.DataFrame(x).median())
plt.figure(figsize=(10, 6), facecolor='w')
plt.bar(np.arange(nums_sample), np.sort(x)) #サンプルデータ
plt.xticks(np.arange(nums_sample), np.arange(nums_sample)), plt.xlabel('サンプル数') #x軸の目盛り
plt.text(4.5, 10.5, '中央値', color='red') #テキスト追加
plt.arrow(5, 10.3, 0, -0.5, color='red', head_width=0.2, head_length=0.1) #矢印追加
plt.show()
[OUT]
9.4962435 9.496244
中央値には下記のような特徴があります。
データのソートが必須のため計算負荷は平均値より大きい。
外れ値に強く過大・過小な値に(重心が)引っ張られない(出典:中心的な傾向を捉える)。
特定の条件では平均値より確からしい結果となる(出典:日本の給与水準は「変わってない」? 年収中央値の推移は?)

3-3.四分位数
下記をまとめての総称を四分位数(quartile points)と言います。
第1四分位数:データをソートした時の25%の位置
第2四分位数(中央値):データをソートした時の50%の位置
第3四分位数:データをソートした時の75%の位置

Numpyではnp.quantile()やnp.percentile(), Pandasではdf.quantile()で計算できます。
[IN]
a_1, a_2, a_3 = np.quantile(x, 0.25), np.quantile(x, 0.5), np.quantile(x, 0.75) #第1四分位数、第2四分位数、第3四分位数
print(f'第1四分位数:{a_1:.3f}, 第2四分位数:{a_2:.3f}, 第3四分位数:{a_3:.3f}')
a_1p, a_2p, a_3p = np.percentile(x, 25), np.percentile(x, 50), np.percentile(x, 75) #第1四分位数、第2四分位数、第3四分位数
print(f'第1四分位数:{a_1p:.3f}, 第2四分位数:{a_2p:.3f}, 第3四分位数:{a_3p:.3f}')
df = pd.DataFrame(x, columns=['Data'])
a_1df, a_2df, a_3df = df.quantile(0.25), df.quantile(0.5), df.quantile(0.75) #第1四分位数、第2四分位数、第3四分位数
print(f'第1四分位数:{a_1df[0]:.3f}, 第2四分位数:{a_2df[0]:.3f}, 第3四分位数:{a_3df[0]:.3f}')
[OUT] ※3つとも同じ出力
第1四分位数:8.969, 第2四分位数:9.496, 第3四分位数:10.8193-4.最頻値
最頻値とはデータの中で最も出現する頻度が多い数です。量的データではなく質的データで使用します(最も売れている服のサイズなど)。
Numpy、Pandasともに最頻値の計算は一工夫が必要です。
[IN]
#データ作成
clothes_sizes = np.random.choice(['S','M','L','XL'], 20)
print(clothes_sizes)
#Numpy
uniqs, count = np.unique(clothes_sizes, return_counts=True) #要素の種類を取得
idx = np.argmax(count)
print(f'最頻値:{uniqs[idx]}, 数:{count[idx]}')
#Pandas
df_clothes = pd.Series(clothes_sizes)
df_clothes.mode()[0], df_clothes.value_counts()['L']
[OUT]
['L' 'M' 'L' 'L' 'S' 'L' 'L' 'M' 'XL' 'L' 'XL' 'M' 'L' 'M' 'S' 'M' 'L'
'XL' 'M' 'S']
最頻値:L, 数:8
('L', 8)3-5.代表値を考える:年収の推移
日本の給与推移額として「平均給与額」が使用されておりますが、”ばらつき”が考慮されておりません。よって(抽出したデータ内の)日本全体の平均は分かりますが貧富の差などはわかりません(参考として貧富差の指標として「ジニ係数」があります)。
なお、年収に関しては平均値ではなく中央値の方が感覚に近くなります。参考として「厚生労働省 2021年 国民生活基礎調査の概況-各種世帯の所得等の状況」より、平均値と中央値の差を確認しました。結果として、多くの方が平均値より中央値の方が実感に近い値になったと思います。


4.統計量2:散布度(ばらつき)
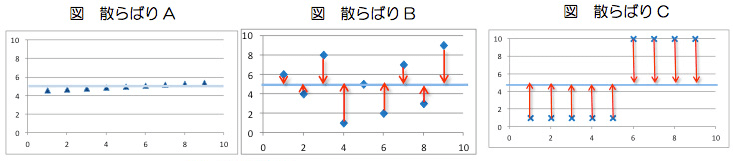
データ集団は代表値だけではデータ全体の様子をとらえる事ができません。データを捉えるためには中心的な傾向だけではなく、データの散らばり具合にも着目しなければなりません(出典:データの散らばりを捉える)。
4-1.範囲(Range):最大値/最小値
データ群で最も大きい値を最大値(MAX)、小さい値を最小値(MIN)と呼びます。Numpy、Pandasともにmax(), min()メソッドで取得可能です。
また分布の最大値と最小値の差を範囲と呼びます。
$$
範囲(Range)=最大値-最小値
$$
4-2.分散と標準偏差σ
ばらつきはデータの散らばり度合を表す指標です。平均値を$${\bar{x} }$$、データ数nとする時、ばらつきの指標は分散と標準偏差があります。
また分散には標本分散と不偏分散があります。詳細は別記事で説明する予定ですが概要は下記の通りです。
分散$${\sigma^2}$$:平均値$${\bar{x}}$$との誤差$${(x_i - \bar{x})}$$の2乗和の平均(2乗にすることで誤差が負の値でも問題ない)
標準偏差$${\sigma}$$:分散の平方根であり、元データと同じ単位で扱うことができデータ解析のばらつきは$${\sigma}$$を使用する。データが正規分布に従う場合は±kσ間に存在するデータの確率は理論的に求まる。
標本分散と不偏分散:記述統計では使用しませんが、推測統計では不変分散が出てきます。理由として、母集団に比べ標本数が少ない時は標本分散が母分散よりも小さくため、標本分散が母分散に等しくなるように補正した分散が必要なためです。
$$
(標本)分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})^2
$$
$$
標準偏差\sigma = \sqrt{\sigma^2}
$$
$$
不偏分散\sigma^2= \frac{1}{n-1}\sum_{i=1}^{n} (x_i – \bar{x})^2
$$
【コラム1:標準偏差と品質管理】
「確率密度:正規分布」で紹介しますが、データの発生確率の分布は標準偏差$${\sigma}$$に関係があり、$${±k\sigma}$$内で発生する確率は数式で計算が可能です。例として正規分布では$${±1.96 \sigma}$$内で95%の発生確率となります。
シックスシグマと呼ばれる品質管理手法は製品の品質を$${±6\sigma}$$内に抑えることで不良品発生率を100万回に3~4回に抑えることです。
重要なこととしてはシックスシグマを適用するには検査基準値があり、その基準値に製品が収まるようにばらつきを小さくすることです。そのためにはばらつきの原因を把握してそれを対策する必要があります。
(あくまで検査基準値を緩めるという意味ではありません)

【コラム2:分散に関する補足】


4-3.Python実装時の注意点
デフォルトとして「Numpy:標本分散、Pandas:不偏分散」の値が出力されます。Numpyで不偏分散を計算する場合は引数"ddof=1"とします。
自分が求める手法にあった統計値を選定する必要があります。
[IN]
x = np.random.randn(100)
mean, var, std = x.mean(), x.var(), x.std()
print(f'Numpy 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
mean, var, std = x.mean(), x.var(ddof=1), x.std(ddof=1)
print(f'Numpy 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
df_x = pd.DataFrame(x, columns=['x'])
mean, var, std = df_x['x'].mean(), df_x['x'].var(), df_x['x'].std()
print(f'Pandas 平均:{mean:.3f}, 分散: {var:.3f}, 標準偏差: {std:.3f}')
[OUT]
Numpy 平均:0.027, 分散: 1.273, 標準偏差: 1.128
Numpy 平均:0.027, 分散: 1.286, 標準偏差: 1.134
Pandas 平均:0.027, 分散: 1.286, 標準偏差: 1.1345.標準化
5-1.標準化
標準化とは「平均値0、標準偏差1」にデータを加工することあり、数式は下記の通りです。標準化の特徴は下記の通りです。
データスケールを統一できるため異なるデータとの比較がしやすい
正規分布へ適用できる(下図参照)
$$
標準化=\frac{x - \overline{x}}{\sigma}
$$
データ:$${x}$$、平均値:$${\overline{x}}$$、標準偏差:$${\sigma}$$

5-2.標準得点(Z得点)/偏差値
標準得点とは平均値や標準偏差などの集団基準を用い、母集団の中における個人の相対的な位置づけがわかるように変換した得点のことであり、下記式で表すことができます。
S=1, M=0はz得点と呼ばれ標準化と同じであり、S=10, M=50はZ得点と呼ばれ日本の受験で使用される偏差値と同じとなります。偏差値70というと上図より上位2.3%であることがわかります。
$$
標準得点=\frac{x - \overline{x}}{\sigma}\times S+M
$$
$$
偏差値=\frac{x - \overline{x}}{\sigma}\times 10+ 50
$$
データ:$${x}$$、平均値:$${\overline{x}}$$、標準偏差:$${\sigma}$$、標準得点の標準偏差:S、標準得点の平均値:M
5-3.Pythonでの計算(標準化):StandardScaler()
PandasやNumpyで標準化するメソッドはないため関数を自作するかscikit-learnの”StandardScaler()”を使用します。
6.相関
2つのデータ間の関係を表す指標としては共分散と相関係数があります。共分散はデータのスケールで値が変わるため通常は相関係数を使用します。
共分散:2変数($${x}$$, $${y}$$)の関係の強さを表す指標の一つであり「$${X}$$の偏差 × $${Y}$$の偏差の平均」となる。注意点としてスケール変換に対して不変でなくデータの単位の影響を受けるので値の大きさで単純に比較できない。
相関係数:2 変量データの間にある相関関係(= 線形な関係)の強弱を示す指標であり‐1.0から1.0の範囲で表される。
6-1.因果関係と相関関係の違い
基礎的なことですが、因果関係と相関関係はまったく別物です。因果関係は「要因が結果に影響する直接的な原因であること」ですが相関関係は「2つの事象・結果が同じ線上にある(相関係数が1や-1に近い)」だけです。
よって、相関関係があっても必ずしも因果関係あるわけではありません。疑似相関の可能性もあるため事象の背景は解析者が考える必要があります。
(出典:おもしろ統計・120疑似相関って知っていますか?)。

面白い事例として下記動画が参考になります。
6-2.共分散:Cov(X, Y)
共分散(Covariance)は下記の通りであり「X の偏差 × Y の偏差」の平均」を意味します。特徴は下記の通りです。
共分散が大きい(正)→ $${X}$$ が大きいとき Y$${Y}$$も大きい(同じ方向に動く)
共分散が 0に近い→ $${X}$$ と $${Y}$$ にあまり関係はない(独立である)
共分散が小さい(負)→ $${X}$$ が大きいとき $${Y}$$は小さい(違う方向に動く)
共分散の意味として”多次元での分散”に近く、2次元の正規分布における分散(の一部)に使用される
$${X}$$=$${Y}$$の場合は1次元の分散と同じ形になる->共分散は分散の一般化
数値($${X}$$や$${Y}$$)の大小で共分散の数値の大きさが変わるため、$${Cov()}$$の数値比較には意味がない(※1次元でも身長と体重の分散の比較は意味がないのと同じ意味)。
よって$${Cov()}$$の大小だけでどの程度の相関があるかは判断できない。
$$
共分散{{\rm Cov}(X,Y)} = \frac{1}{n}\sum_{i=1}^{n}(x_i -\bar{x})(y_i - \bar{y})
$$
$$
Xの分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - \bar{x})(x_i - \bar{x})
$$
$$
Yの分散\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} (y_i - \bar{y})(y_i - \bar{y})
$$
6-3.相関係数:Corr(X, Y)
相関係数の詳細を説明します。なお参考資料は下記の通りです。

6-3ー1.特徴および数式
前述の通り共分散$${Cov(X,Y)}$$の絶対値では他の$${Cov()}$$との比較はできず、値から相関関係の程度を把握できないため正規化する必要があります。$${Cov(X,Y)}$$を-1~1に正規化した値が相関係数となります。
相関係数$${{\rm Corr}(X, Y)}$$は数式より下記特徴があります。
【相関係数rの傾向や特徴】
相関係数は共分散Cov(X,Y)を各変数X, Yの標準偏差σで割った値である
標準化(平均0, 分散1)されているため他の相関係数とも比較が可能
各変数のスケールを変更しても標準化されるため、片方を定数倍しても相関係数の値は変わらない(データの大小に依存しない)
相関係数の性質として下記がある。
性質1:値は-1~1であり変数X,Yのスケールによらず比較できる
性質2:Corr(X,Y)の値の大小でXとYの関係性が判断できる
性質3:Corr(X,Y)=1のときXとYの値は全て同一線上となる
相関係数rは基本的に線形の関係度(強さ)を示す。よってsignカーブなど関係があっても線形関係に無いものはrが小さくなる(※無相関だとしても無関係とは限らないことを意味します。)
相関係数rの数値の大きさで線形関係が強いかを示す
傾きには依存せず、ばらつき度合いが同じであれば同じrとなる。

【数式】
$$
{\rm Corr}(X, Y)
=\frac{共分散}{\sqrt{xの分散 \times yの分散}}
=\frac{{\rm Cov}(X, Y)}{\sqrt{{\rm Var}(X){\rm Var}(Y)}}
=\frac{{\rm Cov}(X, Y)}{\sigma_x \sigma_y}
$$
$$
=\frac{\frac{1}{n}\sum_{i = 1}^n (x_i - \bar{x})(y_i - \bar{y})} {\sqrt{\frac{1}{n}\sum_{i = 1}^n (x_i - \bar{x})^2}\sqrt{\frac{1}{n}\sum_{i = 1}^n (y_i - \bar{y})^2}}= \frac{\frac{1}{n}\sum_{i = 1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sigma_x \sigma_y}
$$
$$
=\frac{1}{n}\sum_{i=1}^n \frac{x_i - \bar{x}}{\sigma_x} \cdot \frac{y_i - \bar{y}}{\sigma_y}
=\frac{1}{n}\sum_{i=1}^n(標準化x)(標準化y)
$$
6-3ー2.参考1:XとYが同一線上時を確認
$$
\bar{y} = \frac{1}{n} \sum^{n}_{n=1} y_{n}
=\frac{1}{n} \sum^{n}_{n=1} (ax_{n}+b)
=a\bar{x} + b
$$
$$
\sigma_y^2 = \frac{1}{n}\sum_{i=1}^{n} (y_i - \bar{y})^2=\frac{1}{n}\sum_{i=1}^{n} ((ax_i+b) - (a\bar{x} + b))^2=\frac{1}{n}\sum_{i=1}^{n} (a(x_i-\bar{x}))^2
$$
$$
\sigma_y=a\sigma_x
$$
$$
{\rm Corr}(X, Y)
=\frac{1}{n}\sum_{i=1}^n \frac{x_i - \bar{x}}{\sigma_x} \cdot \frac{y_i - \bar{y}}{\sigma_y}
=\frac{1}{n}\sum_{i=1}^n \frac{x_i - \bar{x}}{\sigma_x} \cdot \frac{a(x_i-\bar{x})}{a\sigma_x}
$$
$$
=\frac{1}{n}\sum_{i=1}^n \frac{(x_i - \bar{x})^2}{\sigma_x^2}=\frac{1}{\sigma_x^2}\times \sigma_x^2=1
$$
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
def linear(x, a, b):
return a * x + b
def getminmax(x):
min, max = x.min(), x.max()
if np.abs(min) > np.abs(max):
return np.abs(min)
else:
return np.abs(max)
# データの作成
np.random.seed(1233)
x = np.random.randn(20) * 10
y = linear(x, 2, 3)
#x軸とy軸の最大値を取得(軸設定)
xtick = getminmax(x)
ytick = getminmax(y)
#グラフの描画
fig, axs = plt.subplots(3, 2, figsize=(14, 18), facecolor='w', edgecolor='k')
axs[0][0].scatter(x, y, s=50, c='r', marker='o', label='data')
#x軸とy軸を記載
axs[0][0].plot([-xtick, xtick], [0,0], c='black', lw=1)
axs[0][0].plot([0,0], [-ytick, ytick], c='black', lw=1)
axs[0][0].set(title='y=ax+b(オリジナル)',
xlabel='x',
ylabel='y')
axs[0][0].grid()
#x軸を標準化
x_mean, y_std = x.mean(), x.std()
x_std = (x - x_mean) / y_std #標準化
axs[0][1].scatter(x_std, y, s=50, c='r', marker='o', label='data')
axs[0][1].plot([-xtick, xtick], [0,0], c='black', lw=1)
axs[0][1].plot([0,0], [-ytick, ytick], c='black', lw=1)
axs[0][1].set(title='y=ax+b(x軸を標準化)',
xlabel='x(標準化)',
ylabel='y')
axs[0][1].grid()
axs[0][1].annotate('xの平均0, 分散1へ圧縮', xy=(5, -10), xytext=(15, -10),
arrowprops=dict(facecolor='red', shrink=0.05))
axs[0][1].annotate('', xy=(-5, 10), xytext=(-15, 10),
arrowprops=dict(facecolor='red', shrink=0.05))
#y軸を標準化
y_mean, y_std = y.mean(), y.std()
y_std = (y - y_mean) / y_std #標準化
axs[1][0].scatter(x, y_std, s=50, c='r', marker='o', label='data')
axs[1][0].plot([-xtick, xtick], [0,0], c='black', lw=1)
axs[1][0].plot([0,0], [-ytick, ytick], c='black', lw=1)
axs[1][0].set(title='y=ax+b(y軸を標準化)',
xlabel='x',
ylabel='y(標準化)')
axs[1][0].grid()
axs[1][0].annotate('yの平均0, 分散1へ圧縮', xy=(5, -10), xytext=(5, -30),
arrowprops=dict(facecolor='red', shrink=0.05))
axs[1][0].annotate('yの平均0, 分散1へ圧縮', xy=(-5, 10),xytext=(-5, 30),
arrowprops=dict(facecolor='red', shrink=0.05))
#y軸も標準化
y_mean, y_std = y.mean(), y.std()
y_std = (y - y_mean) / y_std #標準化
axs[1][1].scatter(x_std, y_std, s=50, c='r', marker='o', label='data')
axs[1][1].plot([-xtick, xtick], [0,0], c='black', lw=1)
axs[1][1].plot([0,0], [-ytick, ytick], c='black', lw=1)
axs[1][1].set(title='y=ax+b(x・y軸を標準化)',
xlabel='x(標準化)',
ylabel='y(標準化)')
axs[1][1].grid()
axs[1][1].annotate('xの平均0, 分散1へ圧縮', xy=(5, -10), xytext=(15, -10),
arrowprops=dict(facecolor='red', shrink=0.05))
axs[1][1].annotate('', xy=(-5, 10), xytext=(-15, 10),
arrowprops=dict(facecolor='red', shrink=0.05))
axs[1][1].annotate('yの平均0, 分散1へ圧縮', xy=(5, -10), xytext=(5, -30),
arrowprops=dict(facecolor='red', shrink=0.05))
axs[1][1].annotate('yの平均0, 分散1へ圧縮', xy=(-5, 10),xytext=(-5, 30),
arrowprops=dict(facecolor='red', shrink=0.05))
#x軸とy軸を標準化(拡大)
xtick_std, ytick_std = getminmax(x_std), getminmax(y_std)
axs[2][0].scatter(x_std, y_std, s=50, c='r', marker='o', label='data')
axs[2][0].plot([-xtick_std, xtick_std], [0,0], c='black', lw=1)
axs[2][0].plot([0,0], [-ytick_std, ytick_std], c='black', lw=1)
axs[2][0].set(title='y=ax+b(x・y軸を標準化(拡大))',
xlabel='x(標準化)',
ylabel='y(標準化)')
axs[2][0].grid()
axs[2][0].text(0.5, 1.5, 'xyは正(x:+, y:+)', fontsize=14, color='red')
axs[2][0].text(-1.5, -1.5, 'xyは正(x:-, y:-)', fontsize=14, color='red')
axs[2][0].text(0.5, -1.5, 'xyは負(x:+, y:-)', fontsize=14, color='blue')
axs[2][0].text(-1.5, 1.5, 'xyは負(x:-, y:+)', fontsize=14, color='blue')
#標準化したxとyの積を計算
xy_std = x_std * y_std
xytick = getminmax(xy_std)
print(f'xyのデータ数:{len(xy_std)}')
print(f'相関係数:{xy_std.sum()/len(xy_std)}') #相関係数=Cov(x,y)/σxσy=(1/n)Σ(x-μx)(y-μy)/σxσy=(1/n)Σ(標準化x)(標準化y)
axs[2][1].scatter(xy_std, np.zeros_like(xy_std), s=30, c='r', marker='x', label='data')
axs[2][1].plot([0, xytick], [0,0], c='black', lw=1)
axs[2][1].set(title='標準化x×標準化y',
xlabel='x(標準化)×y(標準化)の1次元プロット')
axs[2][1].grid()
#y軸を非表示
axs[2][1].axes.yaxis.set_visible(False)
plt.show()
[OUT]
xyのデータ数:20
相関係数:1.0000000000000004
6-3ー3.参考2:sin(x)の相関係数を確認
参考としてsin(x)の相関係数も計算・図示してみました。
[IN]
def classify_xy(x, y):
if x>=0 and y>=0:
return 0
elif x<0 and y<0:
return 1
elif x>=0 and y<0:
return 2
elif x<0 and y>=0:
return 3
else:
None
x = np.linspace(-2*np.pi, 2*np.pi, 21)
y = np.sin(x)
fig, axs = plt.subplots(2, 2, figsize=(12, 12), facecolor='w', edgecolor='k')
#Fig.1 y=sin(x)
axs[0][0].scatter(x, y, s=30, c='r', marker='o', label='data')
axs[0][0].plot(x, y, c='b', lw=0.2, ls='--') #確認用
axs[0][0].plot([-2*np.pi, 2*np.pi], [0,0], c='black', lw=1)
axs[0][0].plot([0,0], [-1,1], c='black', lw=1)
axs[0][0].set(title='y=sin(x)', xlabel='x', ylabel='sin(x)')
axs[0][0].grid()
#Fig.2 y=sin(x)をx軸・y軸ともに標準化
mean_x, std_x, mean_y, std_y = x.mean(), x.std(), y.mean(), y.std()
x_std, y_std = (x - mean_x) / std_x, (y - mean_y) / std_y
axs[0][1].scatter(x_std, y_std, s=30, c='r', marker='o', label='data')
axs[0][1].plot([-2*np.pi, 2*np.pi], [0,0], c='black', lw=1)
axs[0][1].plot([0,0], [-1,1], c='black', lw=1)
axs[0][1].set(title='y=sin(x)のx・yを標準化', xlabel='x(標準化)', ylabel='sin(x)(標準化)')
axs[0][1].grid()
axs[0][1].text(2.0, 1.0, 'xyは正(x:+, y:+)', fontsize=14, color='red')
axs[0][1].text(-6.0, -1.0, 'xyは正(x:-, y:-)', fontsize=14, color='red')
axs[0][1].text(2.0, -1.0, 'xyは負(x:+, y:-)', fontsize=14, color='blue')
axs[0][1].text(-6.0, 1.0, 'xyは負(x:-, y:+)', fontsize=14, color='blue')
#Fig.3 色分けしたプロットを作成
classes = np.vectorize(classify_xy)(x_std, y_std)
df = pd.DataFrame({'x':x, 'y':y, 'x_std':x_std, 'y_std':y_std, 'class':classes})
df0, df1, df2, df3 = df[df['class']==0], df[df['class']==1], df[df['class']==2], df[df['class']==3]
axs[1][0].scatter(df0['x_std'], df0['y_std'], s=30, c='r', marker='o', label='label0:x:+, y:+')
axs[1][0].scatter(df1['x_std'], df1['y_std'], s=30, c='b', marker='^', label='label1:x:-, y:-')
axs[1][0].scatter(df2['x_std'], df2['y_std'], s=30, c='g', marker='s', label='label2:x:+, y:-')
axs[1][0].scatter(df3['x_std'], df3['y_std'], s=30, c='y', marker='x', label='label3:x:-, y:+')
axs[1][0].plot([-2*np.pi, 2*np.pi], [0,0], c='black', lw=1)
axs[1][0].plot([0,0], [-1,1], c='black', lw=1)
axs[1][0].set(title='y=sin(x)のx・yを標準化(色分けVer.)', xlabel='x(標準化)', ylabel='sin(x)(標準化)')
axs[1][0].grid(), axs[1][0].legend()
#Fig.4 y=sin(x)をx軸・y軸ともに標準化したxとyの積を計算
df['xy'] = df['x_std'] * df['y_std']
df0, df1, df2, df3 = df[df['class']==0], df[df['class']==1], df[df['class']==2], df[df['class']==3]
axs[1][1].scatter(df0['xy'], df0['xy']*0, s=20, c='r', marker='o', label='label0:x:+, y:+')
axs[1][1].scatter(df1['xy'], df1['xy']*0, s=20, c='b', marker='^', label='label1:x:-, y:-')
axs[1][1].scatter(df2['xy'], df2['xy']*0, s=20, c='g', marker='s', label='label2:x:+, y:-')
axs[1][1].scatter(df3['xy'], df3['xy']*0, s=20, c='y', marker='x', label='label3:x:-, y:+')
axs[1][1].plot([-2, 2], [0,0], c='black', lw=1)
axs[1][1].set(title='y=sin(x)のx・yを標準化したxとyの積を計算', xlabel='x(標準化)×sin(x)(標準化)の1次元プロット')
axs[1][1].axes.yaxis.set_visible(False)
axs[1][1].grid(), axs[1][1].legend()
plt.show()
print(f'xyのデータ数:{len(xy)}')
print(f'相関係数:{df["xy"].sum()/len(df["xy"])}') #相関係数=Cov(x,y)/σxσy=(1/n)Σ(x-μx)(y-μy)/σxσy=(1/n)Σ(標準化x)(標準化y)
[OUT]
xyのデータ数:21
相関係数:-0.3507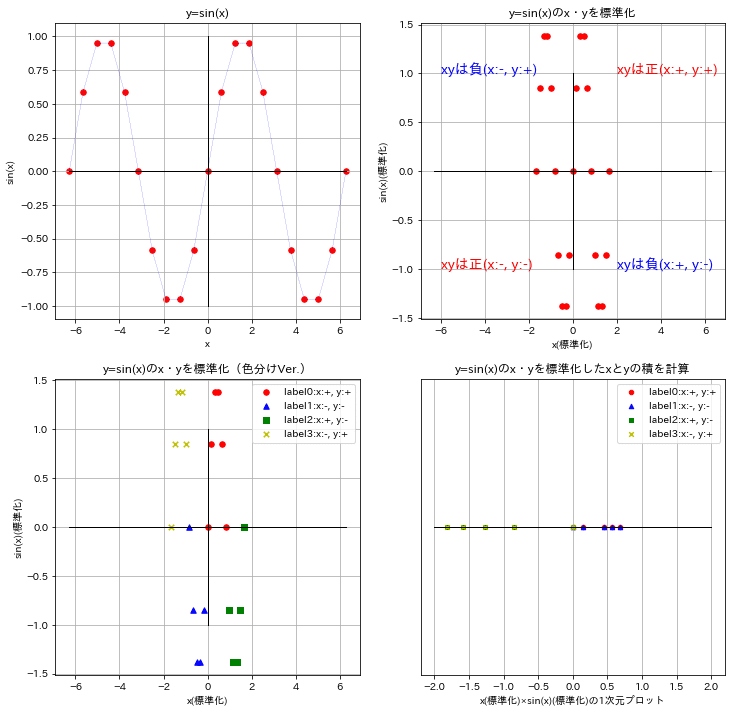
6-4.Pythonでの計算(相関係数):corr()
相関係数はPandas:corr()メソッド、Numpy:corrcoef()で計算できます。1-2節で紹介した「2018年の年齢別男女の身長」に相関があるか確認します。
結果として相関係数は高く相関(男女で年齢ごとの身長の伸び方は相関がある)が確認されました。
[IN]
df_2018_men, df_2018_women = df_2018_main[['年齢階級', '平均値_身長(cm)_男性']], df_2018_main[['年齢階級', '平均値_身長(cm)_女性']]
display(HorizontalDisplay(df_2018_men.T, df_2018_women.T))
df_2018_main.corr()
[OUT]
平均値_身長(cm)_男性 平均値_身長(cm)_女性
平均値_身長(cm)_男性 1.000000 0.988219
平均値_身長(cm)_女性 0.988219 1.000000
7.グラフ:全般
7-1.グラフの種類
表(テーブルデータ)だけではデータを直感的に理解が難しいためデータの可視化が重要であり、そのための手段としてグラフがあります。グラフには下記のようなものがあります。
(余談ですが、今の会社の中には表だけで結論を言う人が多いですが、個人的にはそういう人たちが何を言いたいかは理解できないことが多いです)



7-2.グラフの特徴
グラフ化の目的としては下記があり、目的に応じたグラフの選定が必要です。またグラフ化前後でデータそのものの深堀・検証(サンプル数は十分か、変なばらつきが発生していないか)は必要です。
データ同士の比較
データの分布・偏り
データ同士の(相関)関係

7-3.参考1:錯視(詐欺)グラフ
グラフはうまく使う?と真実とは異なるような見せ方をすることも可能です。下記に錯視を使ったグラフの例を紹介します。

7-4.参考2:Pythonの可視化ライブラリ
各種グラフは下記ライブラリよりPythonで作成可能です。
8.グラフ:詳細
8-1.ヒストグラム(度数分布図)
ヒストグラムとは「身長のような連続値データの出現頻度を分布として表現する手法」です。
まず初めに、サイコロのような離散値ではデータの区切りが明確なためデータ数(度数)は簡単にカウントできるため下図のように分布を作成できます。(度数÷試行数=確率から確率質量分布が作れますが、この詳細は「Pythonで学ぶ統計学3:確率変数と確率分布」で紹介しています。)

次に身長のような連続値のデータを考えます。連続値ではデータに区切りがないためそのままでは数値をカウントできず分布を作成できません(ほとんどの数値が度数1となる)。
$$
\begin{bmatrix} 167 & 172 & 188 & 154 & 180 & 195 & 160 & 177 & 185 & 169 & 192 & 157 & 174 & 181 & 159 & 186 & 175 & 190 & 166 & 198 \end{bmatrix}
$$
そこでデータをいくつかの階級(データを一定の範囲で区切ったもの)に分けることで連続値でも階級内において度数をカウントすることができるようになります。得られた階級と度数の表を度数分布表と言います。
この度数分布表のデータから、横軸に階級、縦軸に度数(その階級に含まれるデータの数)をプロットして得られた分布がヒストグラムとなります。ヒストグラムの特徴は下記の通りです。
横軸の階級は「自分で自由に設定が可能」であり「階級によりグラフの高さ(度数)」が変わることに注意が必要です。
相対度数(度数÷全データ)の合計(つまりビンの高さの合計)は1になるが面積の合計は1にはならない。つまりヒストグラムは確立モデルではないため、確率密度分布と同じに扱うことはできません。
階級の範囲は全て同じではなく異なる幅で設定可能なため、面積そのものはデータ割合の意味を示します。
度数を全データ数で割った相対度数をプロットすることで確率密度分布の近似分布は作成できるが同じものではないため、あくまでデータ分布の可視化ツールとしての用途で使用する。
【身長のヒストグラム】
連続値の身長のデータからヒストグラムを作成してみます。下記の通り、連続値を一定の範囲で階級分けすることで度数としてカウント可能な状態となりデータの分布を確認することが出来ました。
[IN]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
heights = np.array([167, 172, 188, 154, 180, 195, 160, 177, 185, 169, 192, 157, 174, 181, 159, 186, 175, 190, 166, 198])
print(f'MIN:{heights.min()}, MAX:{heights.max()}')
hist, bins = np.histogram(heights, bins=5)
print(f'度数:{hist}, bins(階級):{bins}')
relative_frequecy = hist/len(heights)
print(f'相対度数:{relative_frequecy}, 相対度数の合計:{relative_frequecy.sum()}')
cumulative_frequency = np.cumsum(relative_frequecy)
print(f'累積度数:{cumulative_frequency}')
bin_width = bins[1] - bins[0]
plt.bar(bins[:-1], hist, width=bin_width, align='edge', edgecolor='white')
for i, h in enumerate(hist):
plt.text(bins[i]+bin_width/2, h, str(h), ha='center', va='bottom', fontsize=14)
#累積度数(Cumulative Frequency)
plt.plot(bins[:-1]+bin_width/2, cumulative_frequency, marker='o', color='white')
for i, c in enumerate(cumulative_frequency):
plt.text(bins[i]+bin_width/2, c, str(c), ha='center', va='bottom', fontsize=12, color='white')
[OUT]
MIN:154, MAX:198
度数:[4 3 5 4 4], bins(階級):[154. 162.8 171.6 180.4 189.2 198. ]
相対度数:[0.2 0.15 0.25 0.2 0.2 ], 相対度数の合計:1.0
累積度数:[0.2 0.35 0.6 0.8 1. ]
8-1-1.度数分布表
度数分布表(frequency distribution)とは下記内容を表にしたものです。
度数(Frequency):特定のビン(階級)に含まれるデータの数を示します。ヒストグラムでは、各ビンの高さが度数を表すため、データがどの程度集中しているかを視覚的に把握できます。
階級(bin):連続データを一定の範囲に区切ったものです。ビンの幅や数は、データの特性や目的に応じて選択されます。
階級値(class value):その階級を代表する値であり、通常は階級の中央値をとる(階級値の設定は分析者が自由に設定可能である。)
相対度数(relative frequency):各ビンの度数を全データ数で割ったもので、そのビンに含まれるデータの割合を示します。相対度数を使用することで、ヒストグラムを確率的な視点から解釈することができます。
累積相対度数:特定の階級までの相対度数の累積和であり、ある値以下のデータがどれだけ含まれているかを把握できます。
$$
ある階級の相対度数=\frac{ある階級の度数}{全度数の合計}
$$

8-1-2.Pythonでの実装:numpy.histogram
Numpyでの実装は”numpy.histogram”を使用します。
[numpy.histogram()のAPI確認]
numpy.histogram(a, bins=10, range=None, density=None, weights=None)【numpy.histogram()のパラメータ】
●a(array_like):配列・データ
●bins(int or sequence of scalars or str, optional):階級値の数
●range((float, float), optional):階級(bins)の上限・下限
●weight(sarray_like, optional):deinsity=Trueの時は正規化され、積分時の総面積が1となる
●density(bool, optional):Falseなら各階級(bin)の度数を出力し、Trueなら確率密度関数を出力する
【出力】
●hist(array):ヒストグラムが出力
8-1-3.相対度数と確率密度
本項では「ヒストグラムにおける相対度数」と「確率密度分布における確率密度」の違いを説明します。なお内容は下記記事を先取りしています。
ヒストグラム(階級vs度数の分布)の度数を全データ数で割ると相対度数を得られますが、「相対度数と、確率密度分布における確率密度は別物」ということです。
$$
確率密度関数 f(x) \geq 0, \hspace{20px} \int_{-{\infty}}^{\infty} f(x)dx = 1
$$
$$
確率変数 P(a \leq x \leq b) = \int_a^b f(x)dx
$$
ヒストグラムは柱を分割することができ階級の区切りが見えないほど細かくすると確率密度関数になります。

サンプルデータとして「e-Stat 国民健康・栄養調査」->「2018年における30-39歳の平均身長μ=172.1cm, 標準偏差σ=6.1cm」を元に計算します。
まずはベースのデータと関数を用意しました。まずはScipyを用いて理論的な正規分布を出力しました。確かに正規分布の式から得られる値とあっていることが確認できました。
[IN]
#2018年の30-39歳の男性の平均身長 https://www.e-stat.go.jp/dbview?sid=0003224177
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from typing import List
from scipy import stats
import os
np.random.seed(12)
#正規分布確認用
def norm(x, mu, sigma):
return 1/(sigma*np.sqrt(2*np.pi))*np.exp(-(x-mu)**2/(2*sigma**2))
def showGraph(xs: List, ys: List, labels: List, verbose=False):
fig = plt.figure(figsize=(10, 6), facecolor='w')
ax = fig.add_subplot(111)
colors = {0:'red', 1:'blue', 2:'green', 3:'orange'}
idx = 0
#確率密度分布
for x, y, label in zip(xs, ys, labels):
#分布を表示
ax.plot(x, y, label=label, color=colors[idx])
if idx == 0:
mean, std = 172.1, 6.1
sigma1_low, sigma1_high = mean-std, mean+std
sigma2_low, sigma2_high = mean-2*std, mean+2*std
y_sigma1_low = stats.norm.pdf(sigma1_low, loc=mean, scale=std) #正規分布
y_sigma1_high = stats.norm.pdf(sigma1_high, loc=mean, scale=std) #正規分布
y_sigma2_low = stats.norm.pdf(sigma2_low, loc=mean, scale=std) #正規分布
y_sigma2_high = stats.norm.pdf(sigma2_high, loc=mean, scale=std) #正規分布
#標準偏差を表示
ax.plot([sigma1_low, sigma1_low], [0, y_sigma1_low],
color='red', linestyle='--', lw=1, label='1σ')
ax.plot([sigma1_high, sigma1_high], [0, y_sigma1_high],
color='red', linestyle='--', lw=1, label='1σ')
ax.plot([sigma2_low, sigma2_low], [0, y_sigma2_low],
color='red', linestyle='-.', lw=1, label='2σ')
ax.plot([sigma2_high, sigma2_high], [0, y_sigma2_high],
color='red', linestyle='-.', lw=1, label='2σ')
idx += 1
#体裁調整
ax.set(xlabel='平均身長', ylabel='確率(比率)',
xticks=np.arange(140, 200+5, 5))
plt.title(f'正規分布(2018年の30-39歳の男性の平均身長)', y=-0.15)
plt.grid()
plt.legend()
if verbose:
if os.path.exists('image') == False:
os.mkdir('image') #imageフォルダがなければ作成
plt.savefig(f'image/確率密度_{label}.png')
plt.show()
#確認用
mean, std = 172.1, 6.1 #平均値μ, 標準偏差σ
print(f'平均値の確率:標準正規分布:{norm(0, 0, 1):.2f}, 本試験:{norm(mean, mean, std):.3f}') #標準正規分布の確認
x_population = np.arange(140, 200, 1) #x軸の値を計算
y_population= stats.norm.pdf(x_population, loc=172.1, scale=6.1) #確率密度関数
showGraph([x_population], [y_population], ['標準正規分布'])
[OUT]
平均値の確率:標準正規分布:0.40, 本試験:0.065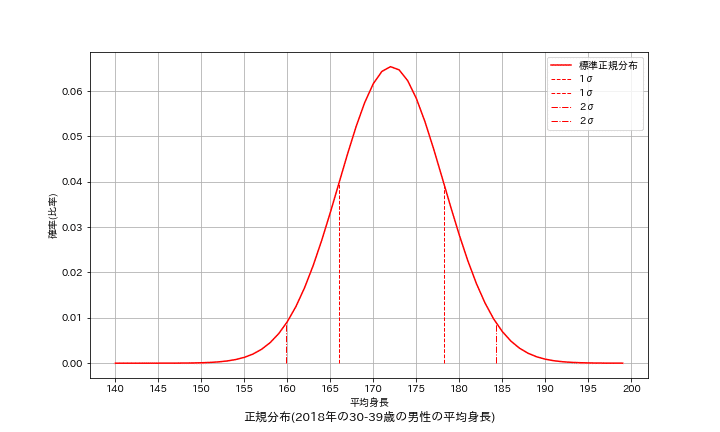
$$
正規分布f(x)=\dfrac{1}{\sqrt{2\pi\sigma}}\exp(-\dfrac{(x-\mu)^ 2}{2\sigma^ 2})
$$
まずヒストグラムから相対度数の分布を作成します。具体的には「ヒストグラムの高さをすべてのデータ数で割る」処理をします。結果を見るとbinsが増えるごとに山は小さくなり、かつ正規分布の確率密度分布の形状とも異なります(平均値は同じため正規分布の計算式に従っていない)。
$$
相対度数=\frac{度数}{サンプル数}
$$
[IN]
#母集団の作成
mean, std = 172.1, 6.1 #平均値μ, 標準偏差σ
nums_p = int(1e6) #乱数値用に大きなサンプルサイズnを指定
datas_p = np.random.normal(mean, std, size=nums_p)
freqs1, _x1 = np.histogram(datas_p, bins=30)
freqs2, _x2 = np.histogram(datas_p, bins=100)
freqs3, _x3 = np.histogram(datas_p, bins=1000)
#相対度数の計算(確率密度ではない)
freq1_rel = freqs1 / nums_p
freq2_rel = freqs2 / nums_p
freq3_rel = freqs3 / nums_p
x1, x2, x3 = (_x1[1:] + _x1[:-1]) / 2, (_x2[1:] + _x2[:-1]) / 2, (_x3[1:] + _x3[:-1]) / 2 #x軸の値を計算
print(f'形状確認:{freqs1.shape}, {freqs2.shape}, {freqs3.shape}, {freq1_rel.shape}, {freq2_rel.shape}, {freq3_rel.shape}')
print(f'合計値の確認 : {freq1_rel.sum():.3f}, {freq2_rel.sum():.3f}, {freq3_rel.sum():.3f}')
xs, ys, labels = [x_population, x1, x2, x3], [y_population, freq1_rel, freq2_rel, freq3_rel], ['標準正規分布', 'bins30', 'bins100', 'bins1000']
showGraph(xs, ys, labels, verbose=True)
[OUT]
原因としては下記の通りです。
確率密度分布$${f(x)}$$は積分した範囲が確率になるのに対して、相対度数度数をプロットした関数は高さの合計が1になる。
確率密度分布は「全区間の積分値が1」であり値の合計値は1を超えることもある(確率密度分布は値の合計値には意味がない)
相対度数を確率密度関数へ変更するには下記3種の方法があります。
度数を「すべてのデータ数 × ヒストグラムのビンの幅」で割る
Numpyの「np.histgram(density=True)」とする。
Matplotlibの「plt.hist(density=True)」とする。
$$
確率密度f(x)=\frac{度数}{サンプル数×階級値(bins)の幅}
$$
計算より下記が確認できました。
各種手法で相対度数から確率密度分布(関数)を表現できた
確率密度関数の合計値は1を超える(合計値そのものには意味がない)
[IN]
#母集団の作成
mean, std = 172.1, 6.1 #平均値μ, 標準偏差σ
nums_p = int(1e6) #乱数値用に大きなサンプルサイズnを指定
#標本1
datas_p = np.random.normal(mean, std, size=nums_p)
p_dense1, _x1 = np.histogram(datas_p, bins=30, density=True)
#標本2
freqs2, _x2 = np.histogram(datas_p, bins=100)
bin_width = _x2[1] - _x2[0] #階級幅
p_dense2 = freqs2 / (nums_p * bin_width) #確率
x1, x2 = (_x1[1:] + _x1[:-1]) / 2, (_x2[1:] + _x2[:-1]) / 2#x軸の値を計算
print(f'形状確認:{p_dense1.shape}, {p_dense2.shape}, {freq2_rel.shape},')
print(f'合計値の確認 : {freq2_rel.sum():.3f}, {p_dense2.sum():.3f}')
xs, ys, labels = [x_population, x1, x2], [y_population, p_dense1, p_dense2], ['標準正規分布', 'bins30', 'bins100']
showGraph(xs, ys, labels, verbose=True)
[OUT]
キーワード一覧
推測統計:母集団から抽出した標本の情報を用いて、母集団の情報を推測する。統計学的に推測するには、データに当てはまるであろう確率分布を推定し、その確率分布を基に、母集団のデータを推測します。
度数分布表:データを複数の区間に分割して、それぞれの区間にいくつデータが存在するかを調べ上げた表であり、この表を基にヒストグラムを作成する。
大数の法則(law of large numbers):ある独立した試行においてその事象が発生する確率をpとすると、試行回数nが大きくなるにつれて事象の発生確率がpに近づいていくこと
中心極限定理:母集団が正規分布でなくても、そこから抽出したサンプルサイズNが大きくなると標本の分布は正規分布に近づく
モンテカルロ法:、乱数を用いた試行を繰り返すことにより近似解を求める手法->大数の法則を考慮すると試行回数nを大きくして近似解を取得
シンプソンのパラドックス:データの母集団全体における相関と、その母集団を分割した一部の集団における相関は必ずしも一致しない
チェビシェフの不等式:正規分布でなくても一般的に標準偏差のk倍離れた値は$${\frac{1}{k^2}}$$以下である。
因果推論:入力データ(インプット)と出力データ(アウトプット)から、その因果関係(原因とそれによって生じる結果との関係)を統計的に推定していく考え方のこと
$$
チェビシェフの不等式:P(|x-\mu|\geq k\sigma) \leq \frac{1}{k^2}
$$
参考資料
理論用
http://www2.econ.osaka-u.ac.jp/~tanizaki/cv/books/stat3.pdf
Python用
データ用
あとがき
追って追記予定
