
【人民元の国際化とは?🤔】関税競争ゲームから考察する貿易均衡実現メカニズム🎊:日経新聞解説📰 2023/07/26
日本経済新聞の記事で
注目したい内容がありましたので
記事にしたいと思います💖
長いですが、目次をご活用いただきまして
どうぞ最後までご覧ください!
中国相手の貿易・資本取引決済 人民元、初のドル超え 4~6月、対ロ制裁も影響
中国が取引相手となる2国間決済で、中国の通貨・人民元の利用が広がっている。
企業や機関投資家などによる決済通貨を集計したところ、人民元建ての割合は2023年4~6月期に49%となり、初めて米ドル建てを上回った。
金融開放やロシアとの取引拡大の影響が大きい。世界全体の決済では人民元比率は3%弱にとどまるが、「ドル離れ(総合2面きょうのことば)」が進み始めた。
中国国家外貨管理局が公表する統計資料を基に、企業や個人、投資家の越境(クロスボーダー)取引を通貨別に集計した。
貨物やサービス、経常移転などで構成する貿易決済に加え、株式や債券の売買など資本取引決済が含まれる。
今回の集計には中国を直接介さない第三国間の貿易・資本取引の人民元決済は含まれていない。
国際銀行間通信協会(Swift)によると、世界全体の決済額シェアは23年6月時点で米ドルが42.02%と首位、人民元は2.77%で5位だ。
世界の国内総生産(GDP)に占める中国の割合に比べて、人民元決済の世界シェアはまだ少ない。
ただ約5年前の1.81%からは上昇しており、存在感が徐々に高まっている。その原動力が中国の経済力を背景にした2国間決済だ。
23年4~6月期の人民元建て越境決済額は前年同期比11%増の1兆5104億㌦(約211兆円)。
遡れる10年以降のデータを見る限り、四半期ベースで人民元が米ドルを上回るのは初めてだ。
人民元建て決済の拡大は①資本市場の解放、②貿易決済における「脱ドル化」――の2つの要因がある。
中国政府は外国人による本土での人民元建て金融取引を厳しく制限する一方、金融都市としての存在感を高める狙いもあって香港経由では株式や債券取引をできるようにしてきた。
貿易金融ではロシアとの人民元取引拡大が影響している。
ロシアは22年のウクライナ侵攻後、米欧日の金融制裁でドルやユーロの決済網から締め出され、中国との原油取引に人民元を使う。
今後も人民元決済のシェアは高まる可能性が高い。中国政府によって人民元の国際化を強化する方針が示されたからだ。
22年10月の中国共産党大会で、習近平(シー・ジンピン)総書記は人民元の国際化を「秩序だって進める」と発言し、従来方針である「着実かつ慎重に進める」に比べて、より積極性が増した。
中国政府は相次ぎ2国間協定の締結に動いた。
南米ブラジルとは3月、大豆の主要輸出先である中国との貿易や投資で、米ドルを介さずに人民元とレアルを交換することで合意した。同じくアルゼンチンは4月、中国からの輸入品の決済を米ドルから人民元に切り替えると発表した。
多くの新興国は為替取引で米ドルへの依存を減らしたいと考えている。
米国がドルの支配的な地位を使ってロシアに金融制裁を実施し、一部の国々が「脱ドル」を考える契機となった。
人民元は相場変動を避けるため国際送金で厳しい規制がある。習指導部は国際化と通貨安定のバランスを取りながら段階的に規制緩和を進めていくとみられる。
(上海=土居倫之、秋田咲)
記事に対するコメント📝
中国が取引相手となる2国間決済で
中国の通貨・人民元の利用が拡大している
という日経新聞一面の記事について着目します
企業や機関投資家などによる決済通貨を
集計したところ、人民元建ての割合は
2023年4~6月期に49%となりました
これは、初めて米ドル建ての決済通貨額を
上回ったということがファクトとして判明しました
考えられる理由としては金融開放やロシアとの取引拡大の影響が大きい、ということですね📝
多くの新興国は為替取引で米ドルへの依存を減らしたいと考えているそうです
米国がドルの支配的な地位を使ってロシアに
金融制裁を実施し、一部の国々が「脱ドル」を考える契機になっていることは事実ですね
ただし、人民元は相場変動を避けるため国際送金で厳しい規制があります
これから中国が、本当に世界の覇権国となるのであれば、国際化と通貨安定のバランスを取りながら段階的に規制緩和を進めていくことが必要になることに異論はないと思います
関税率と貿易均衡価格との関係
以下では、関税と貿易均衡についてより考察していくことにしましょう
A国の関税率 τ^A が与えられるとA国のオファーカーブが確定し、B国の関税率 τ^B が与えられるとB国のオファーカーブが確定することになります

両オファーカーブの交点が貿易均衡
貿易均衡価格決定(第1財相対価格)が決定されるのです
$$
Trade Equilibrium Price\\
p^* (\tau^A, \tau^B)…➀\\ \\
\frac{\partial p^* (\tau^A, \tau^B)}{\partial \tau^A}<0,\frac{\partial p^* (\tau^A, \tau^B)}{\partial \tau^B}>0
$$
A国は、第1財の輸入国
B国=第2財の輸入国であるとしたらならば、貿易均衡価格は、A国の関税に関して減少、B国に関して増加となります
関税効用関数の導入
A,B両国の関税率が与えられると、世界価格が定まります
よって、これに対応して各国の国内価格が確定することになるのです
そして、各国の国内価格に対応して、生産点(y)、所得水準、消費点(x)が定まりますので、各国の経済厚生も確定することになるのです📝
このような過程から、各国の経済厚生は関税率の組の関数とし
て表されることがわかるのです
これを以下のような関税効用関数として定義しましょう
$$
Tariff Utility Function\\
W^k(\tau^A,\tau^B) , k=A,B \\ \\
\frac{\partial W^A (\tau^A, \tau^B)}{\partial \tau^A}>0,\frac{\partial W^A (\tau^A, \tau^B)}{\partial \tau^B} < 0
$$
関税効用関数は、原点(0,0)の点において自国の関税率に関し
て増加的です
自由貿易を行っている状況からの一方的な関税率引き上げによって当該国の経済厚生は、改善することになります👍
なお、貿易相手国の関税率がゼロならば、ある正の自国関税率の
下で関税効用関数は最大となります
このときの税率こそ、最適関税率に他ならないのです
また、関税効用関数は、貿易相手国の関税率に関して減少的です
理由は、外国の関税引き上げは自国にとって不利だからです
そして、関税効用関数の値を一定に保つような関税率の組を図解し
たものを「関税無差別曲線」と呼ぶことにし、以下のような図解を用いてイメージし、理解を深めたいと思います

原点O点は、両国が自由貿易を行っている状態です
B国の関税率が0のとき、A国の経済厚生を最大にするのは
A国が一方的に最適関税τ^Aを施すときになるのです
関税競争ゲームのモデル分析🌟
以下では、国際貿易論においてかなり面白いテーマである「関税競争ゲーム」について考察します
登場するプレイヤーは、A国政府とB国政府です
実行する戦略として各国は関税率を操作します
このゲームから得る利得は、各国の関税効用関数によって評価することにします
ここで、このモデルのキーポイントなのですが、各国が有する相手国の関税率に対する
関税反応関数について言及したいと思います
関税反応関数とは、貿易相手国の所与の関税率に対して、自国の効用関数の値を最大にするような自国関税率を対応させる関数のことを指します
それでは、関税競争ゲームを以下のように定式化します
$$
Tariff Competition Game\\ \\
Player: Govment A, B\\
Strategy:\tau^A,\tau^B\\
Profit: W^k(\tau^A,\tau^B) , k=A,B
\\ \\
Tariff Response Function\\ \\\tau^k = \psi^k(\tau^l) \\\equiv\arg\displaystyle\max_{\tau^k}W^k(\tau^A,\tau^B)\\
k,l = A,B ;k\not=l\\
$$
それでは、以下に関税反応関数を図解して、よりイメージを膨らませていくことにしましょう
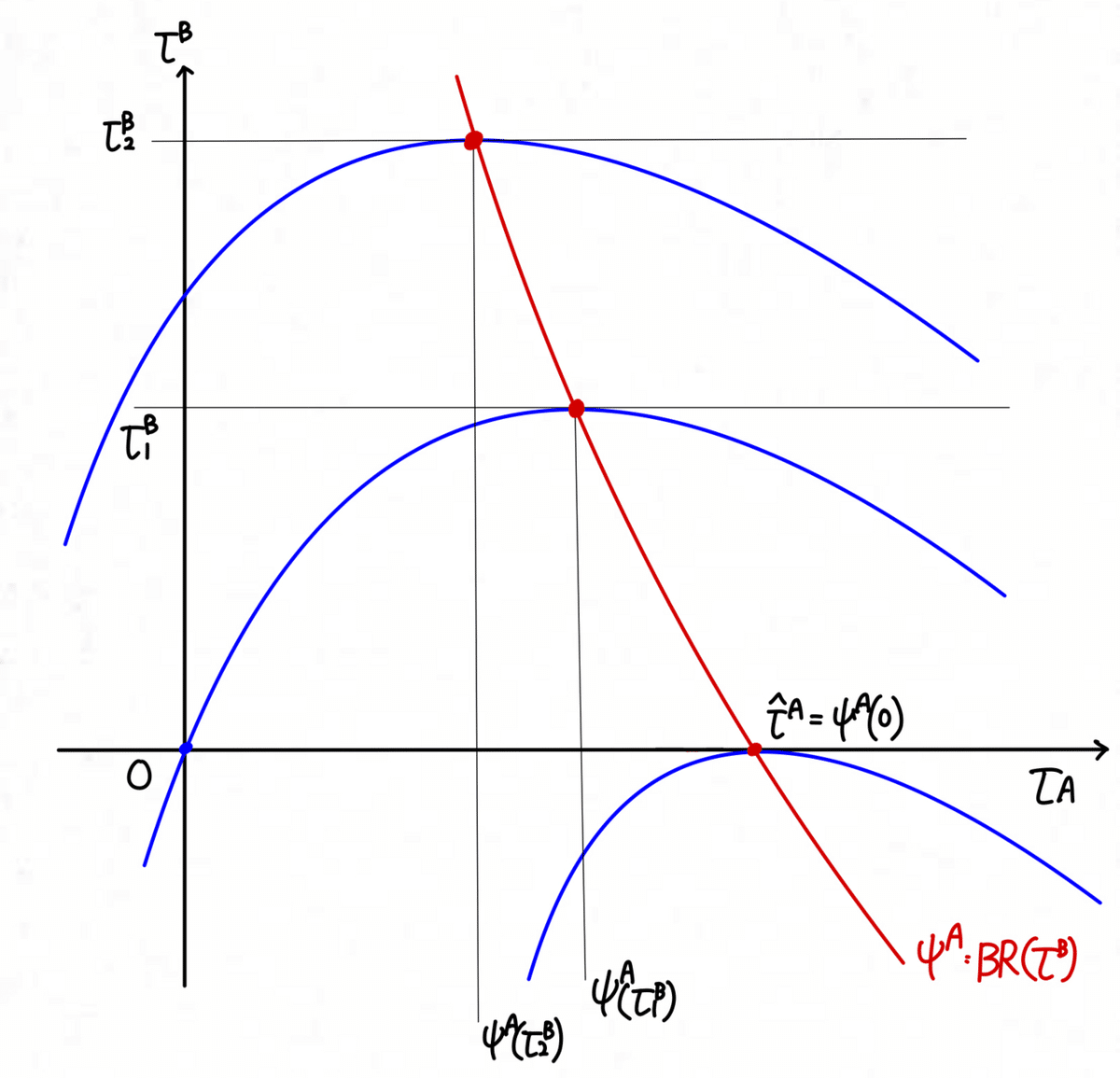
関税反応曲線は、図において赤線で示されており、貿易相手国の関税率に対応する自国の経済厚生を最大にする点を並べた曲線であることを確認します
ナッシュ関税均衡✨
両国が,それぞれ単独では関税率を変更する誘因をもたない関税率の組合わせを「関税競争ゲームのナッシュ均衡」と呼ぶことにします
簡潔に「ナッシュ関税均衡」とも言います
$$
Nash Tariff Equilibrium\\ \\
W^A(\tau^{A^*},\tau^{B^*})\geq W^A(\tau^A,\tau^{B^*}) \forall \tau^A\\ \\W^A(\tau^{A^*},\tau^{B^*})\geq W^B(\tau^{A^*},\tau^{B}) \forall \tau^B \\ \\Or, intersection of \\Best Tariff Responce Function\\ \\\tau^{A^*}=\psi^A(\tau^{B^*})&\tau^{B^*}=\psi^B(\tau^{A^*})
$$
以下でも同様に、ナッシュ関税均衡の図解を用いてイメージしていきたいと思います

ナッシュ関税均衡に対応する関税率の組より、両国が同時に関税
率を引き下げると両国の経済厚生は改善する(=パレート改善)ことになります
つまり、ナッシュ関税均衡はパレート効率ではないというインプリケーションを得ることになるのです
ナッシュ関税均衡の性質
ナッシュ関税均衡となる関税の組み合わせにおいて、両国の関税無差別曲線は互いに直交していることがわかります
両国の関税率を同時に引き下げれば、両国の厚生は同時に改善する(=パレート改善)ことになりますので、ナッシュ関税均衡はパレート効率的ではないことがわかります
ジョンソンの場合:Johnson’s case
先の図解では、ナッシュ関税均衡における両国経済厚生は自由貿易 の場合よりも低いケースを図示しました
これは、A国政府とB国政府が関税競争ゲームをした結果、共倒れしてしまった状態ということになります
しかし、ナッシュ関税均衡において、どちらか一方の国が自由貿易の場合よりも高い効用水準を実現する可能性は理論的にありうるのです
これは「ジョンソンの場合:Johnson’s case」と呼ばれています📝

若干の注意点📑
先に示したナッシュ関税均衡となる関税率の組み合わせにおいては正の貿易取引が行われていることにご留意ください
「ジョンソンの場合」でも同様です
ただし、正の貿易取引を伴うナッシュ関税均衡が存在するとは限りません
なお、正の貿易取引を伴うナッシュ関税均衡が存在しても、その均衡点が一意的に定まるとも限らないのです
また、両国の関税において、貿易取引が行われなくなるほどの高関税率を「禁止的関税率」といいます
両国の禁止的関税率の組も関税競争ゲームのナッシュ均衡のひとつであり、この均衡点は必ず存在すると言われています
なお、禁止的関税率となる組み合わせの下での両国の効用水準は自由貿易の場合よりも低くなります
これは、鎖国状態と同じですね
国際貿易における関税政策など、どのような基準や視点から政策評価をするのか、通時的な判断によってメリットがデメリットを上回っているのか、ということなど考慮すべき点がたくさんありますね
経済学を学ぶなかで、このような多角的な視点をもって考察する力を醸成することができると思いますので、今後も一生懸命取り組んでいきたいと思います💖
本日の解説は、以上とします✨
またこのような貿易のニュースをもっと楽しく理解できるようになれば、きっと見える世界が広がるのではないでしょうか?🥺
マガジンのご紹介🔔
こちらのマガジンにて
エッセンシャル経済学理論集、ならびに
【国際経済学🌏】の基礎理論をまとめています
今後、さらにコンテンツを拡充できるように努めて参りますので
今後とも何卒よろしくお願い申し上げます📚
最後までご愛読いただき誠に有難うございます!
あくまで、私の見解や思ったことを
まとめさせていただいてますが
その点に関しまして、ご了承ください🙏
この投稿をみてくださった方が
ほんの小さな事でも学びがあった!
考え方の引き出しが増えた!
読書から学べることが多い!
などなど、プラスの収穫があったのであれば
大変嬉しく思いますし、投稿作成の冥利に尽きます!!
お気軽にコメント、いいね「スキ」💖
そして、お差し支えなければ
フォロー&シェアをお願いしたいです👍
今後とも何卒よろしくお願いいたします!
