数学のセンスはあるらしい

息子は日本語を操るのは苦手だが、数字は好きで算数も比較的得意だ。
ざっくり言うと、国語は小1レベルの文章がやっと読める程度だが、算数は小5で習う平均や割合の問題にも取り組んでいるという凸凹っぷり。

そんな息子は、「カレンダー」や「アルファベット表」といった文字や数字が規則的に並んでいる表や図が好きだ。
その流れで、「十二支」も好きで、12年周期で規則的に進んでいくというのがいいらしい。

今年は2024年。
4年に1度のうるう年ということで、彼の中でちょっと盛り上がりを見せている。

「2月と3月はいつも同じ曜日から始まるけれど、今年は1日ズレる」
「1/1と12/31はいつも同じ曜日だが、今年は1日ズレる」

という変化が面白いみたいだ。
そんな中で、彼は、

「うるう年は、必ず、ねずみ年かたつ年かさる年のどれかである」

という法則を自分で見つけた。
これには私も夫も「へー！」と驚いた。
干支とうるう年を結びつけて考えたことなどこれまで無かったからだ。
4年に1回だし、干支は4の倍数である12年周期だから確かにそうなる。
立派な「定理」だ！

先日、数学科卒の夫が出身大学の指導教員に久しぶりに会う機会があった。
そのときに上記の話をしたら、
「それはセンスあるね」
と言ってくれたそうだ。
大学教授のお墨付きだよ息子！笑
そしてこんな面白い法則を先生から教えてもらったとので、おはなしメモを使って息子に伝えてみた。

正確には「うるう年でなければ」の条件は要らない

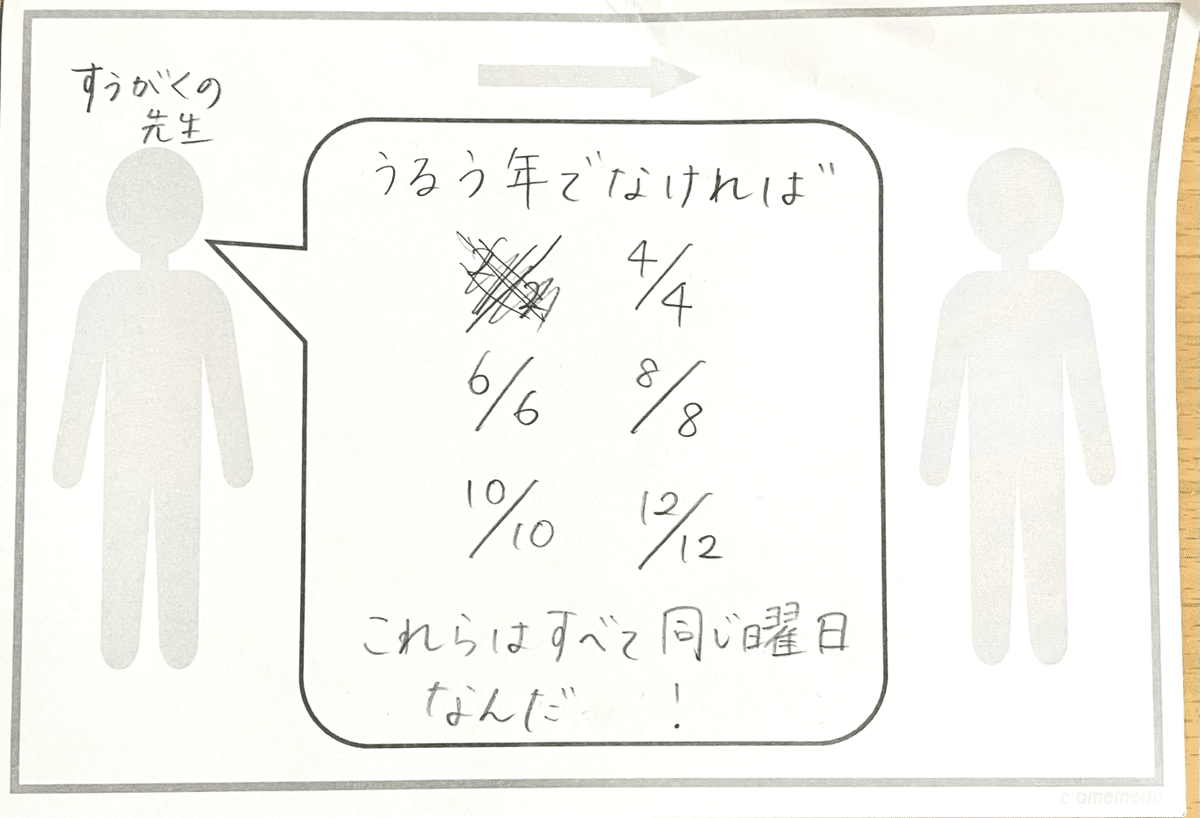
4/4〜6/6、6/6〜8/8… はすべて7の倍数である63日間だから確かにそう。
息子はさっそく、2020年〜2025年のカレンダーをニコニコしながら眺めて確認していた。

息子の注目する点は、数字に限らず、地味で些細な点である場合が多い。
毎回「よくそんなとこ見てたね！」と思うし、
いかに自分が雑にしか物事を見ていないかを思い知らされる。
小さな変化に気づくことができ、規則性を見つけることが好きな彼には、大きな変化やサプライズは刺激が大きすぎる。
彼にとって、身近な世界にはすでに驚きと不思議で満ちているのだから。
「息子と一緒に生活していると、世界を見る時の解像度が上がる」と私はよく言うのだが、それはこういうことでもあるのだ。