
モンティ・ホール問題について教えていたら初等確率論のエッセンスを再発見した。
モンティ・ホール問題という有名な数学の問題がある(ここ数年で急に有名になった気がするのは私だけでしょうか)。改めて説明するまでもないかもしれませんが、こんな問題。
あなたの目の前に3枚の扉があり、そのうち1つだけに「当たり」の扉がある。
さて、あなたは「当たり」の扉を開くべくいずれか一つの扉を選択したのだが、その扉を開く前に扉の「管理人」があなたの選択しなかった扉の一つを開いたところ、その扉は「当たり」でなかった。
さて、あなたはここで開く扉を変更してもよいのだが、変更するべきだろうか。
変更するべきだろうか、というのはつまり、変更した方が「当たり」の扉を開く確率が高いだろうか、変わらないだろうか、低いだろうか、と言っても良いでしょうね。
誤解なく問題が伝わってるでしょうか。少し具体的に述べましょう(知ってるよ!という方は少し下にある回答のところまでスクロールしてください。長い空白のすぐ後のところです)。
例えば、3枚の扉を適当に左からA,B,Cと名付けたとしましょう。その扉のいずれか1つの扉の向こうには賞金があるとでも考えましょうか。
あなたが真ん中のBの扉を選択し、開こうとしたところ、「管理人」がAの扉を開き、賞金がないことを示してみせました(この「管理人」はどの扉が賞金につながるかを知っているとします)。
さて、ここであなたはBの扉ではなくCの扉を開いても構わないのですが、どちらの扉を開く方がよいでしょうか?
つまり、
・開く扉を変更する(最初に選択したBの扉を開く)べきか、
・変更しない(やっぱりCの扉を開く)でおくべきか?
という問題ですね。
初めてこの問題を見た方、そして自分の頭で考えてみたい方(もしいれば!)のために回答は少し下の方に書いておきましょう。
回答:「変更した方がよい」=「変更した方が「当たり」の扉を開く確率が高い」
でした!(知ってたって?)
さて。ここから少し個人的な話(回答に納得できないんだけど、、という方も少しお付き合いください)。
数学やパズルに興味のある方には有名すぎる問題ですが、まだまだこの問題を知らない/よく分かってない方は多いようで、先日、そんな友人の相手をしていました。どうにも回答に納得出来ないそうです(そんな人が多いからこそ語り継がれる名問なわけで)。
そこで、私としてはあの手この手でその友人にこの回答について納得させようとするわけですね。
説明1.
最初に3枚の扉の内から1つの扉(Bとしよう)を選んだ時点で、Bが当たりである確率は1/3で間違いない。
裏を返せば、Bが外れである確率=AまたはCの扉があたりである確率は2/3であり、「管理人」が他の扉(Aとしよう)を開くことで、Cの扉が当たりである確率にこの2/3という値が集約する。
この説明は問題の本質を端的に言い表しています。が、これで正しく納得できる人は、おそらく既にちゃんと理解している人だけで、多くの人はいまいち納得出来ないと思います。友人もそうでした。
また、この理屈を無闇に(よく理解せず)確率の問題について適応するのは誤答を導く可能性も高く、危険です。
ではこんな説明ではどうでしょうか。
説明2.
数を拡大してみる。
つまり、100枚の扉(当たりは1つだけ)の中から1枚の扉を選ぶ。それ以外の99枚の扉のうち(1枚を残し)98枚が空であることが示された後に変更するべきだろうか?
明らかに、変更した方が当たる気がしないだろうか?
今まで納得出来なかった人も、この説明で腑に落ちる人は意外と多いようです。
定性的・直観的な理解のためにスケールを変更してしまうというのは便利な手法ですね。
しかし、厄介なことに友人はこの説明でもいまいち納得しませんでした。
曰く、「100枚の扉で試行すれば変更した方がいいというのはなんとなく分かる気もする。ただ、100枚でそうだからといって、3枚でもそうとは限らない。」とのこと。少し痛いところをついてきますね。先程の説明は定性的な部分に焦点を絞っているため、この手の批判には少し弱いです。
逆に言えば、定量的な部分の理解を補う段階まで来たとも言えます。
となれば、最終手段です。
説明3.
全部、書き出してみよう
古典的で最も確実な方法の一つですね。
そして、この話のキモの部分でもあります。
書き出してみよう
確率の問題を考える上で、考えられるパターンを全部書き出してしまうというのは、パターンがあまりにも多すぎる場合や時間が限られている場合(試験中とか!)を除いては、単純ゆえに効果的な方法の一つです。
特に、今回のモンティ・ホール問題では扉が3枚しかないため、かなり簡単にこの方法が使えるようですね。
などなど述べた上で、そのとき友人に示した図の概形は以下のようなものでした(図1)。

かなりシンプルな樹形図ですね。たった9パターンしかないし。
少し補足を。
『変更すべきか否か』という項目は、変更した方が可能性が高くなるか、という意味ではありません。各パターンについては変更することで当たるかどうかがハッキリしているためです(問題の中の『あなた』は知り得ませんが)。
“「当たり」の扉”と“最初に選んだ扉“が一致しているのであれば、もちろん、その後に選択を変更することで、必ず「当たり」の扉を開けられなくなります(図ではこれを×で表現しています)。
“「当たり」の扉”と“最初に選んだ扉“が一致していないのであれば、その後に選択を変更することで、必ず「当たり」の扉を開けられるようになります(図ではこれを○で表現しています)。
なぜならば、この場合、最初に選んでない扉2つのいずれかが「当たり」の扉であり、「管理人」が空の扉を開いた後に残っている扉が「当たり」であることが明白だからです。
この辺りについて考えると、「管理人」の介入がこの問題をややこしくしている元凶であることがよく分かってくるので、是非理解を深めてください。
図1を見れば、変更することで「当たり」を引く確率が2/3、変更しないことで「当たり」を引く確率が1/3であることがよく分かるのではないでしょうか(説明1.に納得できなかった人はこれを踏まえて見返してみてください!)。
ところが。友人はこの説明を受けてなお反論してきたのです。
というのも、「管理人」が開く扉について考慮すべきでないのか?
つまり、より適切な樹形図は以下のようなものではないか?と(図2)。
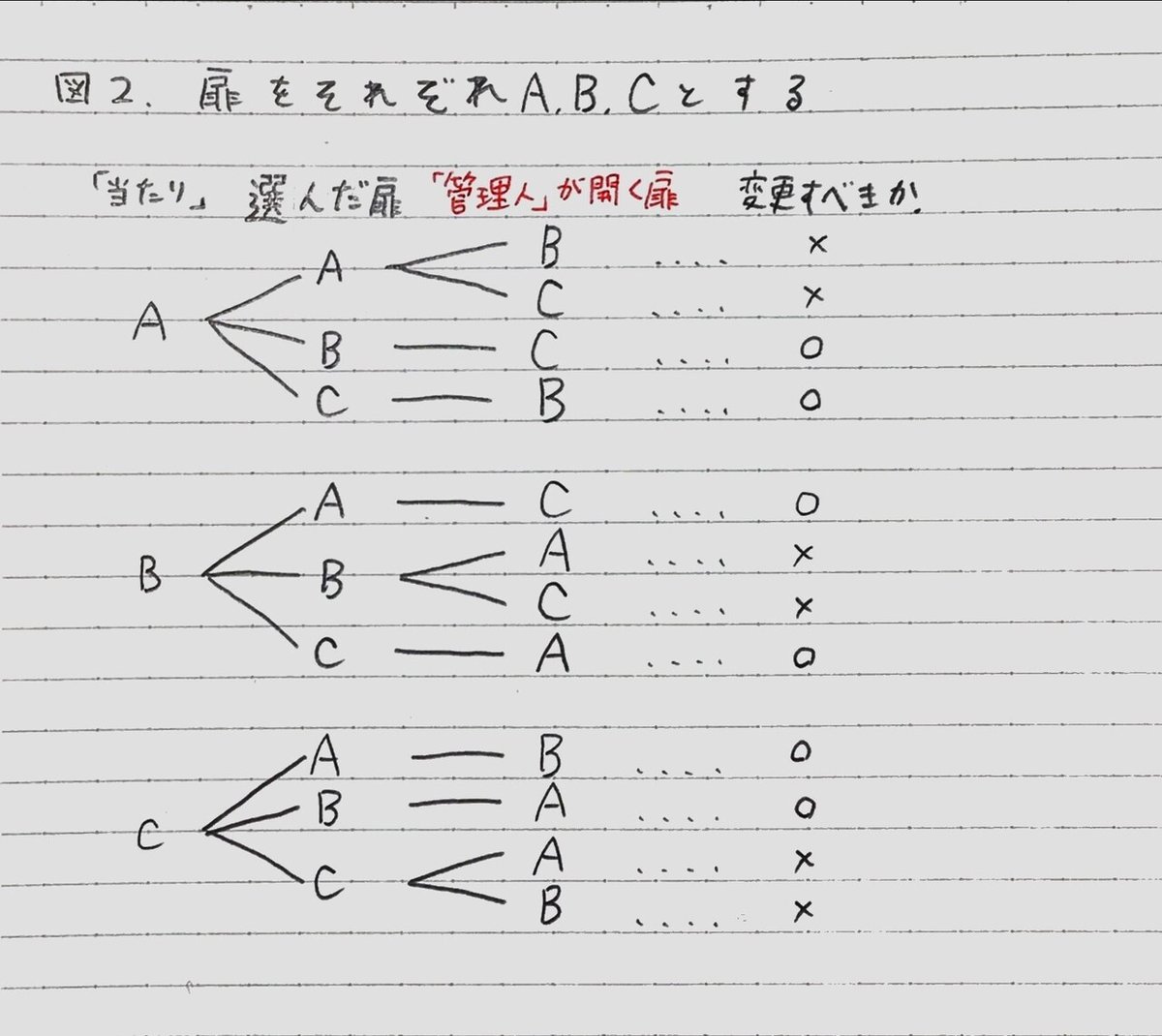
少しややこしく見えますが、図1に“「管理人」が開く扉“という項目を追加しただけ、と思っていただければいいと思います。
図1に比べて各項目の名称を少し端折ってますが、問題ないでしょう。
これも補足を。
問題より、「管理人」の開く扉は、選択されていない扉のうち「当たり」でないものです(必要十分条件)。
たとえば、Aの扉が「当たり」でかつ選ばれていた場合、「管理人」はBの扉を開いてもCの扉を開いても構いません(上から1つ目、2つ目のパターン)。
Aの扉が「当たり」でBの扉が選ばれていた場合、「管理人」はCの扉を開かなければなりません(上から3つ目のパターン)。
同様に考えていけば図2のようになるはずです。
さて、図2を見ると、変更することで「当たり」を引く確率も、変更しないことで「当たり」を引く確率も等しく1/2である導ける…いや、図1によると変更した方が「当たり」を引きやすいはずでは…
さて、困ったことになりました。
実際、この問題に気づいた時、私は恥ずかしながらどこで間違えているかがいまいち分からず、5分ほど考え込んでしまいました。
本当に混乱してしまいそうな人のために述べておくと、やはりモンティ・ホール問題の解答は「変更した方がよい」で間違いありませんし、確率の値も理論的には図1から求めた通りです。
ではどこに落とし穴があったか?
数学に自信のある方は是非読み進める前によく考えてみてください。そんなに難しいことではありません。
箸休め的に余談を。
note内ではスムーズに話を進めていますが、実際に友人と対話していた際はここまですんなりと事は運びませんでした。というのも、友人は常に感覚的な違和感について自分なりに話してくれるため、その主張を数学的な表現に落とし込むのに労力を費やすことになりました。
特に苦戦したのは図2の樹形図を書くときで、あれは友人が自身のイメージを書き出してくれたのではなく、友人の述べる違和感を汲み取って自分で書き出したものです。
また、実際に対話していた時はもっと雑で汚いメモを使っていたので、ここに載せているものはルーズリーフに清書したものです(それでも字が汚くてお見苦しいかもしれませんが…)。
場合の数と確率
私の記憶が正しければ、中学高校では確率の単元は主に「場合の数と確率」として、場合の数とセットで扱われていたと思います。図1や図2に代表される樹形図も、元々は場合の数で扱われていたものだった気がします。
中高で勉強された事のある方なら、なぜ「場合の数と確率」はまとめて扱われるか、なんとなく分かると思います。この二つの単元は親和性が高く、場合の数を理解することで確率を求められるようになるからですね(説明3.でやろうとしたように)。
では逆に、なぜ「確率と場合の数」は二つの単元に分けられるのでしょう?
確率と場合の数は何が違うのでしょう?
まあ、何が違うのでしょう?とか言っても全然違うのですが、一つの回答として、初等確率論には、それを考える上でものすごーく重要な概念、「同様に確からしい」がある、という回答が考えられます。
勘の良い方ならお気づきだと思いますが、この「同様に確からしい」こそが、先の混乱の落とし穴です。
図2の樹形図を見ると確かに、16のパターンの内変更すべきパターンと変更すべきでないパターンが8パターンずつで差がないように見えます。しかし、確率の問題としてこれを捉えるうえでは、この16のパターンが総て「同様に確からしい」かをきちんと考える必要があったのです(そうでなかったわけですが)。
少し細々とした、正直あまり上手いと思えていない説明になるので補足だと思ってください。
図2の樹形図で示されている16のパターンが同様に確からしくないのは、「当たり」の扉と選択した扉が一致している場合とそうでない場合について考えてみると分かるかと思います。
前者について、管理人が開く扉は二通りあります。が、どちらを選んでもいいわけで、ここで新たにランダムな要素が入り込みます(どちらを選ぶかは五分五分である、のような)。
後者について、管理人が開く扉は一通りに定まっており、ランダムな要素はありません。
図2の樹形図ではこれらをまとめて並列に扱っていたため、公平でなかったと言えるわけですね。「管理人」の介入が問題をややこしくしている、というのも少し分かるような気がしないでしょうか。
もちろん、図1の樹形図の9パターンについても「同様に確からしい」かどうかを考える必要があります。こちらは実際に「同様に確からしい」ですね。
「同様に確からしい」かどうかを見分けるにはどうすればよいか?をキッチリと述べておきたかったのですが、どうしても長くなってしまう上、上手い説明ができる自信もないので、ここで締めに入りたいと思います。
拙文ながら、「同様に確からしい」について考えることが初等確率論において非常に重要ということが伝わっていれば幸いです。
友人と話している時はここまで深掘りすることになるとは思ってなかったのですが、個人的にも面白かったので満足です。
以下、最後に少しだけ雑談です。
この話で個人的に面白く、結構大事だなと思っているのは、図2も樹形図としては全く誤っていない、というところです。
誤っているのは図2から“安直に”確率を求めようとしたところ一点のみであり、他の部分には問題はない(はず)です。
樹形図はあくまでもパターンを列挙するための、場合の数の単元における道具でしかなく、図2のような樹形図を考えるのはそれ自体間違いではありません。
逆に、図1の樹形図が考慮している項目が少ないために劣っているとも言えません。これはそういう樹形図である、だけなのですから。
しかし、より多くのパターンについて述べられている方が優れているような気がする気持ちもよくわかります。そこから求めた確率の方がより正確に感じるのも。
ニクいのは図2から求めた確率が各々1/2と、直感的な認識に一致しているところですね。モンティ・ホール問題は当時、数学者ですら間違えた(意見が分かれた)という話があるのも、むべなるかなといったところです。
因みに、友人はまだ納得してくれていません。
