
92. Relational Theory 振り返り
はじめに
今回は、リレーショナルデータベースの利用者なら誰でも知っているはずの Relational Theory について、そして Relational Theory と言えば、Normalization(正規化)、これらを復習することにします。
”利用者”という言葉をあえて使いました。
~ え?データベースを使ったシステムの開発者だけ知ってればよいのでは? ~
いえいえ、そのシステムを利用するユーザーも理解していないと、データベースに蓄積されたデータを効率的に取り出すことはできないので、知っていいて損はありません。
また、言うまでもないですが、Relational Theory、Normalization の知識がなければ、Entity Framework の言うところのデータモデルを定義することは不可能です。
今回はなるべく、技術屋以外の一般人にも理解できるぐらい平易な説明を行いつつ、”Art of Conceptual Modeling”で解説している概念情報モデルとの関連についても、当然ながら(私が書くのでw)言及することにします。
Relational Theory とは
Relational Theory、日本語で関係理論と言います。
Relation を基礎としたデータを扱う数学理論、それが Relational Theory です。Relation も Relational も Relationship も日本語に訳すと”関係”という感じになってしまうので、ニュアンスを保つため、英語表記もしくはカタカナ表記で、私はいつも書くことにしてます。
Relation
まず、大本の Relation ですが、

図の様な、カラムの組と、その値が確定している行群のことです。カラムのことを Attribute(属性)と呼びます。組の名前と各行の項目は明確に分けた方が説明がしやすいので、組の名前を”Attribute”、各行の”Attribute”に対応する値のことを、以下、”セル”と呼ぶことにします。
皆さんもよく、Excel で表を作りますよね。その際、ほとんどの表は、一番上がそのカラムのタイトルで、その下にそのタイトルの値を記した行が続くような形式をとりますよね。そのような表のうち、行の並びに意味がない、言い換えれば、行の順番を変えても支障がない表が Relation です。ちなみに、カラム(Attribute)の並びにも意味はありません。
上の表で、ProductId の値が上から下に行くにしたがって1づつ増えていて行の順番に意味があるように見えますが、Price の高い順から並べても構わないということです。
考え方としては、この表のデータを活用する目的に応じて、ProductId 順や Price 順、はたまた、Name のアルファベット順に並べ替えた表を作ればよい、ということです。リレーショナルデータベースでは、こういう表のことを View と呼びます。
なんだかんだ言っても、個々の Excel の表はある順番で書かれているんじゃないの、と思う方もいるかもしれないですが、それはその時々の単なる見栄え、偶々そうなっているだけで順番に意味はない、と考えるのが、本質を考えるということ。数学的思考を行う場合には、こういう割切りの考え方が重要です。
で、ここからが少々話がめんどくさくなってきます。単に Attribute の組とそれに従った行群というだけでは、データ群を効率よく保持することができません。ここで”効率よく”という言葉出てきましたが、
データ全体を必要最小限の領域量で保持できる
あるセルから別のセルに最短でたどれる
あるセルの値が変更されたとき、最小の手順で表全体の更新ができる
新規に行を追加する時、最小の手順で表全体の更新ができる
ある行が削除されたとき、最小の手順で表全体の更新ができる
という意味です。
そのため、Relation を前提に、Normalization、日本語では正規化というルールが加わります。
以下、めんどくさいので、Wikipedia から定義を引用して、その後に独自目線(テレ朝の朝のニュースバラエティでよくこの言葉を使って、「独自目線でお伝えします」っていうけど、あれ嫌いなんだよね…)の解説を加えることにします。
大抵の人は、身近に表があると思うので、その表が Relational Theory を満たしているかどうか、頭に描きながら読んでいってみてください。
第一正規化
関係がスカラ値のみを持ちうるとき、その関係を第1正規形 (first normal form; 1NF) であるという。スカラ値とはそれ以上分割できない値のことをいい、単一の数値や単語は一般にスカラ値だが、表や配列、カンマで区切った文字列などはふつうスカラ値ではない。第1正規形を満たさない関係は、その中の値を必ずしもリレーショナル演算(関係代数ないし関係論理による演算)の対象とすることができないという問題を持つ。
いきなりぶちかましてきましたね。数学に苦手意識がある人は、既にここで読むのをやめるかもしれませんね。
まず、スカラ値ですが、1、2、3、や 3.14 といった数字や、Curry や ShandyGaff とかひとまとまりの一つの意味を持つ文字列(”Oolong Tea”は一見すると二つの言葉からなっているように見えますが、”Oolong”だけだと”うすばか”、”Tea”だけだと”茶”で二つで漸く”烏龍茶”になるので一つの言葉と考えてよいです)、あるいは、味の良しあしを、”とてもうまい”、”うまい”、”どちらでもない”、”まずい”、”とてもまずい”という5段階だけで表現するような場合が、それに相当します。
※ 厳密に言うと、”スカラ値”とは自然数や実数等、順序が定まっていて、演算が可能な値のことを言うのですが、ここでは、気にしなくて構いません。
数字にしろ、文字列にしろ、一つのセルに二つの数字、あるいは、二つの独立した意味を持つ文字列が、”," で区切られて保持されているようなものはダメです。
ただし、経験上、例えば、モノの3次元空間上の位置や速度、加速度、地球上の緯度経度などは、一見すると、3つの数字(緯度経度は二つ)からなりますが、一つのセルに入れても構いません。
要するに、全てのセルの値は、そういう、その値がさす現実世界の対象がただ一つになっているように表を作りなさい、ということです。
Excel の表では、左側のカラムの値に対して、右側のカラム群が複数の行で繰り返されるような表をよく見かけるし、私自身も良く作りますが、このような表は第一正規化された表ではないことになります。
第二正規化
ある関係が、第1正規形で、かつ、すべての非キー属性が、すべての候補キーに対して完全従属するとき、第2正規形 (second normal form; 2NF) であるという。つまり、第2正規形では、候補キーの一部に関数従属する非キー属性があってはならない。
あ~、もうダメ…という悲鳴が聞こえてきそうな定義です。順番に説明していきます。
まず、”非キー属性”、”非”がついているので、まずは、”キー属性”を説明しないといけないですね。あ、ちなみに、”属性”とは、”Attribute”の日本語訳です。
キー属性とは、Relation の表を構成する全ての行で重複しない値を持つ Attribute のことです。前に挙げた図の例で言うと、ProductId がそれにあたります。表で見ての通り、1から始まる整数で全て異なる値をこの Attribute のセルに入れなければなりません。非キー属性とは、キー属性じゃない方なので、ある Attribute に対応する行のセルが同じ値であっても構わないということです。勘の良い読者は、”Name” もキー属性なんじゃないのと思うかもしれません。正解の場合もあり不正解の場合もあります。正解の場合、複数のキー属性が一つの行に存在することが問題になりそうですが、以下説明していく制約を満たすなら、Relation に複数のキー属性があっても構いません。
※ ”Name”がキー属性の場合、”Name”に対応する全てのセルは別の文字列でなければならず、かつ、”ProductId” の値と1:1対応していなければなりません。そのような場合、便宜上、ProductId のことを第1キー属性、Name のことを第2キー属性と呼んだりします。
※ ”Name”が非キー属性の場合、”Name”に対応するセルに同じ文字列が保持されていても良いことになります。例えば、図に示した表がスーパーなどの売り場で、同一名の商品を複数の会社が製造して納品しているような場合は、同じ値の”Name”の行が複数あっても構わないでしょう。住所録や住民台帳で、同姓同名の人物に相当する行が複数存在するのと似た状態です。
また、キー属性は二つ以上の Attribute の組み合わせになる場合もあります。この場合、一つの Attribute がただ一つのキー属性である場合も含め、キー属性を構成する Attribute 群のことをまとめて、”候補キー”と呼びます。
次に、”完全従属”という言葉です。まず、”完全従属”のもとになる”関係従属”について説明します。図に書いた表では、キー属性の ”ProductId”の値、例えば、”3”を選ぶと、その行の、”ShandyGaff”、”Cocktail”、”900”がすべて決まることを意味します。逆に、”Price”の値、例えば、”500” を選んだ場合、”500”のセルは複数あるので、他の Attribute の値をただ一つに決めることはできないので、従属していないことになります。この様な”関数従属”がない(言い換えると候補キーでない、あるいは、候補キーを構成しない) Attribute のことを”非キー属性”と呼びます。
候補キー、これは、”決定項”とも呼んだりしますが、候補キーが複数の Attribute から構成される場合、非キー属性のどれかが、候補キーを構成する Attribute 群全体でなく一部分だけの Attibute 群に関数従属している場合、それを”部分従属”と呼び、”部分従属”する非キー属性が一つもない、つまり、候補キー全体に対してだけ、非キー属性群が関数従属する場合、”完全従属”するといいます。
え?「何言ってるかわからない」ですって?…まぁそうでしょうね。
前に挙げた図だとよく判らないので、若干修正しますね。

この Relation は、便宜的に {ProductId, Name, CategoryName} の3つの Attribute で候補キーとしました。非キー属性の Price はこの候補キーに完全従属していますが、”Category Description”は、その名前からして、”CategoryName”にしか従属していませんね。そんなわけで、この Relation は第二正規化のルールを満たしていないことになります。なので、Relational Theory 的に NG になるわけです。
「おい、ちょっとまて。そもそも ”Category Description”のセルがスカラ値じゃなくね?」はいはい、見ての通り、文章になっていますが、CategoryName の項目名を説明する一つの意味の塊ということで、特に問題ないという理解でお願いします。
このテーブルを第二正規化のルールを満たす表に変更すると、

Category Name に従属する部分を独立した Relation に分割しました。その結果、Categories に CategoryId というキー属性(候補キー)を追加し、Products 側で、その値を使ってセルの値を埋める、CategoryId という Attribute が加わりました。この様な外部の Relation のキー属性を参照する Attribute のことを、”外部キー”と呼びます。Products 側は、CategoryName が CategoryId になったものの、引き続き、3つの Attribute 群で一つの候補キーにしています。
第二正規化された Relation 群には以下のメリットがあります。
Product がない Category の情報をあらかじめ保持できる
Category Description を変更したいとき、Categories のセルを一つだけ変更するだけで作業が完了する。Category Name も同様。
このあたりまで来ると、Excel で作成する表とは趣がだいぶ違うな、という感覚になってくるでしょう。
第三正規化
ある関係が、第2正規形で、かつ、非キー属性があるならば、それら全てが候補キーに非推移的に関数従属するとき、第3正規形 (third normal form; 3NF) であるという。
この説明も、”非推移的”という言葉が判り難いですね。”推移的に関数従属する”を説明すると、まさに、図2で紹介した Relation が”推移的”な属性関係が存在する例になっています。図2では、3つの Attribute の組で候補キーになっていますが、とりあえず、ここでは、ProductId という Attribute が一個だけで候補キーになると考えてください。この Relation では、ProductId(Aとする) が決まると CategoryName(Bとする)が決まり、Category Description(Cとする)は CategoryName が決まるという、A→B、でかつ、B→C という関数従属があります。このような二段階の従属が、一つの Relation にある場合に、推移的に関数従属する”といいます。
”非推移的”はその反対で、そのような”推移的な関数従属”にあるような非キー属性はないということです。ということで、図3は、そんな推移的な関数従属は無いので、第二正規化で、かつ、第三正規化された Relation であると言えます。
今現在、デファクトで利用されている Relational Database は、第三正規化までしか対応していません。ベンダーが Relational Database の実装を考えたとき、実用上それで充分という判断だったようです。
しかし、数学的な Normalization(正規化)はより高次な正規化がまだまだ続きます。
ボイス・コッド正規化
ある関係上に存在する自明でない全ての関数従属性の決定項が候補キーであるとき、かつそのときに限り、その関係はボイス・コッド正規形 (Boyce/Codd normal form; BCNF) であるという。すなわち、ボイス・コッド正規形では、すべての属性が候補キーに完全従属する。
何故、第N正規化じゃないんだろう…私も知らない。
これ、例えば、

こういう Relation があったとします。”Famous Shop”というのは、”Name” の値、例えば、”Curry” なら、この店しかないよね的な店の名前で、かつ、その店、この場合なら”Kim”という店といえば、”Curry”だよねというような場合であるとします。そうすると、”ProductId” の値を一つ選択すれば、関数従属的に、”Famous Shop”が決まりますが、逆に”Famous Shop”の値を一つ選択すれば、”ProductId”も決まります。これ、”Famous Shop”も、実は候補キーだとしても数学的な定義的には問題がないことになります。ボイス・コッド正規化は、そういう関数従属はあっちゃだめよということなので、

にすると、ボイス・コッド正規化された Relation であるといえることになりますとさ。
第四正規化
第4正規形 (fourth normal form; 4NF) では候補キーではない属性への多値従属性をもった属性があってはならない。
はいはい、次は、”多値従属性”ですね。この用語の意味が判らないと、この正規化の意味は分かりませんね。
より簡単な説明が思いつかないので、Wikipedia の説明を拝借。
多値従属性の定義を述べる。 R を関係とし、A, B, C を、R の属性集合の任意の部分集合とする。 R のある (A値, C値) 対に対応するB値の集合がA値だけに依存し、C値には独立かつそのときに限り、B は A に多値従属しているといい、次のように表す。
A ↠ B
多値従属性がある Relation の例も思いつかないので、Wikipedia の例を拝借。

上の説明を、”A”⇒”コース”、B⇒”参考図書”、”C”⇒”講師”に置き換えて読んでみます。それでも判り難いのは変わらない(苦笑)。
そもそも図6の Relation は、候補キーが{”コース”,”参考図書”,”講師”}なので、”候補キーでない属性”が存在しません。どういうこと?
確かに、この3つの属性の組が候補キーなら、ボイス・コッド正規化は満たされていますね。色々と考えた末、この Relation に、”ID”という Attribute を追加して、”ID” の値は重複しないとすれば、一応の説明は成り立つのではないでしょうか。
”ID”をキー属性(候補キー)として、元々の3つの Attribute は候補キーではないとします。ある”コース”の値に対して”参考図書”の値が複数対応していて、かつ、”講師”の値も複数対応しています。つまり、
”コース”↠ ”参考図書”
”コース”↠ ”講師”
で、かつ、行ごとの”参考図書”と”講師”の対応は、特に無関係に見えるので独立しているので、多値従属している Attribute が存在することになり、第四正規化されてはいないことになりますと。
で、図6. の Relation の第四正規化の結果が、Wikipedia によれば、

になっていて、どちらの Relation にも ”ID”という Attribute を追加すれば、なんとなく理解できるかなという感じです。
この判り難さは、後の方で再度触れますが、数学的な定義を前面に押し出している(コースへの参考図書の割当てと講師の割当ては無関係だよっていう事実が後回しというか先に語られていない)こと、そして、他の正規化の定義にも言えることですが、否定文で定義されていることが、原因なのではないかと思います。
第五正規化
第5正規形 (fifth normal form; 5NF) を満たす関係は、その関係が第4正規形であり、さらにその関係に含まれる結合従属性の決定項が候補キーのみである場合、かつその場合だけである。 第5正規形は、射影-結合正規形 (project-join normal form; PJ/NF) とも呼ばれる。
さて、これが最後の高次正規化です。こちらもぱっと見、理解が難しいですね。”結合従属性”って何よ、という点ですね。
これについては、正規化理論における結合従属性を解説 | べんとのブログ (bentblog.net) に詳しいので、そちらを参考にしてください。
これだとちょっと乱暴なので、射影と結合についてだけ、簡単に説明しておきます。
射影
Relation から、特定の Attribute のセルだけ抜き出す。抜き出すのは一つ以上の任意の Attribute であり、全ての Attribute でも構わない
結合
二つの Relation で同じ名前(意味)の Attribute がある場合、それぞれの Relation のセルの値が同じ行を連結して一つの Relation を作る
第四正規化にしろ第五正規化にしろ、これらの規則を満たしていない Relation は、冗長性があるので、まだまだ分割できる可能性がありますよ、ということです。
分割すれば、行の追加・削除や、セルの値の変更にかかる手順が少なくなる可能性があり、データ修正時の間違いを減らせる可能性があることになります。一番ありそうなデータ不整合の発生は、あるセルの値を更新したとき、実は、同等の意味を持つ、あるいは、関数従属している別のセルの更新も必要なのに、それを忘れた、とか、ある Relation の一行について、その行のキー属性のセルに関数従属している別の Relation のセルがあるにもかかわらず、その一行だけを削除してしまった、とかでしょう。
逆から考えると、高次の正規化をすればするほど、データ入力時の制約条件が増えていくので、いい加減なデータの入力を排除できたり、そのデータベースを元にしたビジネスロジックのコードで書かなければならない制約処理が少なくなっていきます。
その後、第五正規化の判りやすい説明と例がないか調べたところ、
を見つけました。このページに記載の定義と説明を参考までに拝借します。
自明でない結合従属性∗(𝑅𝑆1,⋯,𝑅𝑆𝑛)が成り立つならば𝑅𝑆1,⋯,𝑅𝑆𝑛は常に𝑅𝑆の超キーであるという制約を第五正規形制約という。𝑅𝑆が第五正規形制約を満たすとき,𝑅𝑆は第五正規形であるという。
第五正規形(fifth normal form)は射影結合正規形(projection join normal form)とも呼ばれ,頭文字を取って5NFやPJNFと略されます。結合従属性が多値従属性の一般化であることを踏まえると,第五正規形は第四正規形制約を守りながら制約をより強くした正規形であることが分かります。第五正規形に明示的に変形する必要がある場合は,「違和感の覚えるリレーションスキーマではないが,無損失結合分解となるように複数のリレーションスキーマに分けてあげた方が更新不整合を起こす可能性が低くなりそうだ」といったようなリレーションスキーマであることがほとんどです。5NFを一言で表すならば「複数の表の結合として分解不可能な最小単位である」です。
紹介されている例も掲載しておきます。

スキーマの定義
以上、Relational Theory のもとになる Relation と Relational Theory を満たすための Normalization(正規化)について紹介してきました。Relational Database を使う場合は、これらのルールを元に複数の Relation の構造を決めていくことになります。複数の Relation の構造のことを”スキーマ”と呼び、この構造を決めていく作業のことを、”スキーマの定義”と言います。
Relation は、一般的なリレーショナルデータベースでは、”テーブル”と呼ぶので、以下、”テーブル”という言葉が出てきたら、”Relation”のことだと思って読み進めてください。
スキーマについては、忘れらない経験があります。90年代中ごろ、数十人規模で使っていたリレーショナルデータベースを使った IT システムに蓄積された情報を分析したくて、IT システムの開発担当者に「スキーマを教えてください」と頼んだことがあります。担当者の答えは、「スキーマって何ですか?」でした。よくよく聞いてみると、その担当者には Relational Theory に関する知識は皆無で、巨大な一枚のテーブルに全てのデータを蓄積するような作りになっていることが判明しました。いやぁ。。。びっくりしたよ。
それが判った時点で、その当時複数の開発チーム間で生じていた軋轢の8割がたが、このくそなリレーショナルデータベースのせいで生じていると腑に落ちました。その後の複数の経験も加味すると、世の中で大々的に使われているリレーショナルデータベースを使った IT システムの多くが、Relational Theory を知らない素人技術者が開発しているのではないか、そして、実はそれが根本原因で様々なシステム障害が発生しているのではないかという疑惑が払しょくできないでいます。今時は、NoSQL なデータベースも多くありますが、その場合でもデータ設計においては第三正規化ぐらいまでは理解して活用できるレベルでないと出来上がるシステムはくそなのは間違いありません。
もし、データベースを使ったシステムを開発している人に出会ったら、「スキーマって知ってます?」と聞いてみてください。「知らない」と答えたら、そのシステムの利用はやめましょう。
スキーマは、以下の項目で定義が行われます。
Relation(テーブル)の定義
Relation を構成する Attribute 群
各 Attribute の名前とデータ型、及び、制約
図3で説明したように、二つの Relation(テーブル)が定義されていて、片方の Relation の主キー Attribute(複数の組でも可)が、別方の Relation で外部キーとして参照されるので、Attribute の制約は、
主キー Attributeかどうか
外部キー Attribute かどうか
外部キー Attribute なら、どの Relation の 主キー Attribute を指すのかに関する情報
で記述されます。これがスキーマ定義のミニマムセットです。
定義は、SQL の DDL(Data Definition Language)で厳密(実際の Relational Database システムが実行できるレベル)に記述されたり、ER図と補足の文で記述されたりします。
SQL
SQL は、Structured Query Language の頭文字から名付けられた Relational Theory に基づいてリレーショナルデータベースを操作するためのスクリプト言語です。SQL は、Relational Theory を考え出した、”エドワード・F・コッド”が考案したスクリプト言語です。1986年以降は、ANSI、のちに ISO で標準化がなされています。その国際標準に準拠した形で、例えばマイクロソフトなら T-SQL といった、ベンダー各社の若干の方言が加味された SQL 言語が実際に使われています。SQL は提案された当初から、Relational Theory を完全に対応できていないという批判はあるものの、実用レベルで駆使されています。
SQL で記述できることは大体以下の通りです。
スキーマの定義
スキーマに従った行の追加・削除、セルの値更新
スキーマに従ったデータのクエリ
あるテーブルの射影
テーブル間の結合
セルに対する論理・算術演算
他にも View の定義とか諸々ありますが、このぐらい知っていれば実用上問題ないでしょう。
SQL を考案したコッドさんは、ソフトウェア技術者の様な専門職ではなく、一般ユーザーが使えるスクリプト言語を定義することを目指していたようです。当時は、コンピューターがどう動くかという知識がないとプログラムは書けなかったのですが、SQL は Relational Theory だけ知っていれば、その知識に基づいて、コンピュータの内部知識がなくても、所望のスキーマが定義でき、データの更新・検索ができるように SQL を定義したとのことです。しかし、ここまで読んできたデータベース初心者なら痛感すると思いますが、そこそこのプログラムを書くのに必要な知識の理解より、Relational Theory を理解することの方が何倍も難しいという皮肉な事実があって、コッドさんの意図通りにはいっていないのは明らかでしょう。
ここまで高次正規化についてメリットだけを意図的に挙げていたのですが、そして、それは数学的な Relational Theory の本質的な問題ではないと私は考えていますが、SQL 文を書こうとすると、そのデメリットが目立つように感じています。高次正規化に基づいて分割されたテーブル群は、データの更新の際は特に問題ないのですが、クエリ(データの検索)文を書こうとすると、途端に、何段にもわたる結合(結合は一種類じゃないし)の記述、複雑(?まぁデータモデルの対象世界が複雑だからしょうがないんだけど)なスキーマの理解等、記述の苦しみが生じてしまいます。これが嫌で、腑抜けたスキーマを定義してしまう技術者もいるのかもしれませんね。
また、個人的には、データベースベンダーの実装の問題だと思ってはいるのですが、実際のデータベースシステムを使った場合、使用するコンピュータの性能も相まって、何段にもわたる結合の SQL スクリプトを実行しようとすると、当然実行パフォーマンスの問題も生じてきます。リレーショナルデータベースは、複数の利用者が同時にアクセスするので排他処理やトランザクション処理も必要です。
ただ、それらは使っているハードウェアの問題が大きいので、今時のクラウド時代、もちろん、サービス利用コストが、高性能はハードウェアを使ったことにより防げる損失コストと生み出される利益を食いつぶさない範囲であることは必須なのですが、より品質・性能の高いデータベースサービスを使って、本来の Relational Theory に従ったスキーマを定義した方が、私は良いと考えています。いい加減なスキーマ定義の場合、その手を抜いた代償は、ビジネスロジックを含むアプリケーション側が負担することになります。スキーマで現実世界のデータの制約が定義されているなら、その制約を破るデータ更新はリレーショナルデータベースシステムが弾いてくれますが、いい加減なスキーマ定義の場合は、それらの制約はビジネスロジックやアプリケーションのプログラムコードで実装しなければなりません。そして、その場合は、Relational Theory の様な数学的基盤が無いので、そのプログラムコードが妥当かどうかの判断は非常に難しいものになります。
その実装コスト、テスト、運用・保守にかかるコストを考えたら、ちゃんとしたスキーマ定義を行う方が、楽。スキーマ定義で苦労するか、後々のロジック実装、テスト、運用・保守で苦労するかのどちらがいい?って話。
概念モデリングからの考察
さて、Relational Theory、及び、それをベースにした SQL について紹介を行いました。個人的見解ですが、Relational Theory はデータモデリングの基盤として実用上十分ではあるものの、いくつか欠陥があると思っています。
Relational Theory の欠陥
一つ目は、Relational Theory はあくまでも数学理論にすぎないという点です。コッドさんが Relational Theory を提案する際、現実世界にあふれる様々なデータを扱うためのモデルが必要だという動機が含まれているのはもちろん間違いはないでしょう。しかし、では、
Relation(テーブル)とは現実世界の何に対応しているのか
Attribute(属性)とは現実世界の何に対応しているのか
Relation の行は現実世界の何に対応しているのか
が Relational Theory で明確に定義されているかというとそうでもありません。実際のところ、現実世界のデータ群を数学的な Relation と正規化の定義に従ってスキーマを定義すれば、冗長性がなく一貫性が保ちやすいデータモデルが出来上がるというだけのことです。そして、現実世界とモデルとの関係をきちんと定義するには、11. ”世界は存在しない”が”意味の場”は多数存在する ~ 概念モデリング基礎付けの最後のピースを埋める|Knowledge & Experience (note.com) で考察したように、存在とは何か、認識とは何かという哲学的な見解や解釈が必要であり、Relational Theory がその領域についてきちんとした見解や解釈があるようには見えません。これまで何人かの物好きが、それぞれの見解を後付けしているかもしれませんが。
そういう意味においては、Relational Theory における Relation はただの数字や文字列がちりばめられた表にすぎません。Relation 間の Relationship についても、単に、Relation の行から別の Relation への数学演算の写像が存在するにすぎず、それが現実世界の何に対応しているかについての見解や解釈は存在しません。
このことは、Relational Theory に従って定義・記述されたデータモデルが、モデル化対象の現実世界に対して妥当かどうかの判断基準がないことを意味します。
二つ目は、Relational Theory が、数学の”集合論”を基礎としている点です。ラッセルの有名なパラドックスで明らかなように、素朴な集合論は数学的な矛盾を内包しています。であるならば、Relational Theory もそれに起因する何らかの矛盾を内包している可能性は否定できないでしょう。
ただし、この問題は、5. 概念モデリングに関する圏論的考察 ‐ 議論のとっかかりとして|Knowledge & Experience (note.com) で紹介している、数学の一分野の”圏論(Category Theory)によって、矛盾を内包しない、注意深い集合論の基礎付けがなされていたり、Relational Theory のスキーマを圏論で解釈するスキーマ圏も提案されているので、既に解決済、あるいは、近いうちに解決される問題だと思われます。
三つめは、一つ目の問題点にも関連するのですが、データモデルを定義・記述する際に使う、語彙の問題です。データベースの Relation(テーブル)を定義する際、その Relation には名前を付けます。また、Relation を構成する Attribute も名前を付与します。Attribute の値のデータ型もまた然り。
8. 概念モデルの言語論理学からの考察 ~ Frege、Russel、Wittgenstein|Knowledge & Experience (note.com) で紹介した、ウィットゲンシュタインの言語哲学によれば、語彙の意味は、その語彙が属する言語空間全体との関連において決定されます。また、スキーマで定義された Relation 群と Relation 間の Relationship によって、データベースに保持されたデータ群から述語文を構成することができ、その述語文が現実世界に存在するならば、真であるということになります。Relational Theory は暗黙的にですが、この考え方は採用しているようです。ただし、何が真なのかは、3. モデリングとは ~ 現象学からの考察|Knowledge & Experience (note.com) でも紹介している通り、スキーマ作成者と、そのスキーマ作成に関係するステークホルダー達全員との合意を得るのはなかなかにタフな作業になるでしょう。
Relational Theory にしろ、ウィットゲンシュタインにしろ、使用する語彙が属する言語空間は、ただ一つであることを前提にしているように思えます。しかし、11. ”世界は存在しない”が”意味の場”は多数存在する ~ 概念モデリング基礎付けの最後のピースを埋める|Knowledge & Experience (note.com) で紹介した新実存主義によれば、ただ一つの世界は存在せず、認識する側にとってのそれぞれの”意味の場”が多数、同時並行的に存在する、そして、私としては非常に腑に落ちる言説であるので、そのままその通りだと思っている言説からすると、モデル化対象の”意味の場”が異なれば、同じ対象を見ていても、まったく異なるデータモデルが出来上がってしまいます。Relational Theory に限らずデータモデリング系は、何をモデル化対象としているかを明確に示すことが必須であるといってよいでしょう。
概念モデリングからの回答
概念モデリングについては、”Art of Conceptual Modeling”の一連のドキュメントをご参照いただくとして、上に挙げた欠陥に対する概念モデリングからの見解を述べようと思います。
その前に、Relational Theory の用語と概念モデリングの用語の対応付けを示しておきます。
Relation ⇔ 概念クラス(Conceptual Class)
Attribute ⇔ 特徴値(Property)
データ型 ⇔ データ型
行(Record)⇔ 概念インスタンス(Conceptual Instance)
正規化 ⇔ 結果として従う
Relationship ⇔ Relationship
概念クラス間の二項 Relationship はそのまま該当
関連クラス付きの Relationship は、二項の概念クラスを A と B、関連クラスを R とすると、A、B、R の3つの Relation と A ↔ R、及び、R ↔ B の Relationship とほぼ同等
概念情報モデルの Super-Sub Relationship に相当する Relational Theory の正規化はない(多分)
スキーマ ⇔ 概念情報モデル(Conceptual Information Model)
Relational Theory には該当する概念無し ⇔ 意味の場(ドメイン)
さて、欠陥の一つ目は置いておいて、まず、二つ目の欠陥についての考察を述べることにします。概念モデリングでは、未だ、数学的に厳密な定義は済んではいませんが、数学の圏論をベースに、モデリングの道具立てを全て定義できる見通しを立てています。
永年、概念モデリングのベースになっている Shlaer-Mellor 法に取り組む多くの学習者の姿を見続けてきましたが、概念クラスと Relationship の世界(スキーマの世界)と概念インスタンスの世界(レコードの世界)の区別を習得するのが一番難しいようです。
Relational Database においても、もしかするとスキーマの世界とレコードの世界の区別が曖昧なままデータベース設計に取り組んでいる技術者が多いのかもしれません。
5. 概念モデリングに関する圏論的考察 ‐ 議論のとっかかりとして|Knowledge & Experience (note.com)
で書いている通り、概念インスタンスの世界(圏I)と概念情報モデルの世界(圏C)を明確に圏論の枠組みを使って定義しています。更に、1つ目と三つ目の欠陥にも絡みますが、モデル化の対象世界を圏W(正しくは圏Sだろう)についても言及し、モデル化対象世界とモデル上の概念との対応付けを行っています。
細かいところでちょっとした差異はあるようにも思えますが、Relational Theory のスキーマ圏と概念モデリングの概念情報モデルの圏C はほぼ自然同値だと思われます。
というわけで、概念モデリングは、数学的には圏論を基礎づけの理論として採用しています。
さて、1つ目ですが、内容的には3つ目も絡む話なので、まとめて回答します。
まず、モデル化対象世界との対応付けは、
7. 現実世界のダイナミクスと概念振舞モデルに関する考察|Knowledge & Experience (note.com)
に詳しく書いてあるのでご一読いただくとして、一通りここに書いておきます。
モデル化の対象
新実存主義の”意味の場(Sense of Field)”。”領野”と訳される場合もある
Shlaer-Mellor 法の時代から、ドメインという概念があり、この用語の定義は、まさに新実存主義で提唱された”意味の場”と同等
”意味の場”において、それぞれ区別可能な値を持つ何か ⇒ 概念インスタンスの値を持った特徴値
”意味の場”において、それぞれの特徴値の取り得る値域 ⇒ データ型
”意味の場”において、複数の値で特徴が記述される、それぞれ区別可能な何か ⇒ 概念インスタンス
ビルや部屋、商品、人等、形のある目に見えるものだけでなく、契約や注文、役割等、具体的な形がなく目にみえなくても論理的に存在し区別可能なものも”区別可能な何か”に相当する
2つのそれぞれ区別可能な何かの間に、”意味の場”において存在する意味的なつながり ⇒ リンク
”意味の場”において、同じ分類として認識できて、かつ、共通の特徴値の組を持つ概念インスタンスの分類 ⇒ 概念クラス
共通の組を構成する特徴値 ⇒ 概念クラスの特徴値
特徴値には、概念クラスをひな型にして存在する概念インスタンスそれぞれを識別するための識別子の値を保持する、一つ、あるいは、複数の特徴値が必ず存在する
”意味の場”における、概念インスタンスのリンクの分類 ⇒ Relationship
概念クラスの片方から相手方を見たときの意味と概念インスタンスの多重度({必ず1つ|無いか、あっても1つ|1つ以上の複数、無いか、複数}の4つのうちのどれか)を必ず定義する。別の方向についても、意味と多重度を必ず定義する
二つの概念インスタンスの間に Relationship をひな型にリンクがあることを示す値を保持する、一つ、あるいは、複数の特徴値をどちらか一方の概念クラスに必ず存在する
関連クラスや Super-Sub Relationship 等、一部省略していますが、こんな対応付けになっています。この様に、Relational Theory の欠陥として指摘した一つ目と三つ目に対して、明確な定義が与えられていることがご理解いただけるでしょう。
概念情報モデルにおける正規化
前述の意味の場に存在する概念群と概念モデルの要素の対応付けを元に、Relational Theory の Relation、Normalization(正規化)を再検討してみることにします。
まず、Relation ですが、一つ前のセクションの対応付けから、Relational Theory における Relation の定義と形式的に同義であることは明らかです。
第一正規化についても、概念クラスの定義から、そのまま満たすのは明らかです。
第二以上の正規化については、書籍や Wikipedia をはじめとする様々な解説で正規化の例として挙げられている表群を見ると、正規化によって分割されてできた表それぞれが、概念モデリングの概念クラスに相当する”意味の場”における存在の分類として考えられる表になっています。
感覚的でざっくりとした意見で申し訳ないですが、一つ前のセクションの対応付けに従って作られた概念情報モデルは、第五正規化までを含む、適切な正規化が自然にできあがると考えられます。
Relational Theory におけるボイス・コッド正規化以上の高次の正規化それぞれの解説に、「その分割をするかどうかは状況による」といった意味の但し書きが書かれていますが、妥当かどうかの判断は、結局のところ、概念モデリングが前提としているモデル化対象の現実世界(意味の場)との対応付けを元にした検討になるのは間違いありません。
概念モデリングの Super-Sub Relationship はちょっと違う
まずは、概念モデリング Super-Sub Relationship とは何かから話を始めます。”物理現象の値を計測するデバイス”という意味の場における、”センサー”を考えてみます。センサーには温度を測ったり、気圧を測ったり、湿度を測ったりと様々なセンサーが存在します。これを Super-Sub Relationship を使って概念情報モデルで書くと、

こんな風に、白抜きの△の頂点が Super 側の概念クラスに接して、△の底辺の同じ位置と、Sub 側の概念クラス群とを結ぶ線で、Super-Sub Relationship を表現した図になります。
オブジェクト指向に慣れた読者には「あ~、継承ね」とすぐに思ってしまう方がいるかもしれませんね。しかし、違います。勘違いしないでくださいね。
Super-Sub Relationship の定義は以下の通りです。
Sub 側の概念クラスをひな型とする概念インスタンスが一つ存在する場合、それに対応する Super 側の概念クラスをひな型とする概念インスタンスが必ず1つ存在する
Super 側の概念クラスをひな型とする概念インスタンスが一つ存在する場合、Sub 側の概念クラスの一つをひな型とする概念インスタンスが必ず1つ存在する
Super-Sub Relationship の Sub 側の概念クラス群は、Super 側の概念クラスに対して、モデル化対象の意味の場において、同じ範疇の意味で関連付けられていなければならない
Super側、Sub 側に関係なく、概念クラスの特徴値を参照する場合、その特徴値の名前は、概念クラスにおいてのみ意味を成す。
オブジェクト指向プログラミングにおける”継承(inheritance)”は、継承される class が抽象クラスではない場合、継承する sub class が無くても instance 化できるので、1番目の定義に反します。更に、ある class に対してプログラマが継承する sub class を記述する時、既に他で定義された class 群と意味的に無関係な sub class を定義可能なので、3番目の定義にも合致していません。4番目の定義は、ちょっと難しく書いてしまいました。オブジェクト指向プログラミングの場合、継承すると、親 class に定義されたメンバ変数が public、あるいは、protected の場合、子 class の instance は、その名前を自分のスコープで参照できるようになっていますが、概念モデリングでは、概念クラスの特徴値は、概念インスタンスにおいては、それぞれの概念インスタスの特徴値としてしか参照できないとされており、Sub 側の概念インスタンスは、自分がひな型となっている概念クラスの特徴値群しか持っておらず、Super 側の概念インスタンスは単に Super-Sub Relationship でつながった概念インスタンスにすぎないので、自分の特徴値ではなく、参照できないということです。
※ くどく書いているのは、「あ~ Super 側の概念クラスは抽象クラスで、その特徴値は private なのね」という誤解を防ぐためですので、悪しからず。
概念情報モデルを図示化する時は、UML 表記を使うので、オブジェクト指向プログラミングに詳しい人は、どうしてもそちらに引っ張られてしまうかもしれませんが、違うよということです。
概念情報モデルの Super-Sub Relationship を見るときには、一旦、オブジェクト指向プログラミングのことは忘れてくださいね、と言った方が良いかもしれませんね。
さて、この定義を元に、Relational Theory の Relation 群を構成すると、例えば、

こんな風になりますが、前に挙げた Super-Sub Relationship の定義の1~3 を正しく規定する高次正規化はありません(マイナーな高次正規化はいろんな人が提唱しているのでその中にはあるかも)。
さて、前に挙げた定義の中で、2番目と3番目に着目してみることにします。これ、実はすごく厳しい制約なんですね。モデル化対象の意味の場を正確に写し取るのが概念情報モデルの役割なので、Super-Sub Relationship で記述した場合、Super 側の概念クラスに Sub 側で列挙された概念クラス群しか、その意味の場には存在しませんよ、という宣言を意味します。図SS1. でいえば、
センサー(S)は、温度センサー(T)と圧力センサー(P)、湿度センサー(H)しかないぞよ!
ということを宣言したモデルであるということです。「え?加速度センサーとか、ジャイロとか光センサーとかいっぱいあるじゃん世の中には!」もしモデル作成者がそう思っているなら、図SS1. の概念情報モデルは正しいモデルではない、ということです。Super-Sub Relationship を使う場合には注意が必要です。
オブジェクト指向プログラミングの黎明期から見てきましたが、何故か、この△の矢印を見ると、使いたがる人が多い気がします。オブジェクト指向プログラミングの継承しかり、Shlaer-Mellor 法の Super-Sub Relationship しかり、Azure Digital Twins の DTDL の extends しかり。
オブジェクト指向プログラミング黎明期に出版された書籍の中には、継承?を使った動物の分類図の様な珍妙な例を挙げて、これが”オブジェクト指向だ!”的な説明をしていたものもありました。当時の読者の中には、「それで何の意味があるの?」と疑問に感じた人も多くいたに違いありません。
何故なんでしょうね?
概念モデリングに限って言えば、このセクションで解説した通り、Super-Sub Relationship は非常に厳しい制約を課すものであり、安易に使うと、作成したモデルをリリースした後、Sub 側の概念クラスに相当するものを見つけるたびに、概念情報モデルの書き換えが発生します。リレーショナルデータベースに例えていえば、その都度データベースのスキーマ変更が発生するということを意味します。これ大変だよ。
ぱっと見、Super-Sub Relationship だと思えるものの大半は、概念クラス間の2項 Relationship で記述可能です。
今回取り上げた図SS1. のセンサーの例では、概念モデリング ~ 虎の巻|Knowledge & Experience (note.com) で説明している”仕様パターン”を使って、二項 Relationship に書き換えることができ、そうすれば、よほど変わったセンサーが出てこない限り、概念情報モデルの書き換えは生じず、概念情報モデルで定義されたスキーマに従って、概念インスタンスとリンクを増やすだけで済むことになります。概念モデリングを行っているときは、安易に Super-Sub Relationship は使わず、脳みそ搾り上げて十分に吟味してからモデルを作成しましょう。
そういえば、Relational Theory には、Super-Sub Relationship や継承にあたる正規化が無いと解説しましたが、”無くても実用上問題ないやん”という判断なのでしょうかね。いっそ清々しい(苦笑)。
ちなみに、オブジェクト指向プログラミングにおいては、△の矢印は、継承(線は実線で表される)だけでなく、”realize”、または、”implements” という意味を持つ(線は点線で表される)ものもあり、現代的なプログラミングではこちらを活用する方が一般的でしょう。いわゆる、interface と呼ばれるものですね。interface には仮想関数(C#は property も)だけ定義し、その inteface を使う側(アプリケーション側と呼ぶことにします)は、そのシグネチャだけを念頭にプログラムコードを書き、interface を realize、あるいは、implrements する側の class では、それぞれの仮想関数(C# の場合は property のアクセッサ)の実装をプログラムコードとして記述します。こうすることにより、プログラムコードをビルドしたバイナリモジュールの差替えが可能になり、実装技術の変更への対応時、アプリケーション側は一切影響を受けないようなシステム構成が可能になるという素敵な考え方です。
これ、概念モデリングの”意味の場”的にみると、アプリケーション側の”意味の場”と、実装側の”意味の場”は異なり、それを、プログラミング言語仕様という”意味の場”で二つの”意味の場”の記述を対応付けている、という風に解釈が可能なんですね。合理的だ。
オブジェクト指向プログラミング黎明期(1990年代)では、なんだか知らないですけど、継承がもてはやされていましたが、30年の時を経て、いろんな理由で、継承はかえって再利用性を低くするという認識が一般的になって、重要なのは、”realize”、あるいは、”implements”を使う、”interface” だよね、というのが現代の感覚。今では当たり前になった、コンポーネント指向(英語だと Component Based なので、邦訳はちょっと微妙)も、この原理に基づいています。インターネット上の複数のサービスが連携してシステムを構成するサービス指向も、また然りです。
だからと言って、interface を間違って多用するのもまたNG。私は過去、1つの interface を実装する20個以上の class の定義が name というメンバー変数の値だけ違うというコードを見たことがあります。「それさ、class を一個だけ定義して、使う時に name のメンバー変数の値を確定させりゃいいじゃん 」ってことです。オブジェクト指向プログラミングの何たるかの理解が根本的に間違っていたという訳。
いずれにせよ、はさみと道具は使いよう、どうせ使うなら正しく使うのがベストってことですね。
概念モデリングは Relational Theory のスキーマ定義として活用できる
これまでの考察から、概念モデリングで作成した概念情報モデルは、Relational Theory のスキーマ定義として活用できるのは明らかです。
具体的な方法は、
ビジネスシナリオを元に作成した概念モデルを Azure Digital Twins、Azure Functions を使って実装する|Knowledge & Experience (note.com)
に詳しいので読んでみてください。数学的な定義が前面に押し出された Relational Theory には、作成されたデータモデルの妥当性の検証や、そもそも、モデル化対象(これも曖昧)から、何を Relation とするべきか、どう分割するべきかという指針は、明確には提示されていません。このあたりを補強するのに、概念モデリングは必ず役立ちます。
Relational Theory の正規化されたサンプル Relation を概念情報モデルで書いてみる
折角なので、前述の正規化された Relation(表)として図示したものを概念モデルで書いてみることにします。
前のセクションで説明した通り、概念情報モデルは、ある一つの”意味の場”を対象に作成します。Wikipedia をはじめ、参考にした資料群は、どんな”意味の場”に対して Relation を作成したか曖昧(そもそも Relational Theory にはそういう概念無いからね)なので、”意味の場”をどう設定するかで、モデルが全く異なってきますが、ここでは私の想像の範囲で”意味の場”の概要を決めてモデル化することにします。
図4. ボイス・コッド正規化の例
概念情報モデルは下図の通り。

”意味の場”としては、商品購入の際のお役立ち情報を想定しています。Product、Shop、Most Famous Shop の3つの概念クラス、及び、R2 で、元の Relation を再構成できます。もちろん、ボイス・コッド正規化の条件を満たしています。
この概念情報モデルでは、単なる Relation の定義だけだと曖昧だった情報に関する制約をたくさん追加しています。R2 の多重度が、両方とも”0..1”にしています。これは、Product の中には一押しの店が無い場合があること、逆に、Shop の中には一押しの Product がない場合があること、かつ、ひとつの Product に対して、一押しの Shop は一店しかないないこと(何しろ一押しだからね)を意味します。もともとの Relation 群の定義では曖昧だった制約が明確化されています。
図7. 第四正規化の例
次は、第四正規化された例として挙げた Relation に対する概念モデリング結果です。”意味の場”としては、ざっくり、”教育コース管理”としました。

ここでは、一行に沢山のカラムが満載の Relation を正規化の観点で分割していくという視点よりも、モデル化対象の意味の場にどんな概念群が存在していて、それらはどんな意味的関係があるかという視点でモデルを作成しています。もともとの表では Course の行の値が、三文字の英文字で表現されていますが、現実の教育コースなら、必ず、一読して内容がある程度わかるような名前がついているはずです。講師については、同姓同名の人がいることを考えれば、講師名だけで構成できるはずはないので、教育コースを提供する組織における ID 的な特徴値の”教員ID”(”講師ID”の方が適切かもね)を追加する、等を行っています。図書も同様ですね。
R1、R2 共に、両端の多重度が”*”と、0の場合を許しています。これにより、参考図書がないコース、講師が割り当てられていないコースが存在することを許しています。逆に、コースが割り当てられていない参考図書、コースに割り当てられていない講師の存在も然りです。なんでそうしているかというと、意味の場が、”教育コース管理”としていて、私の中では、コースの計画工程もこの意味の場に含むことにしているからです。どんなコースを提供するか、誰にそのコースを担当してもらうか、どんな図書が必要かを検討する間は、R1、R2 の Relationship をひな型にしたリンクを作成すること(リンクを作成する=割り当てること)はできませんから。
意味の場が”コース受講者管理”なら、講師が割り当てられていないコースは存在しえないはず(モデル作成者がそう決断し、ステークホルダー達もその考えに同意したということ)なので、R2 の講師側の多重度は”1..*”が妥当になります。
いずれにしろ、このケースでも、単なる Relational Theory の定義では曖昧だった状況が明確になり、かつ、モデル化対象の現実世界(意味の場)に存在する”何か”との対応付けも明確になっています。
概念モデリングの途中で、第四正規化のことは一切考えていませんが、結果的に第四正規化の制約は満たしているはずです。
図8. 第五正規化の例
続けて、第五正規化の例について概念モデリングを行った結果を示します。
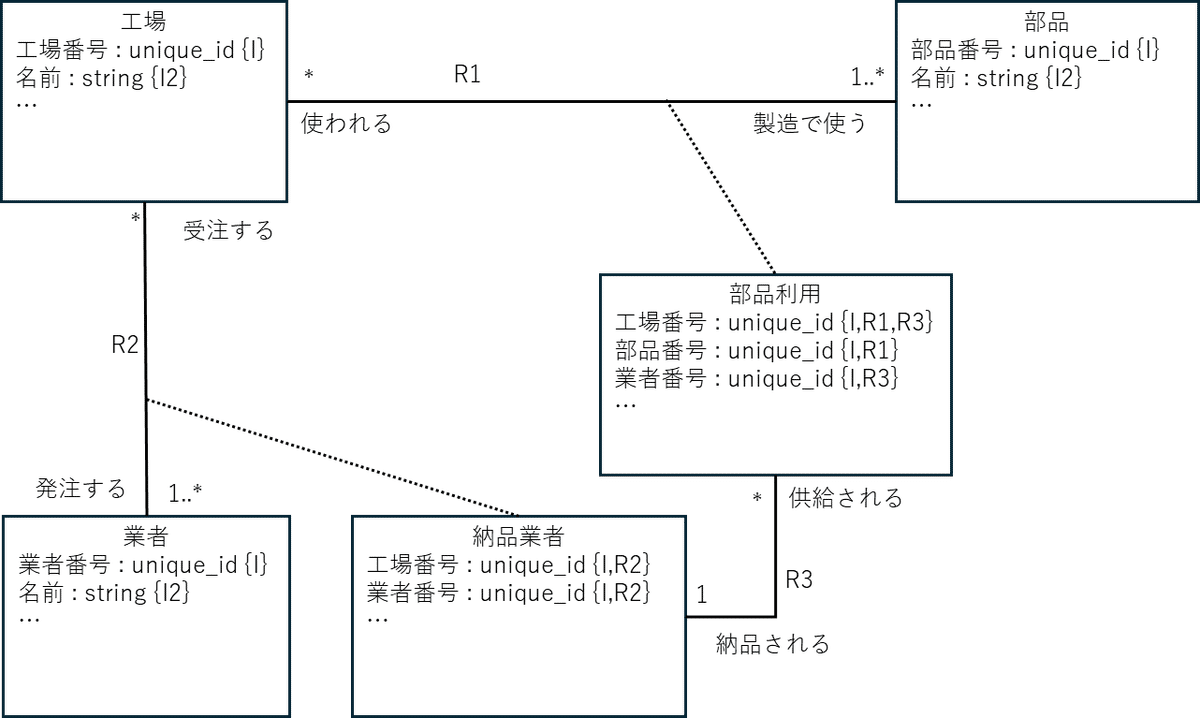
ここでは、”意味の場”として、”製造に必要な部品の受発注管理”を設定しました。R1、R2、R3の多重度は、色々な意図をもってあえて、図の多重度にしています。例えば、R1 の工場側の多重度は、”*”になっているので、工場では製造で使わない部品も存在が可能になっています。なぜ?それは、ある工場が、四半期ごとに製造する製品を変えていて、製品ごとに使う部品の組が変わるからって事。そういう意味では、この概念情報モデルには、”製品”というクラスも追加すべきなんでしょうけどね。今回は省略。
他の多重度についても、この多重度の場合、どういう制約が生まれるか考えてみてください。
第四正規化の時と同様、この概念情報モデルを作る時に、第五正規化の制約は意識せず、”意味の場”だったらこうだろうなという概念の抽出にフォーカスしています。結果としては、第五正規化を満たすモデルが出来上がっているので、概念モデリング流の概念情報モデルを妥当に作っていくと、結果として、そのモデルを Relation 群に変換すると、第五正規化を満たすようになるのかもしれませんね。
「意味の場が曖昧過ぎませんか?」ですと?
はい、そうですね。でも、実務的にも原理的にも、”意味の場”の説明を書くときは、ある程度の曖昧さは問題ありません。
何故なら、”意味の場”を厳密に記述したものが、”概念モデル”=”概念情報モデル”+”概念振舞いモデル”なのですから。
”意味の場”を明確に文章で説明しようとすればするほど、概念モデルが記述する内容を、形式が定まらない誤解を生みがちな自然文でだらだらと書いていくことになってしまいます。
実務においても、”意味の場”の説明は、2~3行で十分です。誰かにもう少し具体的に説明してと言われたら、3つぐらいの、想定されるシーンのポンチ絵を描いて説明するのが良いプラクティスです。
更に緻密に詳しく説明しろと言われたら、概念モデルを読んでください、と言いましょう。
意味の場で異なるデータ型
図9~11で紹介した概念情報モデルでは、識別子を意味する特徴値(Relation ではキー属性)のデータ型を ”unique_id” としました。このデータ型は、その概念クラスをひな型に存在する概念インスタンス(Relational Theory では Relation(テーブル)の行に相当)のその特徴値の値は全て異なることを意味します。それ以上でもそれ以下でもありません。図10 の Product や Category、Shop に相当する対象世界のモノを思い浮かべてください。対象世界においてはそれらに明確な番号はついていません。単に人間がそれぞれの Product や Category、Shop を区別できているだけです。その事実を表しているのが、識別子特徴値であり ”unique_id” であるということです。モデル化対象の意味の場において、図10の ”図書” の ”ISBN-NO” の様に識別用に特別な意味を持っている特徴値以外は、単にそれぞれの概念インスタンスが異なることを示す値であるという unique_id という方で十分です。
一方で、図9~10のモデルを実際の Relational Database に実装する場合には、unique_id を integer(自動的に1づつ増えていく)や、GUID(Global Unique ID)などの唯一性が保証された string(TEXT 型とした方が妥当かも)等、どれを使うか決定が必要です。integer、string は、Relationa Database の意味の場に属する概念であり、実装においては、図9~10 のそれぞれの意味の場を対象に作られた概念情報モデルとの対応付けがなされます。
Entity Framework を使う場合には、対応付けは、C# の Entity Framework の意味の場との対応付けをすることになります。
この対応付けは、Entity Framework と Relational Database の間でもなされています。
最後に
ここまでついてきてくれた読者の皆さん、難解な解説を読んでくれてありがとうございました。
今回は全て無料で読めるようにしました。
私の最初の目論見、「専門家ではない一般人にも分かるように書く」は、見事に失敗してますね。難しい。。。
この記事が、皆さんのモデリングライフの助けになれば幸いです。
さてと。。。Relational Theory に関する詳細な記事も書いたので、そろそろ例の記事、書き始めるとするか…
ここから先は
Azure の最新機能で IoT を改めてやってみる
2022年3月にマイクロソフトの中の人から外の人になった Embedded D. George が、現時点で持っている知識に加えて、頻繁に…
この記事が気に入ったらチップで応援してみませんか?
