曲がった座標の物差し

　真偽は不明なんですが，以前数学の先生が書かれた本の話．

　京都のように，碁盤の目状に道路が通っている街に住んでいる人は，道順を説明するときに例えば，

「二条通りを西」

というように，通りの名前と東西南北で言うのに対し，東京のように環状道路が通っている町に住んでいる人は，

「3つ目の信号を左」

というように，目印と方向で言う傾向があるそうです．

　その先生曰く，前者が「直交座標人間」で，後者が「極座標人間」だそうです．

　あなたはどちらでしょうか？私は専ら

「あの通りをあっち方向」

という一般化座標人間です．

　ということで，今回もベクトルとテンソルの話の続きです．

　前回の記事はこちら，

「共変成分」と「反変成分」の話でした。

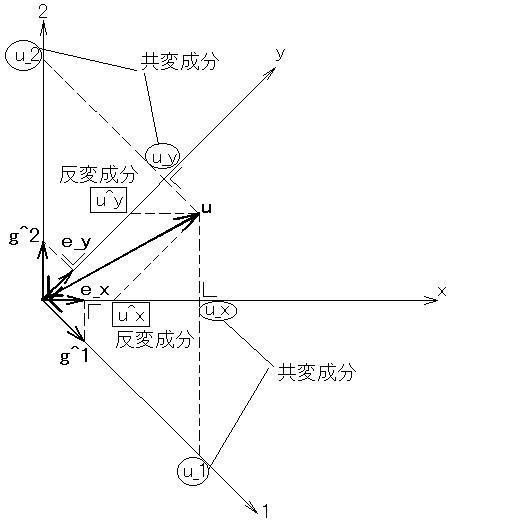
[fig. 1]（また別ウィンドウで開いておくと便利です）

　さて，改めて確認すると，「基底ベクトル」の方も

"e_x", "e_y", "g^1", "g^2"

と，

「下付き，上付き添字」で表されて

います．これは，

基底ベクトルにも「共変，反変」の区別

があり，それぞれ

「共変基底ベクトル」，「反変基底ベクトル」

と呼んでいます．

　共変基底ベクトルの方は，

x-y斜交座標系に固定した「単位ベクトル」

でした．すなわち，

このベクトルの向きは常に「座標軸の方向」

であって，座標変換に伴い，

座標軸と共に方向を変換される

わけです．ひとつ注意すべきことは，共変ベクトルは一般的に、座標変換で長さが変わりますが，この場合は「単位ベクトル」なので，

大きさは「単位長さ」で一定

です。（物差しの長さは座標変換しても変わらない）

　それに対して反変基底ベクトルは，座標変換に伴い，

2つのベクトルの「なす角」が，

「2つの共変基底ベクトルのなす角」が小さくなればなるほど，

それに反して大きくなって行く

ことが．[Fig.1]から分かると思います．

　大きさについては先ほどと同様，それぞれ

「x, y軸」から「1, 2軸」に投影した長さ

になっていて，

単位長さが変わっている

点に注意して下さい．（物差しが伸縮する．）

　こちらの場合は，共変基底ベクトルが一定（単位長さ）であっても，

その投影の方向によって伸縮

しています．

　また，もうひとつ重要な事があります．ベクトル"u"を表すのに，

u = u^x e_x + u^y e_y
　　= u_1 g^1 + u_2 g^2

という2つの式が考えられるのですが，

前者は「反変成分と共変基底ベクトル」
後者は「共変成分と反変基底ベクトル」

という組み合わせになっているという事です．

　ベクトルを2つの方向に分解する時は，必ずこのように

「共変」「反変」のペア

になります．

「成分」と「基底ベクトル」のうち，

どちらを「共変」させてどちらを「反変」させるか

という問題であると考えればごくごく自明な事なのですが，共変成分か反変成分かというのは，

1つのベクトルをそれぞれ別の立場から眺めた時の違い

と言うことができると思います．

　さて，「反変基底ベクトル」は上記の通り，

共変基底ベクトルの，それが固定されている座標軸に垂直な投影

ということで定義されるわけですが，

共変基底ベクトルそれ自体が，座標の変化によってどの様に変化していくか

を，今度は極座標で見てみましょう．

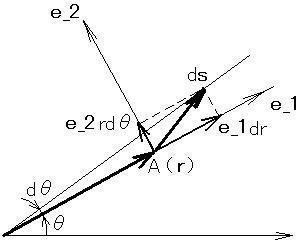
[Fig.2]（別ウィンドウで表示すると便利です）

　[Fig.2]は，

極座標(r,θ)上の「線素ベクトル"ds"」

を示しています．

　「線素ベクトル」とは，曲線の長さを測るときに，

真っすぐな短い物差しを用意して，部分的に直線とみなして測る

イメージです．

"ds"を「r（半径）方向」と「θ（円周）方向」に分解した成分

で考えると，

ds = (dr, r dθ)

となり，

線素ベクトルの始点を原点に取った単位ベクトル

を使って，

ds = e_1 dr + e_2 r dθ --- ( i )

と書くことができます．ここで，新たに基底ベクトル

g[1] ≡ e_1
g[2] ≡ r e_2

を取ると，( i )式は

ds = dr g[1] + dθg[2]

と書きなおすことができます．

　ここで，

基底ベクトル"g[1]"は単位ベクトルそのまま

ですが，"g[2]"は「絶対値"r"」をもち，2つのベクトルの方向は，

"θ"に従って時々刻々と変化

しています．したがって，ここで取った

「局所座標系」の基底ベクトル"g[1]", "g[2]"は，

座標系と共に変換される「共変基底ベクトル」

である事がわかります．また，それに対応して成分

ds = (dr, dθ)

は「反変成分」である

と言えます．従って，その共変・反変を分かりやすくするため，

g[1] → g_1
g[2] → g_2
dr → d(x^1)
dθ→ d(x^2)

と置きなおして（置き換えが多いデスが，ひとつづつ落ち着いて考えてください），

[Fig.1]の「x-y斜交座標系」

のときと同じような形式のベクトル表現

ds = d(x^1) g_1 + d(x^2) g_2

が得られます．

　[Fig.2]で，

ベクトル"r"を伸縮させると，"ds"も伸縮する

ところを想像してみてください．確かに，

"g_1"と"g_2"が共変基底ベクトルである

ことが確認できると思います．

　リーマン幾何学で出てる局面座標の共変ベクトル，反変ベクトルは，このように、

座標とともに変化する物差しで測ったか、

長さや方向が固定された物差しで測ったか

の違いであるということです．

　ここまで理解できて，私はようやくその先に進む気になりました．それは大学の期末テスト一週間前の事でしたが，これが納得できなかったら単位を落としていたことでしょう．．．

　ということで，ベクトルとテンソルの話は終わりです．

　そろそろあっちであれしてくるので，この辺で．