「タル」と「トロ」では全然違う

　昔、ボストンに出張に行った際、イタリア料理店に入った時の事。

　日本ではどんな小さな飲食店に入っても、だいたいメニューに写真がついていたり、表に食品サンプルが飾ってあったりしますよね。でも、今でもそうなのかわかりませんが、アメリカのレストランて写真付きのメニューを出してくれるところって、ほとんどないんですよ。

　それで、そもそも英語すらあやしかった私でしたが、何とか苦労してパスタを注文する事は出来たんです。とりあえず「ナントカーノ」って感じの名前を探して注文したら、たまたま当たってたんですけど。

　ちなみにそれは、トマトと魚介のソースですごい美味しかったんです。未だに何を頼んだんだか思い出せないんですが。

　問題はデザートでした。「ティラミス」はあまり好きではなく、「パンナコッタ」は知っていたので、「ナントカッタ」って感じのする名前を探して注文したんです。

　そうしたら、お肉が出てきちゃったんです・・・。多分、

「パンナコッタ」と「パンチェッタ」

を間違えたんでしょうね。なんてこった。

　それ以来、

「似た名前から推測するのは止めよう！」

と思いました。

　ということで、

「エントロピー」と紛らわしい「エンタルピー」

が出てくる話になります。前回は「定積熱容量」

Cv = (∂U/∂T)v

を定義しました。

　これは、「定積過程」では、

系に与えられた熱がそのまま「内部エネルギ」の増加になる

ということから、こう書くのでした。

　それでは「定圧熱容量」というものを考えてみたいと思います。

　ちなみに、「定圧」とか「等圧」とかいろいろ入り混じって使っているかもしれませんが、その日の気分です（おい）。

　えらーい学者先生が、同じことを意味する科学用語を統一しようともせずに使うのですから、我々学習者は、いろいろな呼び方に慣れておく必要があるのです。

●定圧熱容量とエンタルピー

　定圧過程というのは文字通り、

系が外界と一定の圧力の下で熱をやり取り

して、「体積変化」する過程です。これは、下図のように考える事が出来ます。

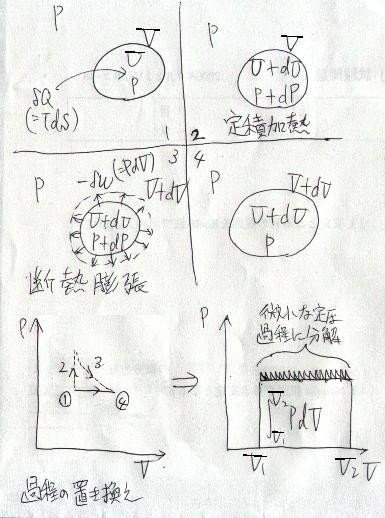
　「定圧」とは具体的には、

系の内部圧力が、外界の圧力と釣り合っている状態

と言えます。すなわち上のマンガでは、

微小な熱を受け取る
↓
内部エネルギーが無限小増加し、外界より無限小、内圧が上がる
↓
系が無限小膨張し、外界に微小な仕事をする
↓
系の内圧と外界の圧力が釣り合う

（「無限小膨張する」という考え方については、以下の記事もご参照ください。）

　これは形式上、「定圧過程」が「定積過程」と「断熱過程」に分解できる事を示しています。これに従って、

定圧下での温度変化あたりの入熱量

すなわち「低圧熱容量"Cp"」は、以下のように考えられます。

Cp = (δQ/dT)p --- ( 1 )

　エネルギー保存則により、

系が受け取った熱"δQ"

は、

δQ = dU + PdV --- ( 2 )

と、内部エネルギーの増加と外界への仕事に使われるので、( 1 )式は、

Cp = {(∂U + P∂V)/∂T}p --- ( 3 )

ということになります。

　ちなみに前回は、

⊿Q = C⊿T

Cv = ⊿U/⊿T

と、分かりやすいように「変化」を表す"⊿"を使って書きましたが、厳密には

温度によって比熱が変わってくる

ので、正確にはこのように、「微小変化量」をあらわす

"δ"（状態量でない時）

"d"（状態量の「微分」を表す時）

を使うべきです。

　ただ、気体では分子間の相互作用が弱いため、実際には比熱の変化はほとんど無視できます。

　どうしても気になるという人は、前回の式に

lim[⊿T→0]

とでも付け加えといてください。

　ここで、ちょっとした数学的テクニックを使います。「積の微分」

 (fg)' = f'g + fg'

より、「微小量」を表す"d"は、状態量の積"PV"に対して

d(PV) = PdV + VdP

とできます。しかし、

「定圧」過程では圧力"P"の変化が無い

ので、

dP = 0

です。( 3 )式において、

P(∂V/∂T)p

というのはすなわち

{∂(PV)/∂T}p = P∂V/∂T + V∂P/∂T

で、「定圧」なので、

V∂P/∂T = 0

です。なので、

Cp = {∂(U + PV)/∂T}p

と書いても同じです。ここで出てきた

"U + PV"

を、新しい「状態量」

H≡U + PV

で置き換えてやります。これが「エンタルピー」という状態量です。

　改めて「エンタルピー"H"」という量を使うと、「定圧熱容量"Cp"」は、

Cp = (∂H/∂T)p

と書けるわけです。

●２つの熱容量と変数変換

　ここでちょっと、「エンタルピー」の物理的意味は置いといて、式の上でどう変わったのかに注目してみます。「定積熱容量"Cv"」は、「内部エネルギ」

U = U(T,V)

を使って、

Cv = (∂U/∂T)v

と書けました。「定圧熱容量"Cp"」は、「エンタルピー」

H = H(T,P)

を使って、

Cp = (∂H/∂T)p

と書けました。つまり、

U
↓
H = U + PV

と、"U"に"PV"を加えることで、独立変数を"V"から"P"に変換していることになります。こういう変数変換を、「ルジャンドル変換」と言います。

　話を元に戻して、もう何度も言っていますが、「定圧過程」で温度を上げようとしたら、

「定積過程」より「仕事"PdV"」の分、余計に熱が必要

で、それが

「熱容量」の大きさに反映されている

という事です（下図）。

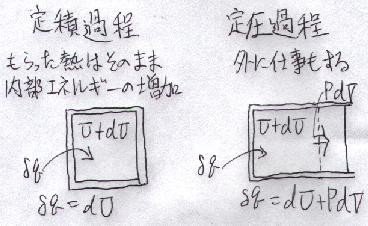
　「エンタルピー(enthalpy)」はギリシア語で「温まる」という意味です。つまり、大気圧下で空気を「温める」時は、

「熱膨張の仕事」も考慮しなければならない

ということで、こういう量が考えられたのです。

■「ルジャンドル変換」という手法

　ルジャンドル変換は「解析力学」に出てくるので有名です。

　「ラグランジュの運動方程式」は、「ラグランジュアン」

L = T - U

（"T"「系の全運動エネルギー」、"U"「系の全ポテンシャルエネルギー」）

を使うと、

「一般化運動量"p[i]"」、「一般化座標"q[i]"」

として、

p[i] = ∂L/∂q'[i]
p'[i] = ∂L/∂q[i]

（"p', q'"は時間微分）

と書けますが、ここで「ハミルトニアン」

H≡Σp[i]q'[i] - L = T + U

（すなわち「系の全力学的エネルギー」）

を導入してルジャンドル変換すると、

q'[i] = ∂H/∂p[i]
p'[i] = -∂H/∂q[i]

という「ハミルトンの正準方程式」を得ます。

　エネルギの観点で物理現象を考察する場合は、途中の具体的変化を考えず、とにかく

ある過程の前後の状態を表わす数式

が得たいわけです。それで、記述を高度に「抽象化」して、こういった解析的手法を活用するのです。

　これは、物理数学の「数学的側面」と言えるのかもしれません。

　ここまで抽象化された場合は、数式を「物理的意味」から考察しようというのは、逆にナンセンスかもしれません。いちいち物理的意味を気にする必要無く、

普遍に成り立つ式をわざわざ用意

して、数学のテクニックを使えるようにしてあるからです。

　エネルギ変換の過程を

「微視的プロセス」に置きかえる

のではなく、こうして抽象化されたままで数式を扱う感覚に慣れておく事も、「エネルギ物理」の習得には大切な事です。