思考タイプ別の方程式解法
「あなたの性格診断します」
というのは、私は信用しません。何故なら、
人の性格なんて、その時の状況や立場でいくらでも変わる
からです。
それを、
「あの人はこういう性格の人だ」
と、他人をより単純に理解するために、人はレッテルを張りたがるのです。
その行為に、私は意味があるとは考えません。
●「思考タイプ」は一定の分類ができる
しかし、性格という漠然としたものではなく、得意とする思考方法については、一定の分類ができそうです。それは主に、
①記憶している事を頼りにして答えを出すタイプ
②ロジックを考えて答えにたどり着くタイプ
③ひらめきで答えを出すタイプ
の3つです。
これは、どれが優れているという問題ではなく、この分類により、
「どういう勉強方法が適しているのか」
がわかるのです。
それでは、
「自分はこのうちのどれに当てはまるか」
という判定方法ですが、これは
「方程式の解き方」
でよく分かるのではないかと思います。
●連立一次方程式の解法
「連立一次方程式」の解法には、主に以下の3つがあります。
①クラメルの公式
②ガウスの消去法
③代入法と加減法の組合せ
例えば、以下のような連立一次方程式の解を求める事を考えます。
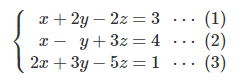
①「クラメルの公式」を使う場合
クラメルの公式は、まず
「未知数 "x", "y", "z" の係数」と「右辺の定数」からなる行列
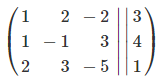
を考えます。そして、
「未知数の係数だけの行列」の行列式
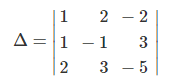
を求めます。
行列式は、以下のように計算します。
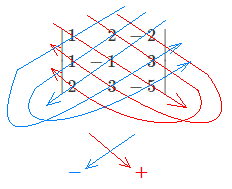
ものすごく説明を端折ると、上図のようにたすき掛けをして、その結果を方向により+-の符号を付けて、
Δ = { 1×(−1)×(−5)+2×3×2+(−2)×3×1 } − { (−2)×(−1)×2+2×1×(−5)+1×3×3 }
= 8
とします。
そして、x を求めたい場合は、「未知数の係数だけの行列」の
「x の係数を定数で置き換えた」行列
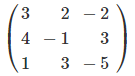
の行列式を計算して、
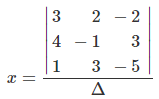
とすれば、x は
x =
[{ 3×(−1)×(−5)+2×3×1+(−2)×3×4 } − { (−2)×(−1)×1+2×4×(−5)+3×3×3 }]/8
= 1
と求まります。
同様に、y と z も
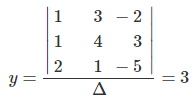
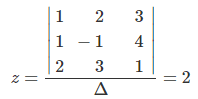
と求まります。
この方法は、「行列式の計算」と「列の置換」の方法さえ覚えてしまえば、あとは機械的にこれに当てはめれば誰でも解ける方法です。
②「ガウスの消去法」の場合
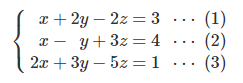
に対し、
(2)式-(1)式
(3)式-(1)式×2
をすると、
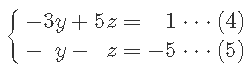
となり、
(5)式-(4)式÷3
をすると、
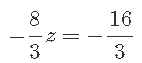
となり、
z = 2
と求まります。これを (5)式 に代入すれば、
-y -2 = -5
y = 3
さらに (1)式 に y, z の値を代入すれば、
x + 6 - 4 = 3
x = 1
と求まります。これは、
「上の式を使って、下の変数を順番に消していく」
というロジックさえ理解していれば、機械的に解ける方法です。
③「代入法と加減法の組み合わせ」の場合
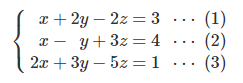
に対し、例えば、
(1)式-(2)式
をすると、
3y - 5z = -1 ・・・ (6)
(3)式-(6)式
をすると、
2x = 2
x = 1
と求まり、
(1)式+(2)式×2
をすると、
3x + 4z = 11 ・・・ (7)
(7)式に x = 1 を代入して、
4z = 8
z = 2
(6)式に z = 2 を代入して、
3y - 10 = -1
y = 3
と求まります。これは、式を見て
「(1)式-(2)式をすれば x が求まる式が出てくる」
と気が付かないとできない方法です。
●一通りやってみて得意な方法を選択する
このように、方程式の解法は、思考タイプ別にあった解き方があります。なので、その人の思考に合った解き方を身につければよく、教える側はその選択肢を示してあげるのがいいと思います。
そして、最初に学ぶときは、同じ問題をいろいろな解き方で解いてみて、どの解き方が一番しっくり来るかによって選ぶと、勉強の成果が出やすくなるのではないかと思います。
ちなみに、私は方程式に限らず、1つの問題について思いつく限りの解き方をマスターして、ものの見方の幅を広げるトレーニングをしています。
ちなみに今回の数式は、"HostMath" という
Microsoft の「数式エディタ」のような感覚で、「LaTeX コマンド」を入力して数式を作成できるサイトを利用して作成してみました。
