【数学】多項式関数の微分積分

こんにちは、Junです。

前回は、微分積分の定義について書きましたが、
今回は、その中でも最も簡単な、多項式関数の微分・積分について書いていきます。

前回のnoteを見られていない方は、

をチェックしてから本noteを読むことを推奨します。

⒈　多項式関数

の形で表される関数のことを多項式関数といいます。

⒉ 　多項式関数の微分

では、nを0以上の整数とするとき、

の微分を考えましょう。

この関数を、微分の定義の式

に当てはめてみると、

二項定理で展開して、

Δxに0を代入して、

したがって、

また、指数が負の場合、つまり逆数の場合を考えてみましょう。

-n=kとおくと、

したがって、任意の整数nについて、

が成り立ちます。

例）

ちなみに、定数を微分すると0になります。

⒊ 　微分の線形性

関数

があるとき、

が成り立ちます。

微分の定義に、af(x)+bg(x)+ch(x)を当てはめてみれば、線形性を証明できます。（証明してみてください）

例）

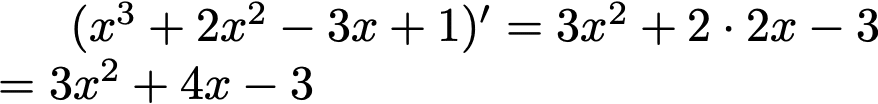
⒋ 　多項式関数の練習問題

では、練習問題を出します。

次の関数を微分しなさい。

（1）

（2）

（3）

（4）

⒌ 　多項式関数の積分

nを整数（但し-1でない）とするとき、

であるから、

但し、Cは積分定数

※n=-1の場合については、後日紹介します。

例）

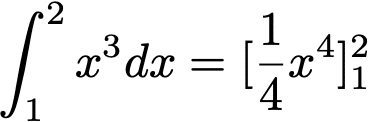
⒍　積分の線形性

の原始関数がそれぞれ

であるとき、

これも、微分の線形性から容易に示せます。

例）

⒎　多項式関数の積分の練習問題

では、練習問題を出します。

次の積分計算をしなさい。

（1）

（2）

（3）

（4）

⒏　まとめ

今回は、多項式関数の微分・積分について説明しましたが、他にもいろいろな関数の微分・積分があります。

その他の関数に関する微分・積分は後日説明しますが、まずは基本的な多項式関数の微分・積分を覚えておけば、受験生であれば、共通テストにも役立ちますし、一般の方も比較的抑えやすい内容になっていると思います。

#数学がすき #数学 #微分 #積分 #多項式関数 #mathematics #calculus #differentiation #integration #polynomialfunction