
【数学】置換積分(特殊置換)
こんにちは、Junです。
前回は、基本的な置換積分について書きましたが、
今回は、特殊な置換をする置換積分について書いていきます。
⒈ ルートの中がa^2-x^2の形の関数の積分
例
以下のような形の積分を考えます。
$$
\int_{0}^{a}\sqrt{a^2-x^2}dx (a > 0)
$$
この積分は、少し特殊な変数置換を行います。
$$
x=a\sin \theta (-\frac{\pi}{2}\le\theta\le\frac{\pi}{2})
$$
とおくと、
$$
dx= a\cos \theta d \theta
$$
となり、
$$
x:0\to1 \\ \theta : 0\to \frac{\pi}{2}
$$
したがって、
$$
\int_{0}^{a}\sqrt{a^2-x^2}dx=\int_{0}^{\frac{\pi}{2}}\sqrt{a^2-a^2\sin^2\theta}a\cos\theta d\theta
$$
$$
=\int_{0}^{\frac{\pi}{2}}a^2\cos^2\theta d\theta
$$
$$
=\frac{a^2}{2}\int_{0}^{\frac{\pi}{2}}(1+\cos2\theta) d\theta
$$
$$
=\frac{a^2}{2}[\theta+\frac{1}{2}\sin2\theta]_{0}^{\frac{\pi}{2}}
$$
$$
=\frac{1}{4}\pi a^2
$$
となります。
上記のような積分において、$${x=a\sin\theta}$$とおくのは、
$${y=\sqrt{a^2-x}}$$とおいて、両辺の2乗すると、
$$
y^2=a^2-x^2\\x^2+y^2=a^2
$$
となり、原点$${O}$$中心の半径$${a}$$の円であることがわかります。
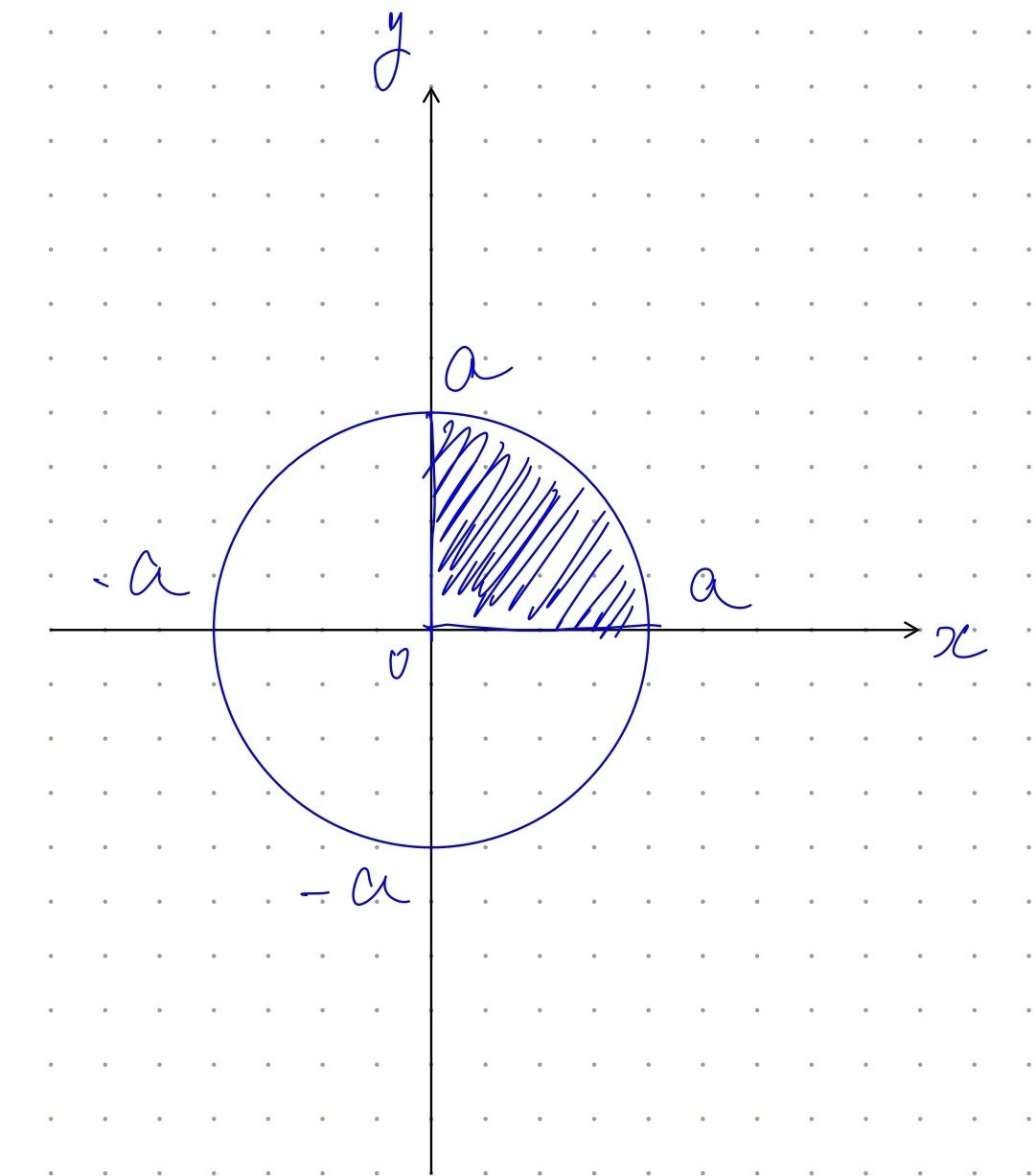
この円を、媒介変数$${\theta}$$を用いて、
$$
\begin{cases} x=a\cos\theta \\ y = a\sin\theta\end{cases}
$$
または、
$$
\begin{cases} x=a\sin\theta \\ y = a\cos\theta\end{cases}
$$
と表せるからです。
$${x=a\cos\theta}$$とおいてもできるのですが、一般的には、$${x=a\sin\theta}$$とおきます。
練習問題
以下の積分を計算しなさい。
(1)
$$
\int_{0}^{2}\sqrt{4-x^2}dx
$$
(2)
$$
\int_{0}^{1}\frac{1}{\sqrt{1-x^2}}dx
$$
(3)
$$
\int_{2}^{\frac{4+\sqrt{2}}{2}}\sqrt{-3-x^2+4x}dx
$$
(3)のヒント:ルートの中を平方完成してみてください。
⒉ 分母にx^2+a^2の形がある関数の積分
例
以下のような積分を考えます。
$$
\int_{0}^{a}\frac{1}{x^a+a^2}dx (a > 0)
$$
この場合は、
$${x=a\tan\theta(-\frac{\pi}{2}<\theta<\frac{\pi}{2})}$$とおくと、
$$
dx=\frac{a}{cos^2\theta}d\theta
$$
となり、
$$
x:0\to a \\ \theta:0\to \frac{\pi}{4}
$$
となるので、
$$
\int_{0}^{a}\frac{1}{x^2+a^2}dx=\int_{0}^{\frac{\pi}{4}}\frac{1}{a^2\tan^2\theta+a^2}\frac{a}{\cos^2\theta}d\theta
$$
$$
=\int_{0}^{\frac{\pi}{4}}\frac{1}{a^2(\tan^2\theta+1)}\frac{a}{\cos^2\theta}d\theta
$$
$$
=\int_{0}^{\frac{\pi}{4}}\frac{\cos^2\theta}{a}\frac{1}{\cos^2\theta}d\theta
$$
$$
=\frac{1}{a}\int_{0}^{\frac{\pi}{4}}d\theta
$$
$$
=\frac{1}{a}[\theta]_{0}^{\frac{\pi}{4}}=\frac{\pi}{4a}
$$
となります。
上記のような積分において、$${x=a\tan\theta}$$とおくのは、
$$
(\tan \theta)'=\frac{1}{\cos^2\theta}
$$
であることと、公式
$$
1+\tan^2\theta=\frac{1}{\cos^2\theta}
$$
を利用して、式から$${\cos^2\theta}$$が消えてしまうことで、計算がしやすくなるからです。
練習問題
以下の積分を計算しなさい。
(1)
$$
\int_{0}^{2}\frac{1}{x^2+4}dx
$$
(2)
$$
\int_{-1}^{0}\frac{1}{x^2+2x+2}dx
$$
(2)のヒント
分母の$${x^2+2x+2}$$を平方完成してみてください。
⒊ ルートの中がx^2+aの形の関数の積分
例1
以下のような積分を考えます。
$$
\int\sqrt{x^2+a}dx
$$
被積分関数が$${\sqrt{x^2+a}}$$の形を含んでいる場合、
$${t=x+\sqrt{x^2+a}}$$とおくと、うまくいきます。
$$
t-x=\sqrt{x^2+a}
$$
として、両辺を2乗すると、
$$
(t-x)^2=x^2+a
$$
$$
t^2-2tx+x^2=x^2+a
$$
$$
2tx=t^2-a
$$
$$
x=\frac{1}{2}(t-\frac{a}{t})
$$
となり、
$$
dx=\frac{1}{2}(1+\frac{a}{t^2})dt
$$
より、
$$
\sqrt{x^2+a}=t-x=t-\frac{1}{2}(t-\frac{a}{t})
$$
$$
=\frac{1}{2}(t+\frac{a}{t})
$$
このもとで式を変形すると、
$$
\int\sqrt{x^2+a}dx=\int \frac{1}{2}(t+\frac{a}{t})\frac{1}{2}(1+\frac{a}{t^2})dt
$$
$$
=\frac{1}{4}\int(t+2\frac{a}{t}+\frac{a^2}{t^3})dt
$$
$$
=\frac{1}{4}(\frac{1}{2}t^2+2a\log|t|-\frac{a^2}{2t^2})+C
$$
(定積分の場合は、ここでtの値を入れて結果を出します。)
$$
=\frac{1}{4}\{\frac{1}{2}(t^2-\frac{a^2}{t^2})+2a\log|t|\}+C
$$
$$
=\frac{1}{4}\{\frac{1}{2}(t-\frac{a}{t})(t+\frac{a}{t})+2a\log|t|\}+C
$$
$$
=\frac{1}{4}(x\cdot2\sqrt{x^2+a}+2a\log|x+\sqrt{x^2+a}|)+C
$$
$$
=\frac{1}{2}(x\sqrt{x^2+a}+a\log|x+\sqrt{x^2+a}|)+C
$$
となります。
このパターンのポイントは、
$${t=x+\sqrt{x^2+a}}$$と、置換の仕方を覚えてしまうことです。
例2
もう1つ例をやってみましょう。
$$
\int\frac{1}{\sqrt{x^2+a}}dx
$$
まず、例1と同じように$${t=x+\sqrt{x^2+a}}$$とおきます。
そうすると、
$$
dt=(1+\frac{2x}{2\sqrt{x^2+a}})dx=\frac{\sqrt{x^2+a}+x}{\sqrt{x^2+a}}dx
$$
$$
=\frac{t}{\sqrt{x^2+a}}dx
$$
$$
\frac{1}{t}dt=\frac{1}{\sqrt{x^2+a}}dx
$$
となるので、式を変形すると、
$$
\int\frac{1}{\sqrt{x^2+a}}dx=\int\frac{1}{t}dt
$$
あとは積分すればいいので、
$$
\int\frac{1}{t}dt=\log|t|+C=\log|x+\sqrt{x^2+a}|+C
$$
となります。
別解
$${a>0}$$の時、別解として、
$$
x=\frac{\sqrt{a}(e^t-e^{-t})}{2}
$$
とおいても計算できます。
この方法で例2と解いてみます。
$$
x=\frac{\sqrt{a}(e^t-e^{-t})}{2}
$$
とおいて、これを$${t}$$について解くと、
$$
e^t-\frac{2}{\sqrt{a}}x-e^{-t}=0
$$
両辺に$${e^t}$$をかけて、
$$
e^{2t}-\frac{2}{\sqrt{a}}xe^t-1=0
$$
$$
(e^t-\frac{x}{\sqrt{a}})^2=\frac{x^2+a}{a}
$$
$$
e^t=\frac{x}{\sqrt{a}}\pm\frac{\sqrt{x^2+a}}{\sqrt{a}}=\frac{x\pm\sqrt{x^2+a}}{\sqrt{a}}
$$
$${e^t>0}$$であるから、
$$
e^t=\frac{x+\sqrt{x^2+a}}{\sqrt{a}}
$$
$$
t=\log|\frac{x+\sqrt{x^2+a}}{\sqrt{a}}|=\log|x+\sqrt{x^2+a}|-\log|\sqrt{a}|
$$
ここで、
$$
dx=\frac{\sqrt{a}}{2}(e^t+e^-t)dt
$$
$$
\sqrt{x^2+a}=\sqrt{\frac{a}{4}(e^{2t}-2+e^{-2t})+\frac{4a}{4}}
$$
$$
=\frac{\sqrt{a}}{2}\sqrt{(e^{2t}+2+e^{-2t})}
$$
$$
=\frac{\sqrt{a}}{2}\sqrt{(e^{t}+e^{-t})^2}
$$
$$
=\frac{\sqrt{a}}{2}(e^{t}+e^{-t})
$$
これらより、
$$
\int\frac{1}{\sqrt{x^2+a}}dx=\int\frac{2}{\sqrt{a}(e^{t}+e^{-t})}\frac{\sqrt{a}}{2}(e^t+e^-t)dt
$$
$$
=t+C
$$
$$
=\log|x+\sqrt{x^2+a}|-\log|\sqrt{a}|+C=\log|x+\sqrt{x^2+a}|+C
$$
($${-\log|\sqrt{a}|}$$は定数なので、$${C}$$にまとめました)
$${x=\frac{\sqrt{a}(e^t-e^{-t})}{2}}$$とおく理由は、
$$
y=\sqrt{x^2+a}
$$
とおいて、両辺を2乗すると、
$$
y^2=x^2+a \\ x^2-y^2=a
$$
すなわち、
$$
\frac{x^2}{a}-\frac{y^2}{a}=-1
$$
という、双曲線になっており、
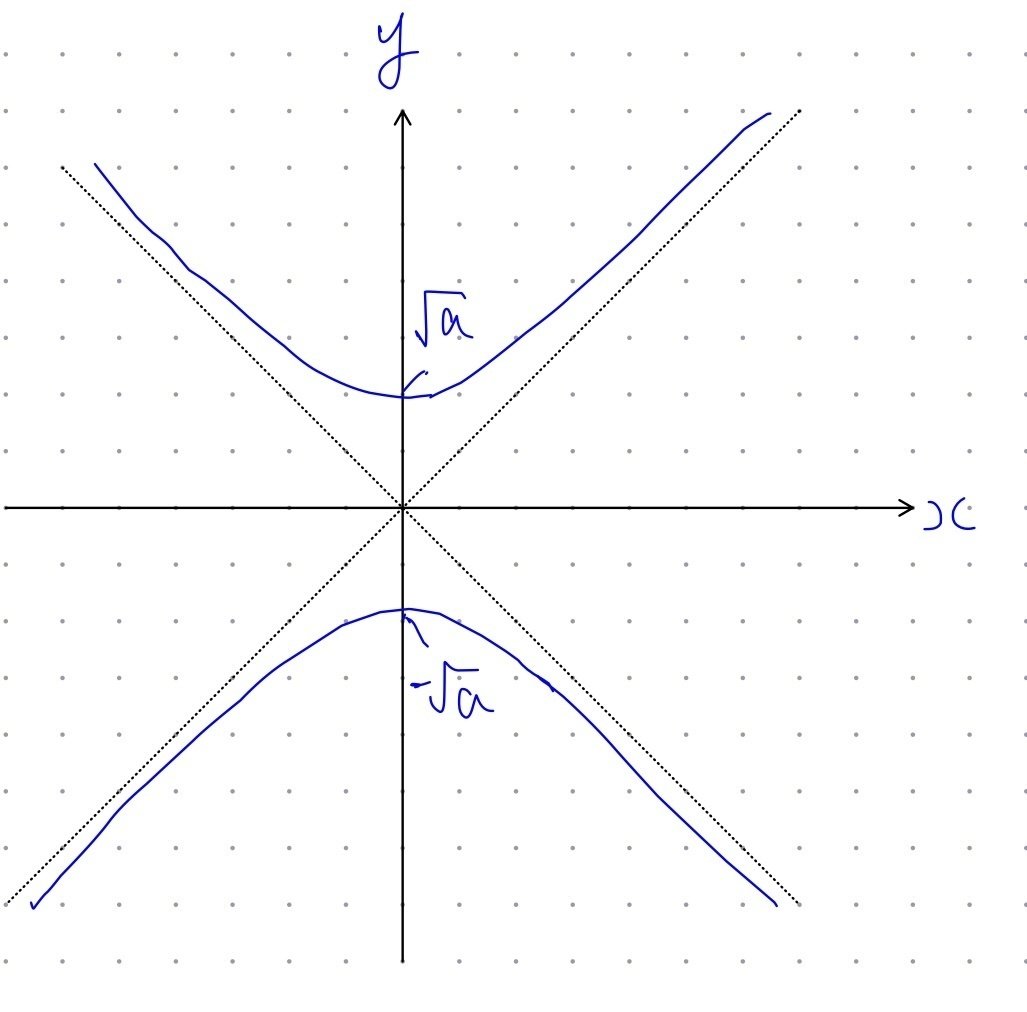
この双曲線を媒介変数$${t}$$を用いて、
$$
\begin{cases} x=\frac{\sqrt{a}(e^t-e^{-t})}{2} \\ y = \frac{\sqrt{a}(e^t+e^{-t})}{2}\end{cases}
$$
と表せるからです。
練習問題
以下の積分を計算しなさい
(1)
$$
\int\sqrt{x^2+1}dx
$$
(2)
$$
\int_{0}^{1}\sqrt{x^2+2}dx
$$
(3)
$$
\int\frac{1}{\sqrt{x^2+3}}dx
$$
(4)
$$
\int_{0}^{\sqrt{3}}\frac{1}{\sqrt{x^2+3}}dx
$$
(5)
$$
\int\frac{1}{\sqrt{x^2+6x+10}}dx
$$
(5)のヒント
$${x^2+6x+10}$$を平方完成してみてください。
まとめ
今回は、特殊な置換をする置換積分について書きました。
紹介した以外にも様々な置換積分が存在するのですが、特に覚えておいて欲しい置換積分を紹介しました。
次回は、面積と体積について書く予定です。
#数学がすき #数学 #微分積分 #積分 #置換積分 #特殊置換 #インテグラル #mathematics #calculus #integration #integral #substitution #substitute
