
行列式の二つの列を入れかえると符号が逆さま(行の入れかえでも)
行列式の二つの列を入れ替えれば、行列式の符号が変わるということを証明するために、より一般的な定理を証明します。
複素数を成分とするn次正方行列Aの列に、n次対称群S(n)の置換τを作用させると、その行列式は、行列式|A|にsgn(τ)を掛けたものに等しいということを証明します。
τとして、互換のときを考えると、互換(i, k)の符号sgn((i, k)) = -1なので、二つの列を入れ替えると行列式の符号が変わるということが証明できたことになります。
数学の証明をするときに、より一般的な命題の方が証明しやすくなるときもあります。そんなときは、証明したい命題の一般化にあたる命題を証明しておき、その後で特殊なこととして成立すると述べれば大丈夫です。
行列式の二つの列を入れ替える
n次正方行列Aのi列とk列を入れ替えてできる行列をA'とします。
このとき、|A'| = -|A|となります。

行列Aのi列とk列を入れ替えた行列の行列式は、もとの行列の行列式に-1を掛けたものに等しくなっています。このことを証明するために、より一般的な次の定理を証明します。
行列式の列を置換する
n次正方行列Aについて、n次対称群S(n)の置換τを1つ固定して、τで各列たちを置換した行列をA'とします。
このとき、|A'| = sgn(τ)|A| となります。
τとして、互換(i, k)を考えると、i列とk列の二つの列を入れ替えることになり、互換のsgnは-1なので、示したかった命題が示せたことになります。では、一般化した定理の方を証明します。
定理の証明
τ∈S(n)について、任意のσ∈S(n)に対して、
sgn(στ) = sgn(σ)sgn(τ) が成立します。
sgnは、置換が、偶数個の互換の積で表されているとき1、奇数個の互換の積で表されているときに-1を対応させる符号なので、次の4パターンのいずれであっても、等号が成立します。
①σが偶置換、τが偶置換→στは偶置換
②σが偶置換、τが奇置換→στは奇置換
③σが奇置換、τが偶置換→στは奇置換
④σが奇置換、τが奇置換→στは偶置換
起こり得る①から④のどの場合であっても、sgn(στ)とsgn(σ)sgn(τ)は等しくなります。
また、合成写像(関数)の定義から、1 ≦ r ≦ n である自然数rに対して、σ(τ(r)) = στ(r) となります。これら2つの置換に関する一般論を踏まえて、さらに、τが全単射であることから、τ(1)、τ(2)、・・・、τ(n)が、1からnを入れ替えたものであり、{τ(1), τ(2), ・・・, τ(n)}をn!通りのσで置換することを考え、A'の行列式を定義に基づいて計算していきます。

この2つ目のシグマ計算でn!個の項の加法を計算しています。
{1, 2, ・・・, n}をS(n)のn!個の置換で入れ替えてできる項で総和をとることと、{τ(1), τ(2), ・・・, τ(n)}をS(n)のn!個の置換で入れ替えてできる項で総和をとることは、加法の順番が入れ替わっているかもしれませんが、加法の交換法則から、総和が同じになります。
そのため、2つ目のシグマ計算と3つ目のシグマ計算が、項の順番が入れ替わっているだけで、n!個の総和は等しくなっています。
ここで、sgn(στ) = sgn(σ)sgn(τ)であることと、σ(τ(r)) = στ(r) (1 ≦ r ≦ n)であることとを使います。
シグマ計算のn!個の各項について、σ(τ(r))をστ(r)に変形します。
ここで、群論の入門的な内容ですが、対称群S(n)全体について、S(n)τ = S(n)となります。
これは、右剰余類S(n)τ = {στ | σ∈S(n)}について、f, g∈S(n)が異なれば、fσとgσが異なるためです。
στのσを動かすと、n!個の置換が出現します。
また、sgn(τ)は、1か-1なので、2乗すると必ず1になります。
よって、sgn(σ) = sgn(σ)sgn(τ)sgn(τ)です。
sgn(σ)sgn(τ) = sgn(στ)なので、
sgn(σ) = sgn(σ)sgn(τ)sgn(τ) = sgn(στ)sgn(τ) となります。
これらの内容をまとめると、次のようになります。

各置換σに対して、sgn(σ)sgn(τ) = sgn(στ)なので、sgn(τ)をシグマΣの外に出しました。
最後の式で、各行数を置換しているστは、先ほど述べたように、n!通りの置換です。στをfとでも置き直すと、次のようになります。

次の図で、fにn!個の置換を代入すると、やはりn!個の置換になるので、結局、シグマ計算の部分はもとの行列Aの行列式ということになります。

この最後の式は、sgn(τ)|A|です。シグマの部分が、もとの行列Aを行について置換する行列式の定義そのものです。
これで、証明が完成しました。上の図から、ここまでの式は、すべてイコール(=)なので、|A'| = sgn(τ)|A|が導けました。
よって、τとして互換のときを考えると、2つの列を入れ替えると、行列式に-1を掛けたものに等しいということが分かります。
ちなみに、行列式の定義で、行を置換しても、列を置換しても、同じ結果になります。これから、この内容の詳しい説明を述べます。
行数を置換した行列の行列式
1. 有限群の右剰余類
2. n次の行列式|A'|の計算
この順に説明します。Gを有限群として、HをGの部分群とします。そして、g∈Gを1つ固定します。
このとき、Hg = {xg | x∈H}を右剰余類といいます。この右剰余類Hgに含まれる群Gの元(要素)の個数は、Hに含まれる要素の個数と一致します。
ちなみに、gH = {gx | x∈H}を左剰余類といいます。やはり、含まれる元の個数は、Hに含まれる元の個数と同じになります。
この部分群Hとして、全体G自身を考えることもあります。このnote記事で2.の証明をするときに、Gとしてn次対称群S(n)、部分群Hとして、S(n)自身、S(n)の元としてτを1つ固定という状況を考えます。
S(n)τ = {στ | σ∈S(n)}はS(n)と一致します。このことを行列式を定義に従って計算するときに使います。行列式の定義では、n次対称群のn!個の置換をすべて当てはめてできるn!個の項の加法を計算します。
ここで、S(n)と右剰余類S(n)τが一致することから、S(n)τのn!個の置換をすべて当てはめてできるn!個の項の加法を計算して良いということになります。
|A'|の計算
ここから、証明部分になります。
複素数を成分とするn次正方行列Aについて、n次対称群の置換τで、Aの行数をすべて置換してできる行列をA'とし、τは以下でずっと固定して使います。
|A'|を計算するときに、A'の列数をS(n)で置換するという定義に基づいて計算します。

ここで、一番下のシグマΣ計算に変形できるのは、右剰余類S(n)τがS(n)と一致しているからです。n!個の項の出現する順番は替わっているかもしれませんが、複素数の加法については交換法則が成立するので、シグマ計算をしたときの総和は等しいということになります。
ここで、n次対称群の置換fとhについて、sgn(fh) = sgn(f)sgn(h)となります。sgn(f)は、置換fの符号といい、fが偶置換のときは1、fが奇置換のときは-1です。1と-1という複素数なので、sgn(f)sgn(h)とsgn(h)sgn(f)は等しい値になります。
そのため、S(n)の任意の置換σと、固定されたτについて、sgn(στ) = sgn(τ)sgn(σ)となります。n!個のどの項にもsgn(τ)が出現するため、分配法則でsgn(τ)をくくり出すことができます。
議論は、もうすぐ完成します。一番下のシグマ計算で、行数と列数のτで置換されている数字が同じになっていることに注目します。
このため、行数がτ(1), τ(2), ・・・, τ(n)となっているときに、n個の複素数の結合法則と交換法則を使って、行数が1, 2, ・・・, nの順になるように入れ替えると、次のようになります。
※στ(k) = σ(τ(k))となっています。
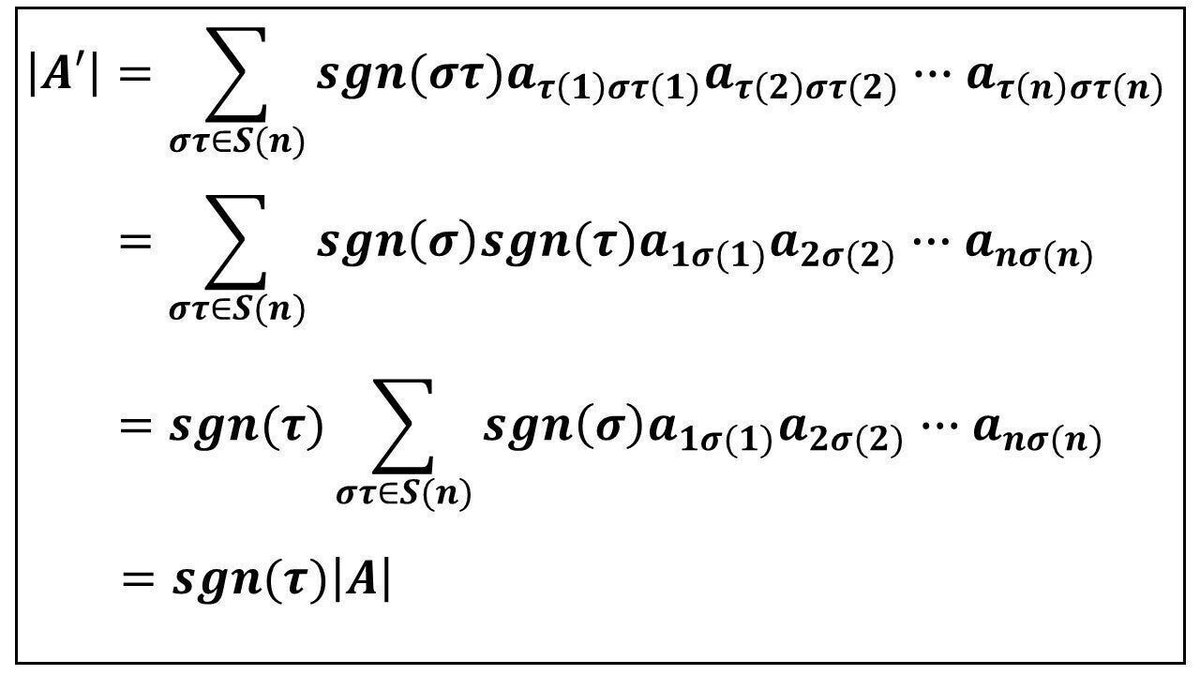
上から3番目のシグマ計算は、行列Aの行列式を列数置換する定義そのものです。そのため、|A|と書いたものが上から4番目の式です。はじめに固定したτの符号sgn(τ)が掛けられるということになります。
これで、証明が完成です。ちなみに、τとして互換を考えると、2つの行を入れかえるということになります。互換1個の符号は―1なので、行列式において、2つの行を入れかえるという基本変形をすると、行列式の値が―1倍になるということが分かります。
この記事では、列についての内容でしたが、行についても、同じようにして証明できます。行については、行列式をはじめに、列から置換する方の定義で議論を進めていきます。
具体例で見返し確認
合成写像στが出てきたあたりから、議論が複雑になってきました。抽象的なn次対称群で議論をしているので、難しい雰囲気になってしまいます。しかし、具体例で考えると、実は大したことをしていません。
n = 3のときで、3次対称群で具体的に考えてみます。
τ = (1, 3, 2)という長さ3の巡回置換として固定します。
τ(1) = 3, τ(2) = 1, τ(3) = 2 という入れ替えです。
[1, 2, 3]を[3. 1, 2]に入れ替えるのが置換τです。
また、{στ | σ∈S(3)} = S(3)なので、στをf∈S(3)と置き直します。
στのσに3!個の置換を代入すると、S(3)の置換が3!個できるので、それら3!個の置換をfに代入すると考えます。
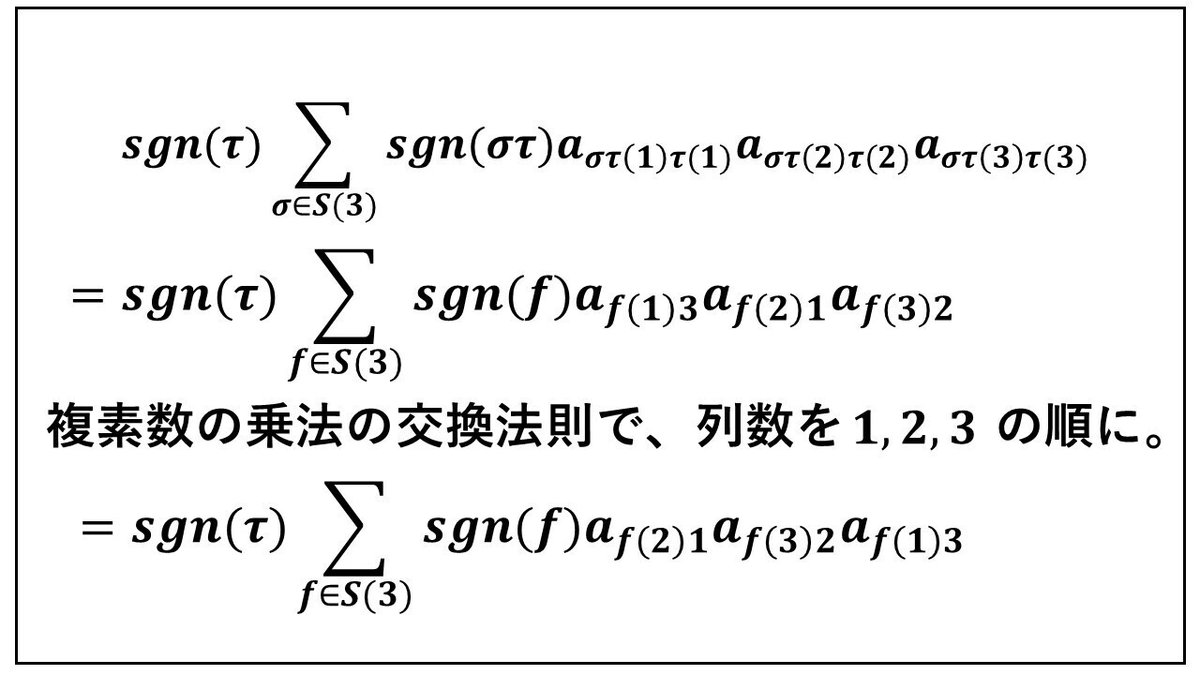
次に、{f(2), f(3), f(1)}をn! = 3!個の置換で入れ替えたときにできる順列3!個は、{1, 2, 3}をn! = 3!個の置換で入れ替えたときにできる順列3!個と同じものになります。出現する順番は異なるかもしれませんが、その順番は、加法についての交換法則を使うと同じ順番にすることができます。
したがって、今、行数がf(2)、f(3)、f(1)となっていますが、3!個の順列を配置するわけですから、h(1)、h(2)、h(3)の順にしておいても、hのところに3!個の置換を代入したときに出現する3!個の項の加法を計算するのと同じ結果になるということです。よって、次のようになります。

先ほどの証明では、τ(1)からτ(n)の値が不明だったので、逆置換を書きましたが、結局、行数をn!個の置換で置換してできるn!個の項の加法を計算するということです。
さらに分かること
もし、n次正方行列Aのi列とk列が同じだとすると、i列とk列を互換(i, k)で入れ替えた行列A'は、行列Aと同じになります。同じ行列だと、もちろん行列式の値は同じなので、 |A'| = |A| となります。
一方、先ほど証明したことから、互換で2つの列を入れ替えると、行列式に-1を掛けたものに等しくなることから、|A'| = -|A| となります。
したがって、|A| = -|A| となり、2|A| = 0 なので、|A| = 0 となってしまいます。
まとめると、n次正方行列Aの二つの列が同じとき、|A| = 0 ということになります。
変わらないパターンもアリ
転置しても行列式は変わりません。このことを4次正方行列Aの行列式|A|について、列数を4次対称群S(4)で置換することで、確認します。

4次対称群の元である置換は、異なる4個のものを入れ替える操作と考えられるので、4!個、つまり24個の置換があります。
行列式は、4変数の多項式の形の項24個の和となります。24個の置換の1つをσとして、列数を置換することを考えます。
このときに、4次対称群の置換の1つσに応じて、多項式の1つの項が形成されます。この形成する状況を可視化してみます。

列数をσで置換するので、行列Aの1行目を見て、列数がσ(1)となっているAの成分を取り出します。
その次に、Aの2行目を見て、列数がσ(2)となっているAの成分を取り出します。残りの3行目と4行目も同様に、列数がそれぞれσ(3)、σ(4)となっているAの成分を取り出します。
このようにして取り出した4個のAの成分をすべて掛け合わせると、行列式の1つの項に使われている文字の部分が決まります。
*さらに先頭にsgn(σ)というσの符号である1もしくは-1を掛けています。
sgn(σ)は、行数の置換でも列数の置換でも、それぞれの項に同じものが現れているので、文字部分が同じがどうかということに意識を向けます。
ここで、証明の決め手になる内容です。

正方行列の行列式を求めるときに、列数を対称群で置換しても、行数を対称群で置換しても、同じ値になります。このことを利用することで、転置行列の行列式が同じ値になることが示されます。
転置行列の行列式
転置行列も同じサイズの4行4列の行列式です。ややこしいので、各成分を表す文字をbを使っています。
転置行列の定義から、転置行列の(i, j)成分の値は、もとの行列Aの(j, i)成分の値と同じになっています。
この転置行列の行列式は、行数を対称群で置換することで求めます。

この行数を対称群で置換して、行列式を求めるときに、先ほどと同じ置換σについて、どのように1つの項を決定するかを確認します。

転置行列の1列目を見て、行数がσ(1)となっている転置行列の成分を取り出します。
2列目から4列目まで、同様に、行数がそれぞれσ(2)、σ(3)、σ(4)となっている成分を取り出します。
このようにして得られた転置行列の4個の成分をすべて掛け合わせると、行列式の1つの項に使われている文字の部分が決まります。
ここで、転置行列の成分について、行数を表す添え字iと列数を表す添え字jを入れ替えると、もとの行列Aの(j, i)成分になることが効いてきます。

転置行列の1列目から4列目まで、それぞれ同じ行列Aの成分が並んでいます。
そのため、σという置換で選んだ多項式の項の4個の文字の部分について、行列Aの列数置換と転置行列の行数置換で、全く同じになっています。
したがって、転置行列の行列式と、もとの行列Aの行列式は、同じ値になっています。

これで、証明が完成しました。この証明ですが、4次でなく、n次にして同様のことを書くと、一般のn次正方行列についての証明になります。
具体的な置換で確認
先ほど、「σという置換で選んだ多項式の項の4個の文字の部分について、行列Aの列数置換と転置行列の行数置換で、全く同じになる」ということを述べました。
このことを、σに具体的な置換を当てはめて確認します。
σが(1, 3, 2, 4)という長さ4の巡回置換のときを考えます。
この置換は、σ(1) = 3, σ(2) = 4, σ(3) = 2, σ(4) = 1 という置換です。
行列Aは列数を置換し、転置行列は行数を置換しました。上で書いたアルゴリズムの通りに、多項式の文字部分を取り出してみます。

σ = (1, 3, 2, 4)について、Aの行数置換と転置行列の列数置換で取り出した1個が、同じAの(1, 3)成分となっています。
残りの3個についても、確認してみます。まず、2と3について、行数置換と列数置換を確認します。σ(2) = 4、σ(3) = 2 について、同じAの成分を選んでいることが分かります。

転置行列の(4, 2)成分は、もとの行列Aの(2, 4)成分です。そして、転置行列の(2, 3)成分は、もとの行列Aの(2, 3)成分です。
|A|のσについての項に関して、1列目から3列目の添え字を置換した文字と、転置行列の1行目から3行目の添え字を置換した文字が同じになっていることが分かりました。
残りのσ(4) = 1 についても確かめ、σに応じて現れる行列式の項を見比べてみます。

これで、σについて、aの方で列数置換をして選んだ4個の文字と、bの方で行数置換をして4個の文字が同じということが分かりました。
どちらも、行列Aの(1, 3)成分、(2, 4)成分、(3, 2)成分、(4, 1)成分をすべて掛け合わせていることになります。
どちらも同じ置換なので、sgn(σ)はどちらも同じですから、σに応じて出現する項は、全くの同じものということになります。
24個の4次対称群S(4)の置換のそれぞれについて、同様のことが起きていて、結局、24個の項の和である行列式は、同じということになります。
これが、転置行列の行列式と、もとの行列の行列式が同じになることの仕組みです。
関連するnote記事
次の記事は、基本変形と余因子展開を使って4行4列の行列式を具体例を通じて求めることを説明しています。行列式を求めるために必要な理解が揃ってくると、アウトプットに良いかと思います。
また、独自ドメインのサイトもありまして、こちらではベクトル空間の公理に関連する基本事項を解説しています。
