
1点からその球に2本の接線を引いたとき接点までの距離は等しい~そして楕円~
中学数学で、直角三角形の合同条件を学習します。これは、平面図形の内容ですが、空間図形を考えるときに、垂直に交わる2直線が出てきたときなどに、使うときもあります。このnote記事では、球外の1点から、その球に引いた2本の接線引いたとき、球外の1点から接点までの距離がどちらも同じ長さになっていることを証明します。
平面図形について、円外の1点から、その円に2本の接線を引いたときに、円外の1点から接点までの距離がどちらも等しいことを、直角三角形の合同条件を使って証明をします。
実は、空間図形の内容ですが、球外の1点から、その球に引いた2本の接線引いたとき、球外の1点から接点までの距離がどちらも同じ長さになることを、同じ要領で証明できます。この考え方の応用例として、円錐を斜めに平面で切断したときの断面が楕円になるということを証明しています。

まず、復習に、直角三角形の合同条件を述べておきます。
直角三角形の合同条件
【条件a】
直角三角形の斜辺と他の1辺がそれぞれ等しい
【条件b】
直角三角形の斜辺と1つの鋭角がそれぞれ等しい
この【条件a】か、【条件b】のどちらかに当てはまれば、2つの直角三角形は合同となります。合同は、ぴったりと重なり合うということです。重なり合う辺の長さどおしは等しい長さで、重なり合う角の大きさは等しい角度になるということです。このnote記事では、以下の議論で、【条件a】の方を使います。
球外の1点から2本の接線を引いたとき

球外の1点Pから、2本の接線を引き、2つの接点が点Aと点Bです。球外の1点から接点までの距離というのは、2点を結んだ線分の長さのことなので、PA = PB となることを証明したいわけです。
ここで、球の中心Oと接点を結んだ線分は、接線と接点において垂直に交わるということを使います。
空間図形を見ていると、ややこしいので、平面をピックアップして考えるのがオススメです。今回は、3点PとAとBを通る平面の上で、議論を進めていきます。
球の対称性として、直線POについて、対称な図形になっているという結果にもなります。次の図をご覧ください。
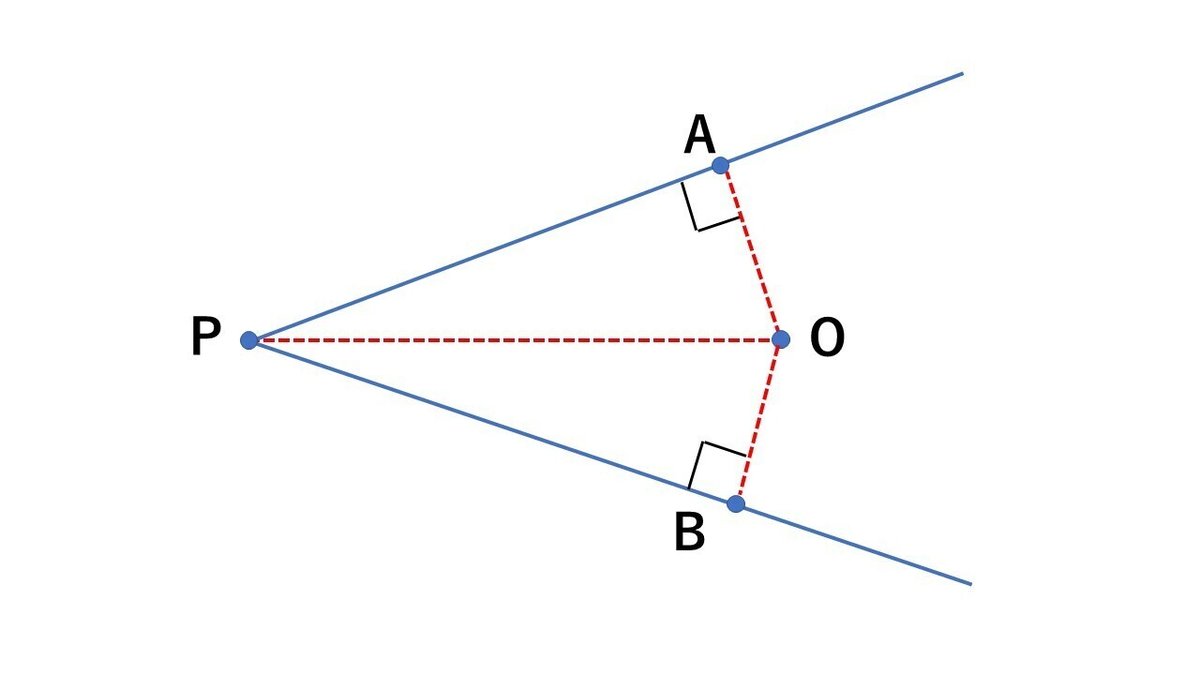
先ほどの空間図形から取り出した平面図形です。△PAOと△PBOが合同「≡」ということを示せれば、重なり合うPAとPBの長さが等しいことを結論づけられます。
合同の証明をするときに、OAとOBは、どちらも球Oの半径だったので、同じ長さになっていることに注意です。それでは、直角三角形の合同条件の【条件a】を使って、最終的にPAとPBが等しいことを導きます。
【PA = PB の証明】
△PAOと△PBOについて、
∠OAP = ∠OBP = 90°・・・①
共通の辺より、PO = PO ・・・②
球の半径は等しいから、OA = OB ・・・③
①、②、③より、直角三角形の斜辺と他の1辺がそれぞれ等しいので、△PAO ≡ △PBO
よって、重なり合う辺の長さが等しいため、
PA = PB 【証明終了】
これで、証明が完成しました。この球外の1点から2つ接線を引いたときに、球外の1点から接点までの距離がどちらも等しいことは、しばしば空間図形の問題で使われるので、押さえておくと良いかと思います。
高校数学の理系の内容で楕円が出てきます。空間図形に関連して楕円が出るときに基本になる内容を書いておきます。
円錐の平面による切断と楕円

図のように、円錐Oに2つの内接球が接しています。上の内接球と円錐の接点がMで、下の内接球と円錐の接点がM'です。この円錐を平面αで切断したときの断面が図の黄色の部分です。円錐Oと平面αとの交線を緑の線にしています。黄色の周りが緑の交線になっています。
そして、平面αと上の内接球との接点がF、平面αと下の内接球との接点がF'です。
このとき、緑の交線上の任意の点Pに対して、2定点FとF'からの距離の和が一定になります。つまり、PF + PF' が一定となります。2定点からの距離の和が一定である図形というのが楕円の定義です。この2定点が、点Fと点F'で、この2定点を楕円の焦点といいます。
結論から書くと、PF + PF' の値は、線分MM'の長さと常に等しくなります。このことを示すのに、先ほどの球外の1点から接線を引いたときに、接点までの距離が等しいということを使います。
<楕円である理由>
母線OPと2つの内接球との接点をそれぞれM, M'です。上側の内接球と平面αは点Fで接し、下側の内接球と平面αは点F'で接しているので、PFとPF'は、それぞれの接線です。
また、PMと上側の内接球との共有点は点Mだけなので、PMは上側の内接球の接線です。同じくPM'は、下側の内接球の接線です。
したがって、点Pから上側の内接球に引いた2本の接線がPFとPMなので、球外の1点と2つの接点までの距離が等しくなることから、PF = PM となります。
同様に、PF' = PM' です。
よって、線分の長さについて、次のようになります。
PF + PF' = PM + PM' = MM'
MM'は、はじめから定点Mと定点M'を結んだ線分の長さなので、長さは一定です。このことから、2定点F, F'と緑の枠線上の任意の点Pを結んだ線分の長さの和が一定なので、緑の枠線の図形は楕円ということになります。
これで、今回の記事の内容を終了します。
数IIIの公式を使った接線の求め方については、こちらのブログ記事で解説しています。
では、これで失礼します。
