東北大理系数学2006
東北大理系数学2006の解答解説です。
現在の学習指導要領では、行列を含まないので、行列の問題(大問5)は解説していません。
大問1 図形と方程式
不等式の表す領域は、おそらく図示できるでしょう。
問題は、aの最大値、最小値です。これは、図を描かいて、しばらく位置関係を考えてみると、少しずつわかってきます。

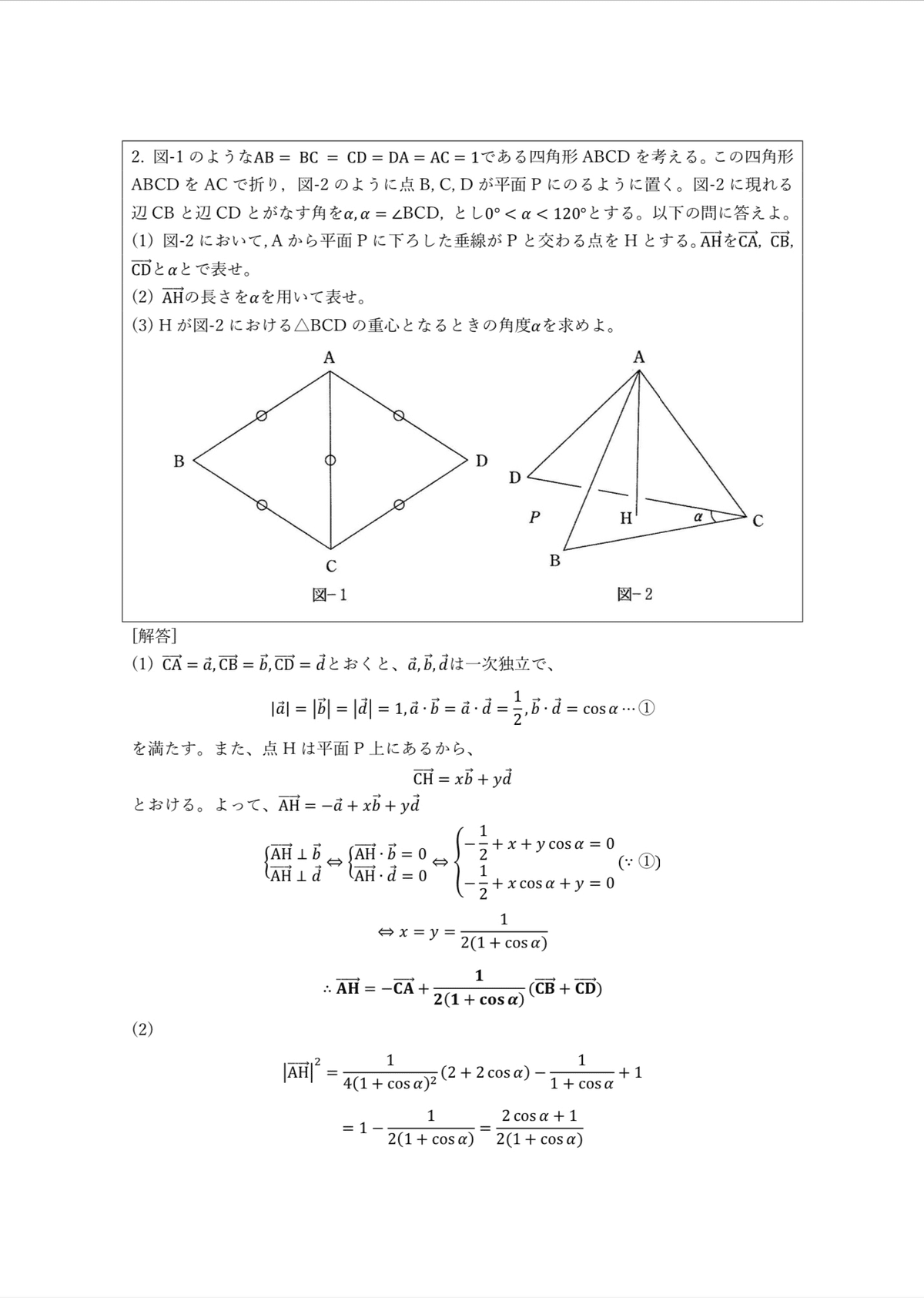
大問2 空間ベクトル
これは(1)ができれば、自動的に(2)、(3)もできていく問題です。
(1)のポイントは、点Hが平面P上にあるという条件の表し方で、基本的です。
多くの受験生が、解けた問題でしょう。

大問3 期待値
(1)と(3)はできると思いますが、(2)は小数点第三位以下を考える際に、物理のような近似を2回使います。これは、なかなか厳しい発想じゃないかなと思います。
(1)から順に解いていって、(2)で詰まってしまい、(3)を解けなかった受験生もいるかもしれません。
このようなケースもあるので、解けるところから探して解くというのは重要です。

大問4 極限(関数)
これは関数の増減と極限の非常に綺麗な問題で、著者も解いているときに、楽しかったです。
一貫して重要なことは、単調性です。単調性さえわかれば、その関数の端点を調べるだけで、関数の取り得る値の範囲がわかります。
(1)は単調性とπ/2での値から示します。
意外に重要なのが、(2)です。cos kπ=(-1)^k という公式を知らない人が結構いるんじゃないかなと思います。(著者も実際、高3の夏に学校の先生に教えてもらって、初めて知りました。)これは、単位円を考えたら明らかで、覚えておくとかなり得をします。特に、(-1)^k=cos kπ と使えると超便利です。
(3)は、定番の、「単調性と中間値の定理」から、f'(x)=1となる点がただ1つであることを示す問題です。
(4)は(3)の不等式から、はさみうちの原理でx_n→0(n→∞)なので、xsin (π/x)のx→0の極限を考えればよく、一方、そもそもsinは-1から1だから、ここでもはさみうちの原理より、極限が求まります。


大問6 二次関数、積分
(1)は、二次関数と領域Dとの位置関係を図示して、正確に解いてやります。
(2)では、(1)で使わなかったa=1のときを場合分けとして使って面積を正確に計算します。
(3)では、(2)でaの値によって、異なる関数が出てきますが、同じ増減表に描いてやるというのが、一つのポイントで、こうすることで、S(a)が全体としてどのような動きをするのか、というのがわかりやすくなります。


解答解説に問題だけのページをつけ、pdf化したものです。
のちに、youtube のほうに解答解説をさらに詳しく解説した動画をupする予定です!
また、補足説明や類題演習も考えていますので、よければフォロー、いいね等お願いします。
また、解説で分かりにくい箇所等、ございましたら、気軽にXにdmか、コメントお願いします!
