リズムの生成文法
いろいろな音価の音符の並びを文字列と捉えることでリズムを形式言語の文字列として扱うことができます。
生成文法の観点からリズムを理解するためのおおまかなアイデアを書いておきます。
形式言語理論と音楽のリズムの関係
形式言語
形式言語学における「言語」とは文字列の集合のこと
形式言語では言語を文字列の集合と定義しています。「形式」というのは意味を考えないということです。
文字列というのは、例えばa, b, cという3つの文字を、同じ文字を繰り返し使ってもいいので適当に並べたものです。文字列は例えば、a, b, c, ab, ba, bc, cb, ca, ac, aa, bb, cc, aab, aba, baa,…..などと無限に考えることができます。
このような文字列を適当に集めてまとめたものが言語と呼ばれます。ごく一部を集めてもいいですし、あらゆる可能な文字列を集めても、それぞれ別の言語となります。
しかしこのままでは、ただ材料となっているアルファベットが同一というだけの規則性のない雑多な集合体に過ぎません。
このようにして考えられたいろいろな「言語」において、その言語を構成する文字列のメンバーを単純な規則で全部得られるようなものは特別な言語であると言えるでしょう。
そのようなルールはその言語がどんな文字列の集合であるかを完全に決定することになります。つまり、その言語を定義しているということです。このようなルールを「文法」と言います。
形式文法
文法には「書き換え規則」というものが使われます。
出発点を示す記号をSとします。Sを書き換えるルールをうまく作ることで文字列の集合を生み出すことができます。
ここでは大文字はまだ書き換えられる文字、小文字はもう書き換えられない文字ということにしましょう。
S→aというルールは、aという1つの文字列しか生み出さないルールです。この言語はaという文字列を1つしか持たない言語です。しかしこれも1つの言語であることには違いはありません。
S→Aaというルールは、何回適用しても大文字のAを消すことができません。ですからA→aというルールも追加しましょう。これでaa, aaa, aaaa, aaaaa,…という文字列を集めた言語が生み出されました。
このようにしてルールに様々な工夫を加えることによって、様々なタイプの「言語」つまり文字列の集合を生み出すことができるのです。
文字列としてのリズム
音楽の音符の種類を文字と考えれば、リズムパターンは文字列ということになります。
例えば4分音符をc、8分音符をqとすれば、cqqcqqは次のようなリズムパターンを意味することになります。cやqなどを使わず直接音符で考えても全く同じことです。

しかし単に音符を適当に並べたものは、音楽的なリズムになるとは限りません。そこで音楽的なリズムを生成するような文法を考えることにしましょう。最終目標は、音楽的なリズムだけを生み出すような文法を明らかにすることです。
(※ただし、この「書き換え規則による文字列の生成」というのは、数学的に考えられた生成方法であって、人間がこれと全く同じ方法を使っているということを保証するものではありません。私は人間が部分的にこれとよく似た方法を使っているだろうと想定しています。ですからある部分はこの方法による生成で説明しつつも、全てをこのような規則で説明しようとはしません。)
リズムの生成文法
リズムの文法その1——単純な拍節構造
では文法を考えましょう。
実際の音楽で使われているルールを考えます。例えば次のルールは、音楽で使われているものではありません。音楽の実情によく合致するルールを選ぶ必要があります。

次のルールは全音符を2つの2分音符に書き換えるルールです。ルールは適用してもしなくても良いので、全音符を出発点とした場合、このルールによって2種類のリズムパターンが生成されることが分かると思います。

次のルールを採用すれば3拍子を得ることができます。ここでは出発点を全音符に固定したのでこのような表現になりました。
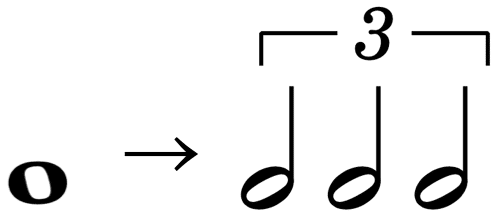
このようにしてルールを取捨選択することによって、様々な拍子構造が表現できることが分かると思います。
例えば次の2つのルールを選択すれば6/4拍子となるでしょう。(出発点を全音符としたので通常の6/4とは違う書き方になっています。)

このルールの適用によって次の4通りのリズムパターンを生成することができます。

6拍子と3拍子の違い
右の3つのパターンはすべて、一番左の全音符の性質を継承した子孫です。さらに右の2つのパターンは、2分音符2つのパターンの性質を継承しています。だから、4分音符が6つになってもそれは2拍子の性質を継承した6/4拍子であって、3/2拍子ではないと言えるのです。
次のルールは4分音符を2つの8分音符に書き換えるというルールです。このルールを上記の6/4拍子のルールに追加しても、6/4拍子であることを逸脱することはありません。

次のルールと選択可能としてもいいでしょう。やはり6/4拍子であることから逸脱することはありません。

このようにして、拍節構造に一致するような基本的なリズムパターンを生成することができます。
(※5拍子をどこで扱うべきかという問題があります。私は、5分割を基本的な生成ルールに組み込むべきではないと考えています。5分割が2分割や3分割と同類の基本的な分割だとは全く思えないからです。もし同類ならば、世の中には5拍子の曲がもっと溢れていたことでしょう。5分割は恐らく、4分割や6分割のゆがんだものとして理解されているのではないでしょうか?)
リズムの文法その2——より複雑な拍節構造
その2で扱うのは不等分割です。しかしそのためにまず、等分について改めて考える必要があります。
実は等分は難しい
音符を2つや3つに等分するということをこれまで言ってきましたが、音符の半分の長さというのはどうやれば知ることができるのでしょうか?
幾何学で、線分の中点を求めるためにはコンパスを使って垂直に交差する線を引く必要があったことを思い出して下さい。半分の長さというのは簡単には分からないものなのです。
つまり次のような2分割のルールというのは「2等分する」という意味のルールだとすると、人間の能力では運用できないということになります。

ですから人間には、「およそ半分」とか、「およそ3分の1」といった量を把握する能力が生まれつき備わっているとするか、あるいはかなり幼いときにそれを身につける、と考えざるを得ません。
よって、上記の「2等分のルール」は、実は「全体から半分を測り取る」というルールであることになります。
半分を1つ量り取れば、残りは大体半分なのでもう測る必要はありません。同様にして「3等分のルール」は、「全体から3分の1を2回測り取る」というルールとなります。
単純比
さて、このように考えると、「比較的単純な比率」やその単純な組み合わせであれば人間は容易に把握できる、と考えることができるでしょう。ですから、5分割や7分割は把握が困難で、4分割や6分割は把握が容易であることがこのことによって説明することができます。
ここで問題になるのは、比較的単純な比率というのは1/2と1/3だけなのか?ということです。
古代ギリシャのリズム論では、単純な比率を(1:1)、(1:2)、(2:3)の3つ、あるいはそこに(3:4)を加えて4つに限定していました。3分の1は、(1:2)と(2:3)を組み合わせて作ることができます。
単純な比率に(2:3)を追加することで、より複雑なリズムを、拍節構造の拡張として作ることができます。
カテゴリー:音楽理論
