音楽の拍節とフレーズ —時間構造の認知理論—(1)
(本研究のアプローチを端的に述べるとすれば『「ものの区分についての一般的な認知システム」を仮定し、音楽の時間区分をその認知システムの1つの対象と考えることによって、音楽構造の認知的な基礎を確立する』ということになる。)
第1部 認知スキーマとしての拍節構造
第1章 拍節構造とは何か
第1節 拍節構造の認知的起源
小節はどこにあるのか?
近代的な記譜法で書かれた楽譜においては、五線を縦に貫く線(小節線)の間がそれぞれ小節(measure, bar)と呼ばれている。この小節の区間を構成する主要な単位の音符は拍(beat)であり、この拍の数や拍をなす音符の種類によって小節は種類分けがされ、その種が拍子(meter)と言われる。例えば図1-1.1では、1小節に4分音符が4つ含まれているので、4分の4拍子(4/4)であるということになる。これらは、近代のいわゆる「普通の実践による音楽(common-practice music)」を構成する最も基本的な時間構造であり、同じ拍子の小節が繰り返されることによって規則的な構造を作る。ここではこのような構造を一般的に拍節構造と呼ぶことにしよう。

だが実際のところ音楽を聴く際に聴き手は、小節を区切るこの縦の線が楽譜のどこにあるのかを直接的に知ることはできない。もしも小節が聴き手にとって不可欠なものであるならば、聴き手は何とかしてそれらの位置を把握しなくてはならないことになる。よって作曲家と演奏家は、聴き手が小節線の位置を把握できるように、音楽に何らかのシグナルを与える必要が生じる。
音の強さによるアクセントは、この目的のために極めて便利な道具だ。なぜならこの種のアクセントは、音の長さや音色の違いによるアクセントとは異なり、音楽の構造にほとんど変更を加えることなしに、まるで目印を付けるかのように付与することができるからである。試しに、好きなメロディーの様々な位置に自由に強さのアクセントを付けて見ていただきたい。どのようにアクセントを付けても我々は元のメロディーが分からなくなるなどという心配はほとんどない。しかし音の長さを変えたり、音色を変えたりする場合にはそうはいかない。
音の強さによるアクセントは、その強さの度合いの違いによって拍の階層的なレベルの違いを表現できると考えられてきた。図1-1.2はアクセントを用いた表示の例である。図1-1.2のズルツァー(J. G. Sulzer)では4段階、図1-1.3のマルクス(A. B. Marx) では6段階もの区別がされていることが分かるだろう。
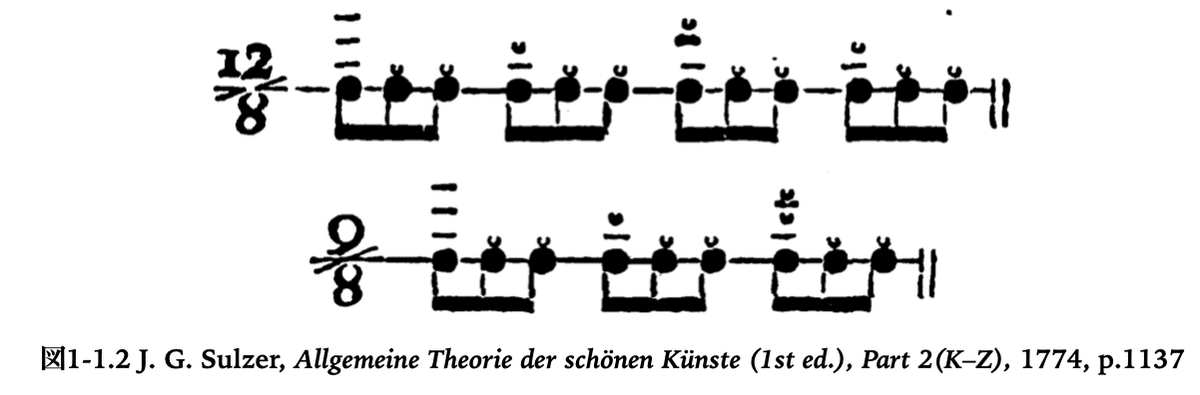
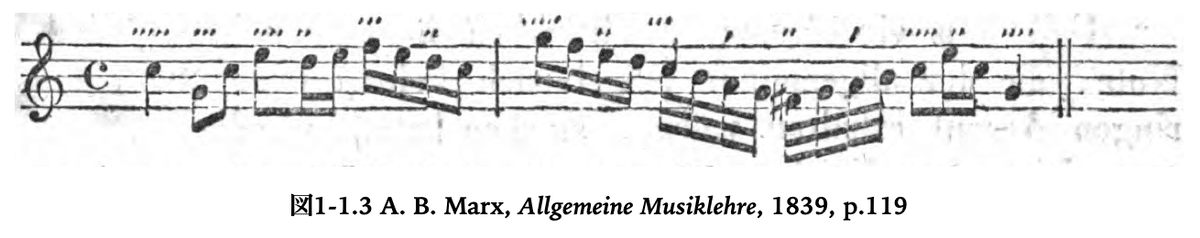
だがここで、1つの前提を見落としてはならない。それは、たとえ音の強さの違いがあっても、聴き手がそれを小節と認識しなければ、それは小節として機能しないということだ。音の強さの違いのパターンそれ自体は人間の外に存在するものである。音楽の刺激における強い拍の規則性は、小節として理解される可能性を持っているに過ぎない。だから、刺激そのものを拍節構造と同一視して論じることが可能になるのは、音の強さの違いが必ず特定の拍節構造を聴き手に認識させるという前提があってのことなのである。例えば、言語においてgetという文字の並び、あるいはその発音された音声は、読み手や聴き手がそれを英語のgetという言葉であると認識して初めて英語のgetとしての効力を持つ。我々がこの文字列や音声それ自体を英語のgetと同一視できるとすれば、それは人がそれを必ず英語のgetと識別するという前提においてのみである。言語学ではその文字列が英語のgetという動詞であると理解されるはずであるという想定の元で、その文字列をその単語自体と同一視して議論が行われるだろう。だが音楽では、この文字の画像認識に当たるレベルから考慮する必要がある。音は人間抜きに音楽にはならない。椅子や机のような物体は、その物体自体が人間と独立してある性質を持っている。だが人間の認識なしには椅子や机の機能を持つことはない。これらは人間によって椅子や机として使用される可能性を与えられた人工的な物体である。同様に音楽の刺激の配列は、人間による解釈の可能性だけを持った、人間の認識を離れてそれだけでは音楽的な性質を何も持たないただの物理的な存在である。
多くの理論家たちはこれまで、あたかも音楽の刺激の中にすでに完全な状態の小節が存在するかのように誤解してきた。アクセントが拍節を示すシグナルであるという約束事が成立しているとみなせる場合ならばアクセントという刺激の存在を拍節そのものと同一視できるかもしれないが、これは刺激の違いが反応の違いに直接対応するという極めて行動主義的な仮定である。しかしこれでは、我々がどのようにしてそうした刺激から拍節という認識を得るのかという過程についての考察を不可能になってしまう。なぜならば、アクセントあるいはその配置が強拍や拍節構造を示す記号のようなもの理解されてしまうからである。例えば、椅子なのか机なのか分からない絵があるとしよう。絵だけからでは判定は難しいが、もしもそれが言葉で机と説明されていれば、絵からの判定過程を省略して机という認識を得ることができる。アクセントはこれと同様な一種の名詞、あるいは注意書きであり、拍節の理解を経ずとも直接強拍の位置を教えてしまう。
もしも小節が、机や水の結晶のように、人間の認知的行為以前に完成している存在ならば、聴き手は人間の外で完成している小節をただ知覚するに過ぎず、音楽理論家は拍節の性質の根源を音の刺激を調べることによって追求すべきことになるだろう。これまでの音楽理論の誤りは、拍節を音楽の刺激の中に存在するものとみなし、拍節の本質を刺激の中に探し求めて来たことにあった。つまり規則的な刺激があって、それをただ知覚することによって拍節の認識が成立すると理解されてきたのである。私が音楽の認知に注目する理由はまさにここにある。音楽とは人間が認知して初めて音楽となるのであり、音楽の性質というのは、音楽を構成する音の性質ではなく、音楽を聴く人間の性質の反映なのである。
人間の性質の反映としての音楽
それでは「音楽を聴く人間の性質」とはいかなるものであるのか。近代の通常の音楽において、小節や拍といった拍節的構造は規則性を持つということが本質的な特徴であるとされてきた。では小節やビートは、なぜ規則的に生じるのだろうか?音楽の音自体が、それらの位置を自ら規則的にするのだろうか?もちろんそのようなことはあり得ない。もしもそれが物理的な物質であれば、例えば水の結晶を考えてみれば、水の分子が規則的に並ぶ原因になっているのは水の分子の物理化学的性質であると言えるし、どのような並び方をするかは水の分子の振る舞いを詳しく研究することによって理解できる。だが音楽においては、音の物理的性質をどれほど調べても、規則性の理由を知ることはできない。なぜならば、この規則性は作曲家によって音楽に与えられたものだからである。
実際、音楽の音は、作曲家や演奏家によって特定の位置に置かれるのである。ではなぜ彼らはそれを規則的に配置するのだろうか?それは聴き手がそう望むからだ。もちろんこの場合、作曲家や演奏家も聴き手の一員であり、聴き手なら同じような配置を望むであろうという期待に基づいて曲が作られている。聴き手が規則性を要求するのは、規則的である方が音楽の理解が容易になるからである。なぜ理解が容易となるかと言うと、規則的であれば予測ができるからである。予測とは、前もって次に来る「形」を知っていることだ。例えば階段を考えてみよう。もしも階段の段差の高さや奥行きが一段ごとに異なっていたら、我々はその階段を素早くリズミカルに上り下りすることはできず、一段ごとに測定を行う必要が生じる。我々が階段を難なく上り下りすることができるのは規則的だからである。音楽も同様である。我々は、音楽にこのような「形」を当てはめることで階段をリズミカルに上るかのごとく理解しているのだ。そして階段の段差は、素材が自ら規則的になったわけではない。ユーザーの要求に合わせて、人間である設計者や建築業者が規則的となるように作ったのである。
ここで重要な仮説を立てることができるだろう。それは、我々が音楽を、そこに我々が心の中に持っている何らかの認知的な枠組みを当てはめることによって聴いているのではないか、というものである。音楽が規則的であるのは、聴き手のこのような認知能力を前提とした、聴き手と作曲家や演奏家との間の相互作用の結果なのである。これは階段が規則的であることと全く同じなのだ。
音楽の中で最も規則的になろうとする部分は、この認知的な枠組みと最も関係の深い部分であろう。音楽の中で最も規則的になろうとする部分というのは、言うまでもなく拍節構造である。ゆえに、拍節構造はこの認知的な枠組みの性質をもっともよく反映していると考えられる。いやそれどころか、拍節構造とはこの認知的な枠組みそのものだと考えられるのである。このことについてさらに考えていこう。
第2節 認知のフレームワーク
スキーマ
先の議論で我々が推定した枠組みは、心理学や人工知能などの認知科学諸分野で提案されているフレームやスキーマなどと呼ばれる構造と極めて良く似ている。フレームあるいはスキーマとは、人間が外界の情報を処理する際に用いていると想定されている仮定されたデータ構造である。マーヴィン・ミンスキー(Marvin Minsky)はフレームを「居間に居るとか、子供の誕生パーティに行くとかいうような、形にはまった状況を表現するためのデータ構造である」と説明している。類似した概念が様々な分野で用いられているが、統一された理論があるわけでもなく、用語もばらばらである。人工知能研究に大きな影響を残したミンスキーがフレームという用語を用いたので人工知能分野ではフレームと呼ばれることが多い。また、特に時間軸に沿ったイベントを論じる際にはスクリプトという言葉も用いられた。一方で心理学では一般に、ギリシャ哲学やカントの用語に由来するスキーマ(シェマ)という用語が用いられる。言語学ではフィルモア(Charles J. Fillmore)によりフレームという用語が広まっている。フレームやスキーマと類似した構造はプログラミングでも用いられており、そこではオブジェクトを生み出す雛型がクラスとかタイプなどと呼ばれる。ロッシュ(Eleanor Rosch)はカテゴリーという用語を使って類似した問題を論じている。
この理論で私は、上記のような様々な領域において、共通した一般的構造がそれぞれの目的に合わせて異なった名称で論じられていると考え、その共通した構造をスキーマと総称することにする。ここで注意しておかねばならないことは、このスキーマという概念によって説明が試みられる対象は、カントが挙げているような、「三角形」、「5という数」、「犬」といった比較的単純なものから、バートレット(Frederic Barlett)によるような物語の構造といった膨大で複雑なものに至るまで、研究者によって多種多様であることである。しかしここでの議論においては、複雑な対象を考える必要は全くない。この議論でのスキーマの用い方は、三角形や数字の5を対象にする場合に非常に似ており、定規の目盛りのような構造を想像していただければ十分である。
スキーマの特徴
ラメルハートとオートニー(1977)によれば、スキーマは4つの主要な特徴を持っている。
(1)スキーマは変数を持つ。
(2)スキーマは別のスキーマの中に埋め込むことができる。
(3)スキーマは抽象化の様々なレベルで一般的な概念を表現する。
(4)スキーマは、定義ではなく知識を表現する。
ここで変数というのは様々な抽象度を持ったデータ構造のことである。これらの特徴を人間の顔の認知に用いられると想定されるスキーマを例に用いて説明しよう。顔のスキーマには目とか鼻といった顔を構成する部品に対応する変数のデータを収める場所が配置されていると想定される。それぞれの変数は単なるデータではなく、それぞれが目のスキーマや鼻のスキーマになっている。さらにその目のスキーマは、その中に睫毛だとか瞳だとかを表現するより具体的で小さなスキーマを変数として含んでおり、それらもまたスキーマである。もしも顕微鏡などの道具を使うならば、これをどんどん細分化していくことも不可能ではないだろうが、それはもはや人間が人の顔を理解する際に用いるデータではないのでそこまで考える必要はない。一方で顔のスキーマは、より大きなレベルの人体のスキーマの一部分である。
このようにしてスキーマの階層性は、人間の通常用いるようなレベルを中心として上へ下へと広がって行く。それは大きなレベルほど抽象的であろうし、細かいレベルではより具体的なものである。このような構造によって我々は顔の抽象的特徴だけではなく個別的な特徴を処理可能なデータ構造にまとめていると考えられる。
顔と目や鼻は、全体と部分の関係にある。このとき、顔のスキーマと目や鼻のスキーマは、似たような機能を持っているが、内容的にはそれぞれ全く別のスキーマである。このような関係は「全体と部分」の関係ということができるだろう。スキーマの関係にはこのような「全体と部分」関係の他に、例えば自動車のスキーマと乗用車のスキーマの関係のような「~の一種である」という関係がある。後者の関係の場合、より漠然とした大雑把な自動車のスキーマに、乗用車を表現するためのサブスキーマを入れ子状に加えることによってより具体的な乗用車のスキーマが作られていると考えることができる。このようなとき、乗用車のスキーマは自動車のスキーマに対する子孫のスキーマであり、自動車のスキーマの特徴を継承していると言われる。
スキーマは、データを読み取る際のフォーマットであるとともに、プログラミングで典型的に見られるように何かを生み出す際の雛形でもありうる。例えば、人の顔を描く時、人はしばしばスキーマを呼び起こすための必要最低限の描写で済ませることができる。顔のスキーマは、顔の大雑把な表現や理解を可能にする。プログラミングでは、先ほど述べた継承の仕組みを利用して、親スキーマの特徴を受け継ぎつつも内容の付け加わった子スキーマを作り、情報の節約や整理のために活用している。
音楽の拍節構造は人間の持つ音楽理解のためのスキーマである
ここまでスキーマの性質をなるべく一般的な観点から見てきたが、音楽の拍節構造はこのようなスキーマの特徴をよく備えている。スキーマが変数を持つという特徴は、拍節構造が各部分に音楽的イベントを持つことによく似ている。例えば、1つの音だけを持つ小節を考えてみよう。小節をスキーマとみなすと、それは変数を1つ持つスキーマであり、繰り返せばビートになる。このイベントはさらに音色や音高などの情報を持つであろうが、拍節においてはまずはその位置が重要である。この音符を2つの音符に等分してみよう。これは、小節のスキーマが2つのサブスキーマによって構成されているのと同じであり、2拍子に他ならない。この2つの音符をさらに等分してみよう。2分割と3分割の2通りのパターンを考えてみれば、ここで我々が得るのは4拍子と6拍子である。この2つの拍子はそれぞれ、2拍子を親とする子スキーマであり2拍子の特徴を継承している。つまり、4拍子の大雑把な理解は2拍子ということである。
拍子や拍のレベルは人間が拍節構造を最もはっきりと感じるレベル付近に設定されることが多い。これはロッシュのカテゴリー論における基本レベル(basic level)の考え方と合致する。
以上のことより、音楽の拍節とは人間の持つスキーマそのもの、あるいは諸作品におけるそのスキーマの反映である、と結論付けることができる。つまり、音楽の拍節についての議論とは、人間の持つスキーマについての議論に他ならないということである。
第2章 イベントと時間
第1章で導入したスキーマは、どのようにして音楽的なイベントを捉えるのだろうか?それはイベントの時間的な位置の把握に基づくのである。だから拍子とは、複数のイベントの位置によって構成される一種の図形に似ている。
第1節 イベントの開始位置とアクセント
イベントの開始の位置
メトロノームの音に合わせて演奏する時、演奏者は自分の発する音の開始の位置を、メトロノームの音が示すタイミングに合わせようとする。それは彼の発する音がレガートであってもスタッカートであっても変わらない。これは、我々の持っている認知的な枠組みが、音楽的なイベントをその先頭の時間的な位置によって捉えているということだ。しかしこの位置というのは、単に物理的な刺激の始まる点ではない。この位置とは、そこからイベントが開始したと我々が感じる点のことである。例えば下の図2-1.1のaのように、極めて音量の小さな音が徐々に音量を増大させて再びゆっくりと減衰していくようなイベントを考えてみよう。物理的な測定を行えば、そのイベントの開始の位置を決められるかもしれないが、我々はこれをタイミングを合わせられるようなイベントとして捉えることができない。あるイベントの音量の変化がこのような緩やかな曲線を描く場合、我々はそのイベントを「リズム的」に捉えることができないのだ。これは画像における「エッジ」の検出とよく似ている。色彩を捉える際に我々は、なだらかなグラデーションにおいてはどこで色が変わったのかを決めることができない。このようなエッジを検出するためには、図2-1.1のbのような音量変化が必要となる。

我々が通常扱う音楽的イベントはほとんどがこのbのような曲線を描くはずだ。このような鋭い音量の増大があれば、人間は開始の位置を把握することができる。よって本論の立場では、リズム的現象を論じる際に一般に用いられているIOI、すなわち始点間距離(inter-onset-interval)を「人間が感じる」という条件を付けずに用いることはできない。
一方で人間は、イベントの終わりの位置をはっきり捉えることができない、もしくはあまり重視していない。例えば、発せられる音がレガートであるかスタッカートであるかの違いは、音の刺激としてはイベントの持続時間の違い、つまり終わりの位置の違いである。しかしこの違いは我々のイベントのタイミングについてのリズム的な感覚に何の影響も与えておらず、ほとんど音色の違いのようなものとして、つまりイベントの属性の違いとして解釈される。
聴き手にとって、あるイベントの終わる位置がはっきりと分かる場合というのは、音が突然消えるような場合であるが、それは実際には無音というイベントの開始を感じていると捉えるべきである。
アクセント
しばしば「アクセントを付ける」という言い方が一般になされるが、これには注意が必要である。というのも、アクセントはイベントや物体ではないのだから、この「付ける」という言葉は、物を貼り付けるようなものとして理解してはならないからである。アクセントというのはイベントに付随する属性であり、アクセントを付けるというのはイベントの持つ何らかの値を変動させることを意味している。
アクセントとはイベントのどこに付くのであろうか?音量が一定で持続するようなイベントであっても、そのイベントの持続全体にアクセントが付いているとは理解されない。アクセントの付けられる位置は、イベントの開始の位置と同一である。つまりイベントも、その属性であるアクセントも、開始の位置によって理解されるのである。
「アクセントがない」という形容には注意が必要である。もちろんアクセントがないイベントは無音ということではない。通常「アクセントを持つ」とか「強いアクセント」と言われる状態というのは、他のイベントの持つアクセントより強いとか、目立つということを意味している。逆に「アクセントがない」というのは、そのイベントが持つアクセントが他のイベントの持つアクセントより弱いとか、目立たないということを意味している。
だが、アクセントを人間の注意力の代理として用いるならば、「アクセントが無い」という言い方は成立するかもしれない。しかしこれは、人間の注意力が刺激の中に存在するという極めて倒錯した考え方につながりかねない注意を要する考え方である。実際にはアクセントを感じるのは人間であり、物理刺激の中には人間がアクセントを感じる解釈可能性だけが存在している。アクセントが特定の位置にあると解釈しているのは人間であり、それらの差異を意味のある違いと認めて、グループ分けしたり、注意を向けたりするのも人間である。これらのことから、アクセントの問題というのは、人間が解釈するイベントの開始点とイベントの種類の違いの問題というのとほとんど同じだということが分かるだろう。
アクセントには「強さ」の違いというもう1つの別の側面がある。アクセントの「強さ」に違いを与えると、同一のイベントに差異を与えることができる。つまり、強さの違いが無ければ同一であったようなイベントが、複数の種類に分かれるということである。2種類の強さのアクセントを用いるならば、イベントは2つの種類に分かれるだろう。一方でその意味で言えば、同じ強さのアクセントが付けられたイベントは「同一のイベント」ということになる。これは音色などの違いとよく似た効果をもたらす。アクセントの違いを与えることは、イベントの種類の違いを作ることとほとんど同じなのだ。
ところがすでに指摘したように、アクセントという概念は、注意深く用いないと、あたかも物質のように、刺激の中に実在するかのように扱われてしまう。最初に注意したように、それは「値」の違いでしかないのだが、人間によるその違いの識別やその位置の理解が、まるでアクセントという物体が刺激の特定の場所に置かれているかのような錯覚をもたらすのである。だからその幻の物体は、人間の注意が向けられなくなるとどこかに消え去ったりするし、あるいは逆に、人間の識別能力を遥かに超えた微細な等級を持つことができることになったりするのである。図1-1.3で6段階もの区別がなされていたことを思い出していただきたい。実際には人間は6段階のアクセントの違いを識別できないだろう。つまりこれは、実際のアクセントの違いを意味しているのではなく、拍節的な階層構造をアクセントの違いで表現しているのに過ぎないのである。それはサーモグラフィーが実際の温度とは無関係の色を用いて温度の違いを表示しているのとよく似ている。
こうした考え方は、人間の反応を、先回りしてそれの原因となった刺激の中にすでに存在するかのように捉えることによるよくある誤りである。悲しみや喜びが、音楽の中にすでに込められているという考え方は古くから存在したものであった。アクセントや拍節も、同じように人間の外へと引きずり出され、客観的に完成されたものを人間がただ知覚するだけであるかのように捉えられるのである。
以上アクセント概念やそれにまつわる注意事項や混乱について述べて来たが、アクセントに関するこのような誤解は、実は便利なものとして上手く利用されて来たともいえる。アクセントという概念は、人間の反応を人間の外部に実体化させるための装置となる。アクセントを用いれば、「人間がイベントの開始の点を感じる」と言う代わりに、「イベントがアクセントを持つ」と言えば済むのであり、そうしたアクセントの中の1つに人間が注意を向けている状態を「イベントが強いアクセントを持つ」と言えば済むのである。そして、音の強さによってイベントが2種類にカテゴライズされている状態は、「強いアクセントと弱いアクセントが交代している」と言えば済むというわけである。この場合にはアクセントとは、客観的な刺激の強さのことなどではなく、そのような刺激に対する人間の反応までを加味した上で、改めて刺激の側に実在するものであるかのように差し戻した概念なのである。
第2節 拍子の形成
アクセントと拍子
アクセントがあるということ自体や、アクセントを単に知覚することだけでは、拍子のような構造は生じない。それは、個々のアクセントが、それぞれある一点に存在する孤立したものでしかないからである。これは、アクセントをいくつか集めたり、その中の1つのアクセントを強くしたとしても全く変わらない。それだけでは、それぞれが孤立したアクセントであることに何の変わりもないからである。ではアクセントが規則的であったらどうだろうか?それでもやはり、それだけでは拍子は生じない。というのも、孤立しているはずのアクセントが、ただ規則的に並んでいるというだけで繋がったり関連しあったりするはずがないからである。
では、それらのアクセントの間に拍子を生み出すものは何か?そのためには人間の関与が必要である。つまり拍子を生み出すのは人間の持つスキーマである。人間は、幾つかのアクセントを、例えばそれらを2拍子をなすものであるとみなすことによって2拍子にしているのである。もちろんこれは、それらのアクセントが2拍子のスキーマにとって受け入れやすい場合にのみ可能である。2拍子のスキーマにとって受け入れ難い場合は、別のスキーマよって受け入れられるか、あるいは理解困難ということになる。作曲家や演奏家は、2拍子として理解してもらいたい場合には、2拍子のスキーマにとって受け入れやすくなるように音を配置するであろう。しかしどれほど受け入れやすい音の配置であろうと、人間の関与なしに音は拍子にはならないのである。音の配置などの刺激自体の違いは、聴き手によってある解釈をされる可能性を持つに過ぎない。
ところですでに、アクセントがイベントの開始の点およびイベントの種類の違いと同等であると論じた。よって拍子のスキーマとは、イベントの位置関係を認識するものであると考えていいだろう。アクセントの差異、あるいはイベントの種類の違いの認識は、この位置関係の様々なタイプを識別するための情報となる。この理論では拍子のスキーマを、イベントの位置関係によって作られる一種の「形」を理解するための構造であると考える。
スキーマとはギリシャ語で「形」を意味するσχῆμα(skhêma)に由来する言葉である。アリストクセノスは、音や踊りのステップと、そうした時間上のイベントによって作られる時間区分との関係を、「形を取ることのできるもの」と「形」との関係と比較して論じている。アリストクセノスのリズム論においてリズムとは、このような形のうちの特に好ましいもののことであった。そして形を取ることのできるもの、つまりリズムを持つことができるものとしてまず考えられたのは、言葉と音と踊りのステップであった。その際リズムの種類は、脚という形式で現れる。この脚という形式は、その後音楽の拍子の考え方を、少なくとも18世紀までは支配していた。これはもちろん、時間の長短に基づくものである。この考え方に大きな変化をもたらしたのが、拍子を形ではなくアクセントによって理解するやり方であった。
アクセントと拍子の関係についての誤解
アクセントの差異そのものは拍子ではないが、アクセントの差異が聴き手に特定の拍節構造を感じるように促すことができることは確かである。その意味で、アクセントやそれらの差異は一種の記号である。ところが、このことから多くの理論家は、刺激にアクセントが付いていること自体を拍節の存在と同一視してしまう。すでに述べたように、人間の外にある刺激そのものは拍節の可能性に過ぎないのだが、その刺激が人間に拍節構造の解釈を促すので、まるで刺激それ自体が拍節であるように錯覚してしまうのである。
アクセントの人間の外にある刺激の中での存在を、そのまま拍節の存在とみなすことを否定しなくてはならない。アクセントの差異は、聴き手がスキーマを当てはめる際に参考とする情報の1つに過ぎないのである。楽曲に存在する刺激の様々な違いは、拍節的解釈の可能性の様々な様態である。楽曲の拍節とは客観的に存在するものではない。本研究は、楽曲の客観的な拍節を調べようとしているのではなく、聴き手による解釈の可能性を調べているのである。本論の研究対象は、様々な対象に対して、聴き手がどのような解釈をすることができるのか、という、聴き手の側の持つ道具箱の内容である。
拍子の形成に関するイエストンの誤謬
イエストン(Maury Yeston)は現代アメリカの音楽理論に大きな影響を残した理論家であり、彼の拍節理論は、後のGTTM理論や拍節構造や、クレブス(Harald Krebs)のシンコペーションやヘミオラの議論の基礎となっている。しかし彼の拍子概念には大きな欠陥があり、今のうちに言及しておく必要があるだろう。
彼の理論では、拍子というものは複数のビート列の間の相互作用によって作られると主張されている。なるほど確かに例えば2/4拍子は、下の図2-2.1に示したように、4分音符の規則的な連続と、2分音符の規則的な連続によって構成されているように思える。4分音符の連続だけでは、拍子のグループを生み出す要素が含まれないので拍子にはならないであろうし、2分音符の連続だけでは分割のきっかけがない。そう考えると、確かに拍子は2つの「層」の相互作用において生じているように思えてしまう。だがこの考え方には根本的な誤りが含まれている。それは、初期状態として、4分音符の層と、2分音符の層が、独立して存在している状態を考えていることである。もしもこの2つの層が独立しているならば、両者は互いに無関係なのだから、この2つの層のタイミングが合うことは無いはずであろう。ところが2/4拍子の小節の連続においては、2分音符の連続は4分音符の連続と1つおきに同じ位置を占めている。2つの層がそのような関係になるためには、どちらか一方が他方から作られたと考える他はあり得ない。さらに言えば、パルス列が最初から存在することなどもあり得ない。パルス列は、何らかの周期の決定を経て、スタート地点から1つ1つ打たれるものだからである。

すなわちイエストンは、結果として生じることになる規則性を、誤って出発点としてしまったことになる。これはちょうど、人間の足跡を、右足の足跡の層と、左足の足跡の層との合成によって作られていると主張するようなものであろう。このような考え方は、分析のためのテクニックとしては利用可能かもしれないが、拍子の本質とは全く異なる誤った考え方である。
第3章 スキーマによる理解
第1節 ラメルハート&オートニー(1977)による理解のモデル
聴き手はスキーマを用いて、イベントをどのように理解するのであろうか?この点について、ラメルハートとオートニーは、次のような明確な定式を与えている。
『その状況が、そのスキーマが表す概念のインスタンスとして解釈されうるとき、我々はそれをあるスキーマが状況を「説明している」と言う。』
『情報を十分説明するように思えるスキーマのセットを見つけたならば、その人はその状況を「理解した」と言われる。』
これを、極めて簡単な階段のスキーマを用いて説明しよう。ここでは単純に、まっすぐ進むだけの階段を考えてみる。その時、階段のスキーマの種類は、1段ごとの高さと奥行きの違いによってのみ区別される。それ以上の詳細な情報は、階段の上り下りとはあまり関係のない内容である。つまり階段のスキーマは、高さと奥行きのパラメータの違いだけで表現できる。歩行者がある階段をスムーズに上り下りすることができる時には、当然歩行者はその階段を理解している状態にある。
ラメルハートたちの考え方に従えば、ある現実の階段の特徴が説明されるというのは、その階段が特定の高さと奥行きを持った階段のスキーマのインスタンスであると解釈されることである。歩行者は、その階段を説明するようなスキーマを頭の中から探してくることができれば、その階段を理解したことになるであろう。そして歩行者は、このような適合するスキーマを、奥行きと高さのパラメータを変えるだけで簡単に用意することができる。パラメータを変えるだけであらゆる階段に対応するスキーマを得ることができるということは重要である。というのは、歩行者は無限個の階段のスキーマを持っているわけにはいかないのであるから、適切なスキーマを少ない手続きと少ない記憶容量によって得るための仕組みが必ず必要になるからである。この点についてはすぐ後で論じられることになる。
顔のスキーマで考えれば、ある視覚刺激の配置を顔のスキーマのインスタンスであると解釈することが、その配置を顔であると理解することである。そしてこの理解が可能なのは、見る人が顔のスキーマをすでに所有しているからであるし、そのスキーマは、実際の顔の配置の多様性に対応できるように、伸び縮みできるような性質を持っていることだろう。この伸縮には限度があるだろうし、人間の通常の顔は、そのような伸縮によってスキーマを容易に得られる範囲に収まっているはずである。この限度がどのようにして決まるかをここで論じることは難しいが、スキーマにこのような柔軟性があるということは重要である。というのは、例えばある手書きの図形を三角形であると認める時、それは見る人が、手書きであることによる図形の歪みなどを無視して、その視覚刺激による配置を三角形のスキーマに押し込むことができるということを意味しているからである。これは対象の誤解の原因にもなりうるが、必要とするスキーマの種類を節約する効果を持つはずである。
さて、これを音楽を対象とする場合に当てはめて考えてみよう。ある構造を持つ音楽的な対象があると想定する。これがあるスキーマのインスタンスとして解釈されうる時、このスキーマは、この音楽的対象を説明していると言える。聴き手は、ある対象について、それを説明するスキーマを心の中のストックから見つけ出せたときに、その対象を理解したことになる。このとき聴き手は音楽的な様々な形のそれぞれに対応するスキーマを別々に持っているのではなく、階段の例で述べたように、何か単純な仕組みでそれぞれの形に対応するスキーマを生成することができるはずである。なぜならば、もしもバラバラにスキーマを持っていたならば、聴き手は極めて多くの種類のスキーマを持っていなくては、多様な音楽を理解することができないことになるからであるし、適切なスキーマを見つけ出すことも容易ではなくなるだろうからである。
ラメルハートとオートニーやミンスキーの想定しているスキーマ(あるいはフレーム)は、私の考えるそれとは少し異なり、より固定的で概念的なものであるように思われる。彼らは、概念やイベントに対して、1つのスキーマが常に変わらず対応するように考えている。だが音楽構造では、ある1つの典型的な形だけを考えるよりも、少しずつ異なった連続的な様々な構造を考える必要がある。そして実は、レストランとか子供の誕生会といった彼らが考えていたスキーマにも、少しずつ異なるスキーマを考えることができるのではないだろうか。しかしそうした連続的なスキーマを考えるためには、レストランや子供の誕生会は、少し複雑すぎる例であろう。ここに、音楽構造を用いてスキーマについて考察する意義があるように思われる。音楽はこの研究のために、適度に単純な対象である。
第2節 グループ化の原理
グルーピングの役割
レーダールとジャッケンドフによるGTTM理論(Generative Theory of Tonal Music)は、グルーピングを、人間の認知の基本的な作用であるとしている。
『グルーピングの過程は、人間の認知の多くの領域で共通である。要素の連続や、イベントの連続に直面すると、人は自発的に(無意識に)、諸要素あるいは諸イベントを、ある種のグループへと分ける、あるいは「チャンク化」する。この作用を彼が行う容易さと困難は、インプットの内的な組織が、どのくらいうまく、グルーピングを作るための彼の内的な、無意識の原理とマッチしているかに依存している。』
私はこの点でGTTMと同意見である。しかしGTTMではこのような音楽のグルーピングをモデル化するに際して、音楽のグルーピングを考えるのではなく、主として視覚的対象の性質に基づいた一般的なグルーピング概念を音楽に当てはめることで議論を済ましてしまっており、音楽におけるグループの本質について論じることを回避してしまっている。このため、音楽において諸イベントがグループ化することは認めるとしても、どのような仕組みによって音のグループ化が起こるかは不問とされ、ただ音楽的諸イベントの持つ様々な特徴からグループの境界の位置を決定するルールを構築するという議論に向かってしまう。これは、GTTMが結局のところは音楽の人間的理解を目指すことよりも、機械によって自動的に処理するシステムの構築を優先しているからである。つまりGTTM理論はその本質が、コンピューターを用いた人工知能の研究にあり、そのため、結局のところGTTMのグルーピングは、人間の判断するグルーピングと同一である必要すらないのである。
本研究は音楽の実践的な理論を目指しているのであるから、GTTMとは別の道を取るべきであろう。本論では自動的に機械で判定できるようなルールのシステムの構築は目指さない。本論が目指すものは、人間が音のグループを作る仕組みの解明である。
グループ化の原理
ここで1つの原理を提示しよう。それは「諸音はそれ自身ではグループにはならず、聴き手の持つスキーマがそれらの音をグループにしている」というものである。音という物理的な存在が、自らグループを作ったりしないことは自明である。諸イベントの互いの関係は、人間による解釈の可能性を変化させるだけに過ぎない。グループを作るのは聴き手自身の認知である。
このことを、先に述べたラメルハート達による定式化と合わせて表現すると次のようになるだろう。
グループは、聴き手が諸イベントを聴き手の持つスキーマに当てはめることによって生じる。だからグループとは、スキーマのインスタンスであるとみなすことができる。この時、このスキーマはこのグループを「説明している」と言えることになる。そしてそのグループを十分説明するように思えるスキーマのセットを見つけたならば、その人はそのグループを「理解した」と言える。逆に言えば、聴き手は適切なスキーマを見つけられない諸イベントをグループとして理解することはできない。
すなわち音楽におけるグループは、スキーマのみに基づく、ということである。本論ではこれを「グループ化の原理」と呼ぼうと思う。あるスキーマは、インスタンスとしてのグループを一義的に決定する。しかしある1つの音楽的なグループはそのよって立つ構造の解釈の可能性に応じて、複数のスキーマによって理解される可能性がある。これは普通はグループという表現方法が、それだけではスキーマによって表現される構造を完全には記述できないからである。これは物体と影の関係に似ているかもしれない。物体は決まった影を落とすが、影から推測される物体には複数の可能性がある。ただし影は1つの輪郭しか持たないが、スキーマによって作られるグループは入れ子状の階層構造を持っている。
第3節 継承関係に基づくスキーマ・システム
さて、グループ化の原理から、スキーマに求められるある性質が明らかになる。これを疑問に答える形で論じようと思う。
疑問1:
グループが複雑化した拍節のスキーマに基づくならば、複雑なグループにおいては、複雑な拍節があるだけであって、聴き手が通常音楽で経験するような簡単な拍節は分からなくなってしまうのではないだろうか?しかし音楽では、複雑なパッセージにおいても、穏やかで単純なグループにおいても、単純な拍節が明確に感じられる。これは矛盾ではないだろうか?
疑問2:
グループの形ごとにそれをインスタンスとするようなスキーマがあるとするならば、聴き手は音楽の様々なグループを理解するために膨大な量のスキーマをあらかじめ持っていなくてはならないことになるではないか?それは脳の記憶容量の無駄遣いではないだろうか?
疑問3:
どれほど多くのスキーマが用意できたとしても、それらによって対応できないグループが必ず存在するのではないだろうか?もしも対応できる範囲が決まってるとするならば、一体どのようにして、対応する範囲が決まるのだろうか?
疑問4:
仮に、そのような膨大なスキーマをあらかじめ持っていることができたとしても、どうやってその都度、適切なスキーマを短時間で探し出すことができるのだろうか?
疑問1に対しての私の答えは、聴き手が音楽の複雑なグループを、大雑把には単純な拍節であるようなものとして理解している、というものである。これは極めて重要なことである。例えば、大変にテンポが速いのに、非常に細かい動きを持った楽曲があるとした時、聴き手の理解がその速度に追いつかないということがしばしばありうる。そのような時、その細部に至るまで理解しないと楽曲が理解できないということでは、聴き手はほとんどの音楽を理解することができなくなってしまうであろう。よって、聴き手は、適度に省略的に、大まかな理解で満足することができなくてはならない。
そこでこのように考えよう。複雑なグループは、単純なグループの修飾として理解できるし、単純なグループもまたさらに、もっと単純な拍子の修飾として理解することができる。12拍子は4拍子の修飾として、さらに4拍子は2拍子の修飾として理解することができるのである。
ここでスキーマは、オブジェクト指向プログラミングで用いられる「クラス」とほとんど同じ性質を持っていると考えられる。クラスは、その親にあたるスーパークラスから性質を継承し、より細かい性質を付加されたものである。これと同じように、音楽のグループのためのスキーマは、性質を継承する関係にある。そして、必要な理解の深度に応じて、大雑把なスキーマとして理解したり、詳細なスキーマとして理解したりを使い分けることができるのであろう。ただし、本論がここで考える継承関係は、音楽の「形」を理解するスキーマとしての関係に限定される。よって、スーパースキーマが「音楽一般」などといったさらに抽象的な概念に遡ることは考えない。
疑問2については、ラメルハート&オートニーが同様の問題に言及している。
もし理解が、入力を説明するためのスキーマやスキーマのセットが使われることによって達成されるとするならば、考えうるあらゆる入力のためのスキーマが存在するという不合理な結論をどうやって退けるのだろうか?
If comprehension is achieved by utilizing a schema or set of schemata to account for the input, how is the absurd conclusion that there exists a schema for every conceivable input to be avoided?
彼らの回答は、単純なスキーマを組み合わせることによって全体の理解を得られるだろう、というものである。しかし彼らが、そのような組み合わせが生じる場合の例として挙げている状況は「ある女の子がアイスクリーム売りの声を聴く」という、かなり複雑な状況であって、ここでの議論には相応しくない。本論では、疑問1に答える際に述べた継承関係に基づく形の理解のためのスキーマを用いて、このことをもう少し単純に説明することができる。
例えば、4拍子が2拍子の修飾として理解できるならば、聴き手は4拍子のスキーマと2拍子のスキーマを、2拍子のスキーマから4拍子のスキーマが生成されるような1つのシステムとして理解することができるだろう。このシステムは、パラメータを変えることによって6拍子を生成したり、さらに12拍子を生成したりすることができるようになるはずである。このように考えれば、聴き手はスキーマをそれぞれ個別に用意していると考える必要はなくなる。このようなシステムによって、ふさわしいスキーマをその都度生成することができるからである。
このようなシステムを想定すれば、疑問3と疑問4にも満足のいく回答を与えることができる。聴き手は、このようなシステムによってスキーマを容易に生成できる範囲の対象ならば、容易に理解することができると考えられる。よって、スキーマの生成が困難な対象、もしくは容易に生成できるスキーマによっては捉えられない対象は、不可能ではないにせよ、理解もその分だけ困難となるだろう。そして、このシステムにおいては、諸スキーマはバラバラに存在するのではなく、1つの樹状の系列にまとめられているので、適切なスキーマを選び出すことも容易になる。
私は、音楽の理解に限らず、スキーマを用いた理解が満足に機能するためには、このようなシステムを想定する必要があると考えている。そして、このようなシステムを持つものの中で、音楽の理解のためのスキーマ・システムが、おそらく最も単純で規則的なものであろう。その理由の1つは、音楽をほとんど幾何学的図形の理解のようなものとして扱えることによる。これによって「意味」のような複雑な問題を扱わなくて済む。また、幾何学的図形のようなものと述べたが、音楽の時間区分は一次元的な情報であり、図形というよりもむしろさらに数直線のような対象に近いものである。だから音楽では、図形に必要となる複雑な2次元的な位置関係の表現を扱わなくてもいいのである。このような理由から、音楽のリズム理論は、このようなスキーマ・システムの議論の出発点として手頃なものであると言ってよかろう。
第4章 拍節のスキーマ・システム
第1節 基本的な拍節構造
3つの基本的なメタスキーマ
第1章で、拍節構造は、音楽的対象の中に存在するものではなく、音楽を理解する聴き手が音楽的対象に与えるものであることを指摘した。その時、音楽的対象の持つ配置は、聴き手によって拍節構造であると解釈される可能性を持つに過ぎない。このような聴き手による解釈は、この章で説明するような拍節の認知スキーマに基づいて行われる
第2章で、拍節の本質がイベントの時間的配置にあることを論じた。アクセントは配置を人によく示すための簡便な手段ではあるが、拍節の本質はアクセントではなくそれによって示される配置の方にある。すでに古代ギリシャでは、このような配置や、そのうちの特に良きものについて、形(スケーマ skhēma)とか、リュトモス(rhythmos)と呼んでいた。しかし古代ギリシャ人が良きものと考えた形と、今日の音楽のそれとは明らかに異なっている。そこで本章では、経験に基づいて今日の音楽における良き形を明らかにせねばならない。
すでに3章で述べたように、聴き手がある刺激を前にした際に、その刺激を理解するというのは、その刺激がインスタンスであるようなスキーマを見つけ出すことである。このような理解のためのスキーマを限られた能力の中で簡単に探し出してくるためには、諸スキーマが、何らかのシステマティックな仕組みで関係付けられており、必要に応じて生成されるようなものである必要がある。本論がここで想定する仕組みは、継承関係に基づく系統関係である。
すなわち、小節のスキーマを出発点として、2分割するならば2拍子が得られるし、3分割するならば3拍子が得られる。この時、2拍子と3拍子は、それぞれ小節の一種であり、小節の性質を継承している。2分割と3分割の違いは、同じ仕組みにおけるパラメーターの違いでしかない。それらをさらに2分割、3分割するならば、4拍子や6拍子や9拍子が生成されるだろう。このようにして、2拍子、3拍子、4拍子、6拍子、9拍子を含む諸スキーマの、1つのシステムを考えることができる。聴き手はこのシステムの系統関係を辿ることによって、対象にぴったりなスキーマを選ぶことができるだろう。そして、短い手数の基本的な手続きによって得られるスキーマは、ほとんど最初から用意しているスキーマと同じように扱うことができるだろう。すなわち聴き手は、諸スキーマの全てを保持していると言うよりも、スキーマを生成する仕組みを持っているのであろう。このようにすれば聴き手は大量のスキーマをあらかじめ用意しておく必要がなくなり、記憶の容量を圧迫するという問題を回避することができる。
このような基本的な手続きとは、スキーマを生成するためのメタスキーマである。音楽の拍節構造を得るためには、以下のような3つのメタスキーマが必要となる。
1、等時性
2、分割
3、単純比
等時性は、等しい間隔による連続を把握するためのスキーマを生成する。このスキーマは音楽において最も基本的なスキーマであるが、これだけでは1つのビート列しか理解できない。
そこで2つ目の分割のメタスキーマが必要となる。これは実は、第1章第2節第2項で述べた「(2)スキーマは別のスキーマをその中に埋め込んだり、逆に埋め込まれたりできる。」というスキーマの性質そのものに由来している。埋め込まれるスキーマはそれを受け入れるスキーマより必ず小さいのであるから、1つ目のメタスキーマである等時性によって、ビートの階層性が生じる。
ところで、分割によって得られたサブフレームが等時性を満たすためには、フレームを単に等分すればように思われるが、等分というのは実は容易ではない。ある長さの半分や、3分の1の長さを求めるのはかなり面倒である。それが時間であればなおさら、等分するような長さを知ることは困難となる。
それゆえ、人が比率関係に関するメタスキーマをあらかじめ持っていると考える必要がある。日常的な体験を振り返ってみると、長さに関して2倍や3倍はおよそ判断できるが、5倍や7倍といった関係を感じることはかなり難しい。こうしたことから、2倍や3倍といった単純な比率のメタスキーマであるほど運用が容易であり、対象の把握が容易であると考えられる。この理論では基本的に2倍と3倍、およびその組み合わせのみを単純比と認める。
もちろん、この比率というのは対象が正確にこの比率を持っていなくてはならないということではない。聴き手は対象を大雑把に、こうした比率を持っているものとして理解することができる。単純な比率と、実際の対象の間のズレは、歪みとして認識される。
歪みとは、何らかの規則的なものとの比較によって理解されるものであろう。つまり歪みとは規則的なもののためのスキーマの修飾によって理解されると考えることができる。そしてこの際の、正確な比率との微妙なズレは、おそらく何らかの印象の違いとして感じられることになるだろう。本論はここでそのような繊細な問題を扱うつもりはないが、例えば音楽における「グルーヴ感」といった感覚は、このようなズレにともなう印象と深く関わっていると考えられる。
書き換え規則による時間区分列の集合の定義
これら3つのメタスキーマから作られるスキーマの全体の集合は、形式言語の記号列の集合の定義のやり方に倣って、次の図4-1.1のような書き換え規則によって表現することができる。ここで右辺の縦棒は、2分割か3分割が任意に選択できることを意味している。ただしこの書き換え規則は分割の比率のみを表現するものとする。すなわち左辺の4分音符は任意の時間区分を意味することとし、それに応じて右辺の8分音符も、左辺の2等分や3等分の長さを表すこととする。よって図4-1.1はその次の図4-1.2と等価である。伝統的にはこの書き換えの出発点は全音符、すなわちセミブレヴィスであった。

セミブレヴィスを出発点として、この書き換え規則を任意回数任意の位置に適用することによって、標準的な拍節構造を全て生成することができる。これは時間区分を表現する記号列あるいは時間区分列の集合的な定義である。これによって、可能なすべての標準的な拍節構造を生成する文法を定義したということになる。ただしもちろん、この書き換え規則によって得られる形の全てが、同様の頻度で用いられるということではない。聴き手にとっては、単純で同じ形を繰り返した形である方が理解が容易であることは明らかである。なお、用語の通常の用法における「拍子」とは、上記のような様々な可能な形のうちで、比較的典型的な単純な小節の分割のパターンを示したものであると言える。この意味での拍子は、音楽の実際の細かな音符のあり方やその変化に関わらずに、一定の基準を示すものとして用いられる。本論の観点から言えばこのような拍子を示すことは、親となるスキーマを記号で明示することによって理解を助けたり誘導したりしていることになる。
伝統的な音符のシステム
伝統的な記譜法における音符のシステムは、それを使うと意識せずとも上記の3つのメタスキーマを自動的に満たしてくれるように作られている。すなわち、同じ音符を使うだけで等時性が実現でき、ある音符をより細かい複数の音符で置き換えることができ、そして音符の種類は互いに単純な比の関係によって定義されている。それは数学の演算記号や式の変形のようなものである。単に記号の操作を覚えるだけで複雑な計算が、そこで何をしているのか意識せずとも処理できてしまう。音楽家はこのような音符を用いる際に、様々な長さの関係がありうる中で、等時的な区分列だけを選択し、単純な比率に従った分割だけを用いるように導かれているということを全く意識していない。伝統的な音符のシステムの発展は、人間の認知の仕組みを音符の記号のシステムへと落とし込むことであったと言っても過言ではあるまい。というのも、もしも人間の認知の仕組みに反したものであったならば、音符のシステムがこれほど普及することは難しかったであろうからである。
ヘミオラ
上記の書き換え規則における選択を、どちらかに限定せず両方同時に行うとヘミオラの構造が得られる。つまりヘミオラは異なった分割が並存することである。ただし、大抵どちらかの分割が優位となり、劣位な分割は不規則なシンコペーションのような感覚を与えることになる。
拍節の階層性は分割に基づくので、下の階層というのは、基本的には、上の枠ごとに分断されている。そのためそれぞれ改めて分割を開始するという感覚を与える。これは、本論が拍節をグループと考えることとも一致している。しかしヘミオラや長い連符などの場合に見られるように、同時に2通りの分割を感じている場合には、小さいレベルのビート列のグループが、大きいビートの範囲を超えて感じられる場合も考えられる。
第2節 不等分割を含む拍節構造—準拍子
不等分割に基づく準拍子
単純比のメタスキーマの箇所では、結果が等分になる分割方法だけを扱った。しかし、分割の単位が比率によるのであるならば、分割はかならずしも全体を等分するように行われなくてもいいはずである。例えば、付点2分音符と2分音符の比率は3:2である。これを単純な比に含めれば、付点2分音符を、そこから2分音符を分け取ることによって、2分音符と残りの4分音符とに分割することができる。
このことは等時性スキーマと矛盾しないのだろうか?だが、イベントがその開始点の位置によって理解されることはすでに第2章で述べている。よって、等時性スキーマは、2つ目のイベントが十分な長さを持っていなくても適用することができる。これは、2分音符に続く4分音符を、2分音符の後半部分が失われた2分音符と理解することができるからである。このことは、3拍子の3拍目が、4拍子の3拍目と同じ価値を持っているということをも意味している。バロック時代の理論家が、3拍子の3拍目を強拍としたのはこのような理由によると考えられる。

同様に、2分音符と付点4分音符の比率は4:3であり、2分音符から付点4分音符を分け取ることによって、(3+1)の分割を得ることができる。これは付点リズムに他ならない。これはまた、6/8を、2分音符分で打ち切ったものとみなしても同じである。

これらの分割は拍子に準じた性質を持っている。すなわち、拍子においてそれを構成する拍が、旋律や和声の基本単位となるのと同様に、これらの分割においてもそれぞれが旋律や和声の基本単位となることができる。よってこれらの分割を、拍子に準じるものとして準拍子(quasi-meter)と呼ぶことができる。
(2+1)と(3+1)の準拍子によって追加される書き換え規則は以下の2つである。これらの規則の追加によって、拍節構造を拡張することができる。なお、順序を逆にした(1+2)の分割や(1+3)の分割は、シンコペーションを含むのでここでは扱うことができない。

準拍子としての(3+3+2)の分割
ところで、図4-2.4を見れば明らかなように、準拍子の(2+1)の分割と(3+1)の分割は、それぞれヘミオラを途中で区切った形と全く同じになる。

(3+3+2)の分割はポピュラー音楽で極めて頻繁に見られるものであるが、次の図4-2.5から明らかなように、ヘミオラを少し延長することによって、(3+3+2)の分割も説明することができる。このように理解すると、(3+3+2)の分割は、(2+1)や(3+1)と同列の準拍子として理解することができる。もちろん、(3+3+2)の分割においては、これを構成する3つの部分が拍子における拍と同様の働きをする。図4-2.6には、書き換え規則としての(3+3+2)の分割を示した。


ただし、(3+3+2)の最後の2の理解の仕方には複数の可能性がありうる。単純にヘミオラを延長したものと考える場合には、最後の2は3が途中で打ち切られたものである。他方、すでに述べた(3+1)の準拍子の3の部分に、さらに2分割を適用したものという解釈もありうる。その場合には、音符としては同一の(3+3+2)であるが、3の連続を打ち切った場合とは構造が違っていることになる。これは、同じ単語の連続からなるのに、2通りの文法的解釈が可能な文によく似た現象である。しかし音楽ではそのように複数の解釈が可能な場合というのは全く珍しいことではない。
(3+3+2)の分割は、音符が細分されていると判定が困難になる。例えば次の譜例4-2.1のスコット・ジョプリン(Scott Joplin)の『エンターテイナー』では、(3+3+2)の準拍子の拍が細分化されている。そのような場合には、楽譜に現れる音符の長さの比だけでは、この形を識別できなくなる。図4-2.7に典型的な形だけを抜き出した。


(3+3+2)の分割はしばしばシンコペーションと混同される。シンコペーションは第6章で扱われるのでここで深入りすることはしないが、シンコペーションは第4章までの分割方法では到達できない形であるとだけ述べておこう。ある全体からある拍節単位を、その開始の位置から等時的に順に引き去って行く手続きでは、シンコペーションである(1+2)や(1+2+1)の分割は得られない。
(第1部終わり。第2部は、音楽における「フレージング」の基礎となるフレーズの区分が主題である。この問題に、第1部で確立した拍節の理論を拡張することで対処する。)
カテゴリー:音楽理論
