
それでもボクはやってない:差分プライバシーとは
こんにちは!
コイン投げをすると,コインがどこかに行っちゃう主婦ねこです.
今日はPETsの中でも注目度が高く応用範囲も広い差分プライバシー(Differential Privacy)の紹介をします.このくらいの内容は日本語でもたくさん良い解説(※1)が出ていますが…愛情表現です.
Randomized response
差分プライバシーの話に入る前に,プライバシーを守りながら統計調査をする古典的な手法であるRandomized responseという手法を紹介します.この話から入ると差分プライバシーの概念が理解しやすいと思います.
例えばの話です.たくさんの人を集めて,「あなたは過去に犯罪を犯したことがありますか?」という質問をして,集まっている人たちが,だいたいどれくらい過去に犯罪を犯したことがあるのかを調べたい…とします.この時,普通に質問をすると, 誰が犯罪を犯したことがあるのかわかってしまって,プライバシーを侵害してしまいます.…というより,だれも正直に手を挙げてくれなそうですよね.そこで以下のような工夫をします.これがRandomized responseという手法です.
ひとりひとりにコインを渡してコイン投げをしてもらう.コイン投げはこっそりやって,出た目は秘密です.
コインが表だったら,質問には正直に答えてもらう.もし裏だったら,もう一度コインを投げて,2回目も裏だったら「はい」を,2回目は表だったら「いいえ」を答えてもらう.
このように答えてもらえば,たとえ質問に「はい」と答えた人がいたとしても,本当に犯罪を犯したことがあるのか、それともたまたまコインが2回とも裏だったのか,他人には判断がつきません.
さて,このように質問に答えてもらい,質問に「はい」と答えた人の割合を$${a}$$とします. コインの表裏がそれぞれ$${\frac{1}{2}}$$の確率で出るとき,もともと質問に「はい」だった人,つまり過去に犯罪を犯したことある人の割合を$${p}$$とすると,$${a=\frac{1}{4}+\frac{p}{2}}$$が成り立つことが期待できます.ここから,知りたかった「過去に犯罪を犯したことある人のだいたいの割合」は,Randomized responseの回答を用いて$${p=2(a-\frac{1}{4})}$$と計算できます.めでたし,めでたし.
この話で大切なことは,コイン投げのようなランダム性を入れることで,たとえ都合の悪い情報が開示された場合でも「いやいや,たまたまそういう結果になったんだよ~」という言い逃れをする余地が生まれるというところです.
今回の例はコインの裏表は確率$${\frac{1}{2}}$$で決まりましたが,これがすごーく表が出やすいコインだったらどうなるでしょうか?コインの裏表の出る確率と,質問に答える人のプライバシーの守られ具合にはどんな関係があるのでしょか?
差分プライバシーとは
というような疑問に答えることができるのが差分プライバシー(Differential Privacy)という"指標"です.2006年にCynthia Dworkら(※2)によって考案されました.差分プライバシーという言葉そのものは技術の名前ではないのですが,このあたり言葉の使い方は難しいところです.
Randomized responseで説明したようなランダム性を入れることを,摂動(Perturbation)を加えるとも表現しますが,この摂動を加えるということは古くから統計情報を開示する際に行われてきました.例えば,ある都市に住む人の年収の平均や最大値をそのまま公開するのではなくて,少し摂動を加える,つまりランダムな値(乱数)をちょっと加えた値を公開し,正確な値を出さないようにするなどです.差分プライバシーの基礎的な解説(※3)は,この統計情報への摂動と差分プライバシーの関係からスタートすることが多いので,本ブログでも同様に,統計情報の例から説明して,のちほどRandomized responseの話に戻ることにしましょう.
さて,統計結果にどのような乱数を加えると,どの程度のプライバシが守られるのでしょうか.これを評価する指標としてDowrkらは差分プライバシー(Differential Privacy)を次のように定義しました.

説明します!まず$${D_1}$$と$${D_2}$$というのは,平均や最大値などの統計情報のもとになるデータベースを意味します.この二つのデータベースはたった1レコードだけ異なります.この1レコードがデータベースに含まれているかいないかというプライバシ情報を摂動によってどの程度秘密にできているかを上の式では表しています. $${K}$$はデータベースの平均や最大値を計算し,そこにさらに摂動を加えた値を出力する関数です.そして$${S}$$というのがその出力空間です.下のように書き直した方がわかりやすいかもしれません.
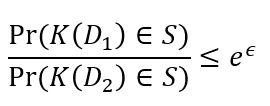
この式は出力空間$${S}$$からある出力$${K(D)}$$得られたときに,その出力のもとになったデータベースが$${D_1}$$である確率と$${D_2}$$である確率の比を評価しています.Dowrkらの論文に$${all \ S\in Range(K)}$$とあることから,すべての出力に対する比の最大値を評価してることがわかります.この比が1に近いほど,ある1つのレコードがデータベースに含まれているかいないかというプライバシ情報を上手く隠せているといえますので,この$${\epsilon}$$の値でプライバシ保護の強さが表せるのです.$${\epsilon=0}$$のときが一番強くプライバシーを保護できている状態ですが,$${\epsilon=0}$$というのはデータベースに関するどんな情報も出力$${S}$$から得られないことを意味していて,これはこれで意味がないことに注意が必要です.
この指標を使って,どういう統計処理結果に対して,どういう摂動をかけると,どれくらいのプライバシーが守られているのかを$${\epsilon}$$で評価することができるようになります.具体的な例を次に書きます.
差分プライバシーによる摂動の評価の具体例
差分プライバシーを用いて摂動の効果を評価するためには,まずクエリ(query)の敏感度(sensitivity)を算出する必要があります.クエリというのは先ほどの例で挙げた平均や最大値などの統計処理を指します.

敏感度とは2つの$${n}$$レコードからなるデータベース$${D^n}$$のクエリ(上記の図ではfunctionに相当)$${f}$$によって生じる差の最大値です.この2つのデータベースとして先ほどお話しした1レコードだけ異なる2つのデータベースの差の最大値をまずは評価します.
例えばレコードの値が0か1のどちらかを取るとします.例えばクエリが「データベースのレコードの最大値」だとします.すると1レコードだけ異なる2つのデータベース$${D_1^{n}, D_2^{n}}$$で差が最大になるのは,$${D_1^{n}}$$がすべてのレコードが0の時で,$${D_2^{n}}$$が1レコードだけ1でほかのレコードが0の時.なのでこの時の敏感度は1です.クエリが「データベースのレコードの平均値」の場合は,1レコードだけ異なるならば,この時の差は$${\frac{1}{n}}$$です.平均より最大値の方が敏感度が高いことがわかります.
最大値や平均値に対してスケールパラメータが$${\frac{S(f)}{\epsilon}}$$のラプラスノイズを加えると,その出力が$${\epsilon}$$-差分プライバシを満たすことが知られています.
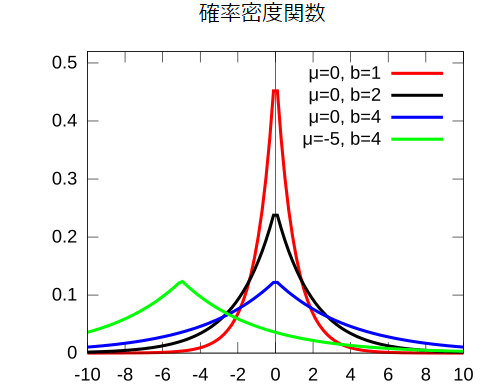
スケールパラメータとはラプラス分布の広がり具合を表す値で,上の図でいうと$${b}$$の値です.$${b}$$の値が大きいほど(敏感度が高いほど,また,$${\epsilon}$$の値が小さい,つまり,高いプライバシを担保しようとするほど),強いノイズが必要になることがわかります.
このように,どんな乱数を加えると,どのくらいのプライバシが担保できるのかの関係を明らかにすることができるのが,差分プライバシの価値なのです.
Randomized responseを差分プライバシーで評価すると
Grobal Differential PrivacyとLocal Differential Privacy
Randomized responseの場合は入力は,統計情報の出力という話ではないので,ちょっと違う定義(※4)を使って評価します.

クエリの概念がないので,直接二つの入力$${v,v'}$$をアルゴリズム$${\pi}$$に入れた時の出力の差を評価します.
統計量の出力を考える場合をGlobal Differential Privacy,入力値に直接摂動をかける出力する場合をLocal Differential Privacyと呼び,区別することが多いです.

別の記事で,上の図を出してPETsの分類をしましたが,図のようにLocal Differential Privacyは個人からデータを収集するときの摂動の評価に利用されることが多く,Grobal Differential Privacyはたくさんのデータを持っている法人がデータの統計量を公開するときの摂動の評価に利用されることが多いです.が,あくまでも統計量を摂動の対象とするか,データそのものを摂動の対象とするかでGlobalかLocalかが決まることに注意してください.
Randomized responseをLocal Differential Privacyで評価すると
では,Local Differential Privacyを用いてRandomized responseの評価をしてみましょう.
まず入力は「はい」か「いいえ」の2つなので$${v}$$が「はい」、$${v'}$$が「いいえ」だとします.実際にはすべての取りうる入力ペアについて考えます.アルゴリズム$${\pi}$$はRandomized responseのやり方そのものを意味します.Randomized responseの結果も「はい」か「いいえ」ですので$${y}$$も「はい」と「いいえ」の場合を考えればよいです.
元々の答え$${v}$$が「はい」で,Randomized responseの結果$${y}$$が「はい」になる確率$${Pr(\pi(v)=y)}$$は,コイン投げで表が出て正直に答える場合($${\frac{1}{2}}$$)と,コイン投げで裏が出て,その後,また裏が出た場合($${\frac{1}{4}}$$)なので$${Pr(\pi(v)=y)=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}}$$です.
一方,元々の答えが$${v}$$が「いいえ」で,Randomized responseの結果$${y}$$が「はい」になる確率$${Pr(\pi(v’)=y)}$$は,コイン投げで裏が出て,その後,今度は表が出た場合($${\frac{1}{4}}$$)なので$${{Pr(\pi(v)=y)}=\frac{1}{4}}$$です.よってその比は$${3}$$になります.Randomized responseの結果$${y}$$が「いいえ」になる場合も似たように考えて最大値を取ります.最大値はやっぱり$${3}$$になります.
よってRandomized responseは$${\epsilon=\ln(3)}$$-差分プライバシーを満たすといえます.
ここで最初のコイン投げで裏が出る確率を$${f}$$と置くと(2回目は裏表が$${\frac{1}{2}}$$で出るとします),$${\epsilon=\ln(\frac{1-\frac{1}{2}f}{\frac{1}{2}f})}$$となります.$${f=1}$$つまりコインが絶対に裏しか出ない時は$${\epsilon=\ln(1)=0}$$になるのでプライバシの強度としては最強です.コインに任せて「はい」と「いいえ」を答えているだけなので,そりゃそうです.$${f=0}$$の時は分母が0になってしまうので不定です.実際この場合は,100%質問に正直に答えることになるのでプライバシもなにもないですね.$${f}$$の値が大きいほど(正直に答える確率が下がるほど)高いプライバシが担保できるようになっているのがわかるかと思います.
んでεっていくつがいいの?
「$${\epsilon}$$が小さいほど良いことはわかった.で,具体的には$${\epsilon}$$がどれくらいだったらいいの?」という疑問はFAQだと思います.専門家の間では$${\epsilon=0.1}$$くらいが良いという事を言う方が多い印象ですが,論文によっては一桁ならOKと書いてある場合もあります.
$${\epsilon}$$が大きい方が,摂動よるデータの劣化は少なくて済むので,$${\epsilon}$$をすごく大きく設定した上で「プライバシ保護とデータ活用が両立できる技術を作りました!」と主張する論文もあります.こういう技術はチートDP(Cheating DP)と揶揄されていますが,たとえどんなに$${\epsilon}$$の値がどんなに大きくても摂動されている限りは
「それでもボクはやってない」
と言えますし,その可能性はゼロではありません.
(6000文字書いて,ようやくタイトル回収!!!)
おまけ:そういうわけで私は$${\epsilon}$$の値がちょっとくらい大きくてもいいんじゃないの派です.証拠さえ押さえられなければOKOK.
おまけ2: 社内の従業員満足度調査のアンケート結果にも摂動かけて欲しいですよね.「5名以下の回答は開示しません」とか注意書きがしてあるけど,5人以上のチームメンバ全員が「1:上司はクソ」を選択したらどうしてくれんだよ…と思って,いつも忖度しちゃうんですよねー.
参考情報
(※1)こちらからダウンロードできる解説記事がおススメです!
(※2)Dwork, Cynthia. "Differential privacy." International colloquium on automata, languages, and programming. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006.
(※3)私はまずは以下の書籍で勉強しました.ゼロ知識証明を除くPETsが網羅的に紹介されていますが、著者の佐久間先生のご専門は差分プライバシーなので,差分プライバシーの説明が一番手厚いです.Randomized Responseの話から始める解説もこちらの書籍のマネっこです(汗).
(※4) Bebensee, Björn. "Local differential privacy: a tutorial." arXiv preprint arXiv:1907.11908 (2019).
Local differential privacyの初出は諸説あるようなので,チュートリアル論文から定義を抜粋しました.
(※) 「それでもボクはやってない」.じつは未視聴です…すみません.
※アイキャッチ画像はDALL-E3にて作成しました.Randomized responseをやっているネコたち…風です.
