
電卓で学ぶ『アルマゲスト』 ~太陽の軌道篇~
序.
本稿では,紀元後二世紀,エジプトのアレクサンドリアの天文学者プトレマイオスが書いた『アルマゲスト』第3巻における太陽の軌道計算を題材にし,理論の説明だけではなく,電卓を用いて計算することで, 古代天文学のテクニカルな議論を知っていただこうと思います.はじめに計算の前提となる天文学の知識を確認しておきましょう.
1.星と暦
我々は普段,365日と4年に一度の閏日の挿入により1年を把握していますが,古代ギリシャ人はどのような暦を使っていたのでしょうか?古代ギリシャでは月の満ち欠け(朔望)に基づく「太陰暦」が使用されていましたが,太陰暦には四季と同期しないという難点があります.
古代ギリシャだけではなく,殆どの地域で暦は朔望周期に基づいていました.約29.53(日)×12(ヶ月)=354.36(日)となり,朔望周期は1年の長さ約365.25(日)と一致しません
そこで,農業では四季を知る必要があるため,月の周期とは無関係の「農事暦」というものが考案されていました.ヘシオドス『仕事と日』(前700年頃)に次の様に書かれてあります.
アトラースの姫御子,プレーイアデスが昇る頃に
刈り入れ,その沈む頃に耕耘を始めよ.
ヘシオドスの時代には5月中旬に観測されるプレイアデス(和名:昴)が,夜明け直前に昇る現象(ヘリアカルライジング)が,刈り入れの合図として用いられていたことが分かります.このように農事暦は恒星(や星座)の出没を目印にして運用されていました(なおエジプトでは,シリウスのヘリアカルライジングを1年の起点としました).

太陰暦と1年(太陽年)の同期の問題は閏月の挿入の問題として残されてはいましたが,農事暦により実用上の問題はほぼなかったといえます.
次に哲学者が宇宙を考えた方法を見てみましょう.古代人の宇宙観の変遷についてはこちらのnoteを参考にしてください.
2.現象を救う
古代人は恒星が貼り付いた球が,静止する地球を中心にして一日で一回転すると想定していましたが,季節によって太陽が昇ってくる星座が異なるため,太陽と恒星は同じ速度で回転していないことがわかります.

哲学者プラトンは『ティマイオス』にて,時間とは天体の運行のことであるという提案をしたことを知っておく必要があります.
夜と昼という,単一で,最も知的な円運動の周期が生じたのでした.また,月が自分の円を一巡して太陽に追いつく時には暦月が,また,太陽が自分の円を回り了える時に暦年が生じます.
そしてプラトンは,このような天体の複雑な動きを幾何学で説明するように号令を出したと伝承されています.まず,プラトン自身による『ティマイオス』での説明を見てみましょう.
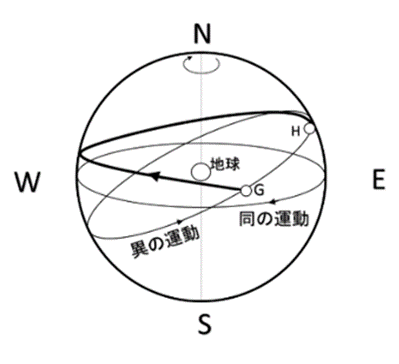
天体G(太陽や月を含む惑星)の動きは「同の運動(水平方向への東から西への運動)」と「異の運動(上下方向への西から東への運動)」の合成運動として表現されています.恒星(天球)と一緒に1日で1回転する「同の運動」をしながら,惑星固有の「異の運動」をすることで,「螺旋状」の運動をすると想定しました.

プラトンの号令を受けたのかどうか,はっきりしたことは不明ですが,古代ギリシャの天文学者は,幾何学的なモデルによって天体の動きを説明することになりました.
また,観測技術の進歩より「四季の不均等」が前5世紀末には知られるようになっていましたが,前4世紀の哲学者は,この四季の不均等を幾何学的に表現することに成功せず(※カリッポスというアリストテレスと同時代の天文学者が成功しましたが,彼のモデルは継承されませんでした),前3世紀以降に考案された離心円モデルにより,四季の不均等を説明するモデルを提示することに成功したのです.本稿で説明する『アルマゲスト』のモデルは,この離心円モデルの説明です.
その前に四季の不均等の現代的な説明を確認しておきましょう.
3.太陽中心モデル(地動説)
ケプラーによる惑星の楕円軌道の発見により,私たちは,地球が太陽を焦点の一つをする楕円軌道上を周回していることを知っています.

しかし,楕円とはいっても,その長径と短径の比は100000/99986であり,地球の軌道は非常に円に近い楕円なのです.一方,プトレマイオスは地球が宇宙の中心に静止し,天空が回転すると考えていました.これを一般的には「天動説」と呼びますが,歴史的には「地球中心説」と呼ぶ方が正確です.
実は,天体の軌道が完全な円軌道であれば,太陽と地球のどちらが中心かは,数学的には重要ではありません.ケプラーの太陽中心説の重要な点は,地球が動いているという事よりも,楕円軌道を含む「ケプラーの法則」の提唱にあるのです.
その「ケプラーの法則」では「面積速度一定の法則」が証明されています.これは近日点(太陽に最も近い点)では惑星(地球を含む)は速くなり,遠日点(太陽から最も遠い点)では惑星は遅くなることを意味します.

夏至は遠日点の近くで起こるため,地球の公転速度は遅くなり,冬至はその逆で速くなります.これが四季の不均等の現代の説明です.
地球中心説において,太陽の速度の変化を説明可能なモデルが「離心円」です.『アルマゲスト』では,太陽の移動速度は変化せず,移動する距離を長くすることで,見かけの速度を変化させて説明します.

では,具体的にどうやって「見かけの速度」を変化させるのかというと,太陽の回転の中心を地球ではなく,少し離れた点に設定します.これを「離心円モデル」と呼びます.

『アルマゲスト』では離心円の他にも「周転円」というモデルにより太陽の軌道を説明しますが,本編では扱わず,付録として末尾で説明します.
図をみると,Q͡K > L͡M となっていることが分かります.太陽は一定速度で周回していると想定するため,QからKへの移動時間はLからMへの移動時間より長くなり,これが四季の不均等を生み出します.この太陽の中心の位置を計算で求めるのが本稿の主題です.
実際に計算に入る前に,「弦の表」について確認しておきましょう.
4.弦の表
実際の計算では現代の三角関数表に相当する「弦の表」を用います.
1/2°から180°まで,1/2°毎の弦の長さを表にしたものです.
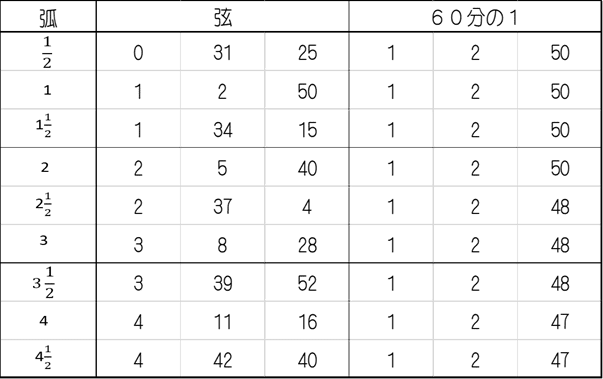
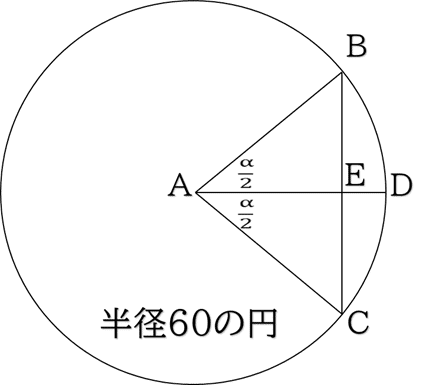
例えば,弧=3° つまり B͡C=3°のとき,弦の表から「 3 8 28 」を拾ってきます.これは次の数を意味します.
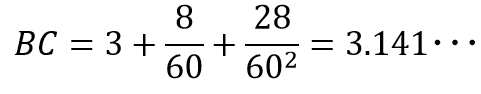
三角関数を用いて計算すると
BC=60・2・sin1.5°=3.14123・・・となります.
なお,角BACの弦BCを求めるというのは,sin ∡BAEを2倍にしたものを求めることと同値です.
弦の表の右欄「60分の1」は,1/2°毎の弦の長さを30で割ったものです(つまり1°を60で割ったもの).これは1/2°より小さい弦の値を求めるときに使用します(後述).
『アルマゲスト』では,太陽の軌道計算において,4°+20°/60(4.33°)の弦の値が必要になります.この値をどのように表から引いてくるのでしょうか.
まず4°の値は
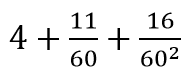
4° と 4°+1°/2 との弦の長さの差を60で割った値は

この数値を20倍したものを,4°の弦の値に加えることで, 4+20°/60の値とします.これを計算すると,4.536574074となり,三角関数で計算した4.536774588 と,小数第3桁まで一致します.この弦の表の作成についてはこちらのnoteをご覧ください.
※ 一般に,弦(B͡D)+弦(C͡D)=弦(B͡C) とはなりませんが,ここでは十分に角度が小さいため近似的に上式が成立します.
本稿の計算は電卓を用いて行うため,分数を使用しません.また,小数第五桁までを有効数字とし,それ以下を切り捨てます.よって『アルマゲスト』における数値とは完全には一致しませんが,証明の手順は原典を尊重してあります.
5.実際の計算
太陽が周回する離心円の大きさを決定するには,1年の長さを知る必要があります.プトレマイオスはヒッパルコス(前2世紀)の計測した値を引用し,1年の長さとして次の値を利用します.

地球を点Eとし,春分点をA,夏至点をBとします.太陽は円QKL上を周回します.点Qに太陽があるときが春分です.ヒッパルコスは春分から夏至までを 94.5日,夏至から秋分までを 92.5日と観測しました.この観測からQ͡KとK͡Lの大きさを求めます.

U͡Q=4.31379° からUQの長さを「弦の表」から求めます.「弦の表」も小数表示に変更しておきましょう.

1/60°=0.01666 ですので,「60分の1」は 0.01666° 毎の値です.
0.31379/0.01666 = 18.83493
よって,0.01744を18.83493倍したものを 4.18778 に加えます.

ここで,UQ = 2QT = 2EC より,EC = 2.25813 となります.
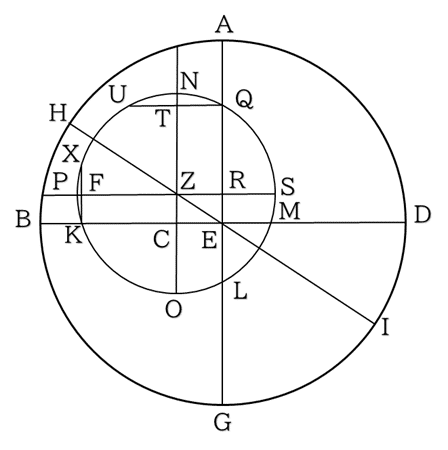
ここで,Q͡K=93.14253° ,また Q͡N=2.15689° だから

2P͡K = 2K͡X = 1.97128° より,KXの長さを「弦の表」より求めます.
これは U͡Q=4.31379° を求めた方法と同じやり方.結果は KY=2.06445° となりますが,電卓で再現してみてください.
KX=2.06445 より,KF=ZC=1.03222 また,EC = 2.25813である.
ここで△EZCに三平方の定理を用いて,EZを決定します.
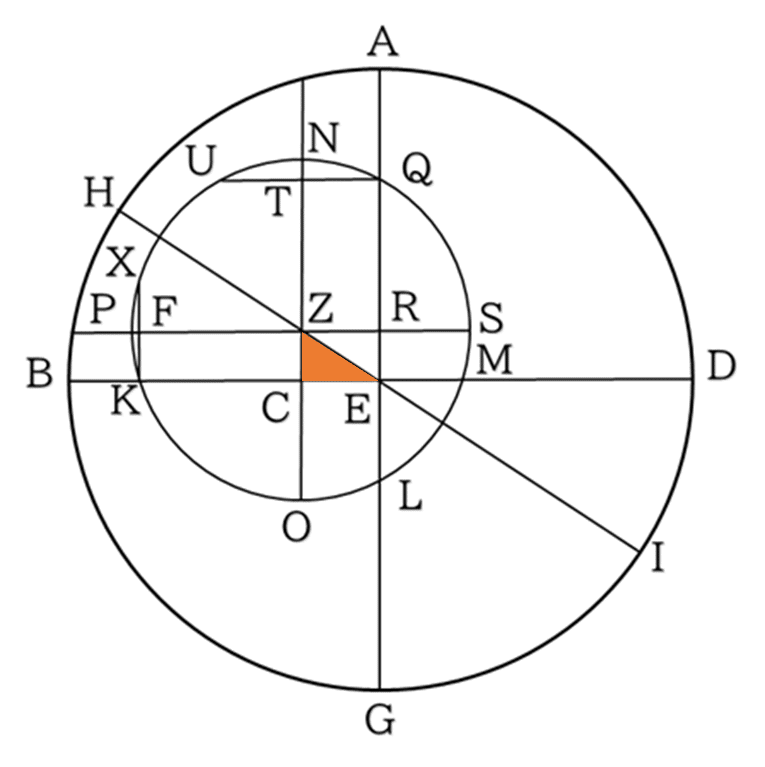
「ECとZC上の正方形を一緒にしたものは,EZ上の正方形を作る」というような表現をします.

よって,太陽の離心円の半径は,地球と離心の中心の距離の約24倍となります.
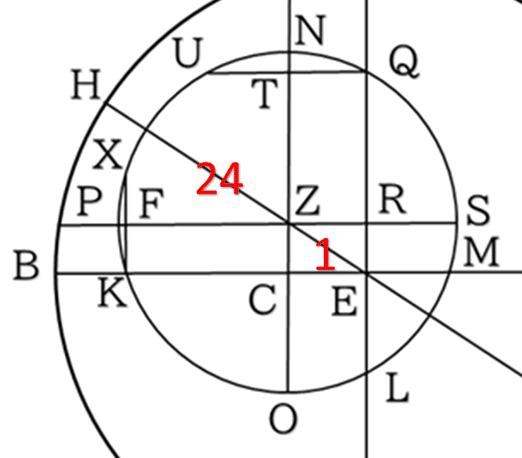
さらに,∡ZECを求めることで,太陽の遠地点Hの方向を決定します.
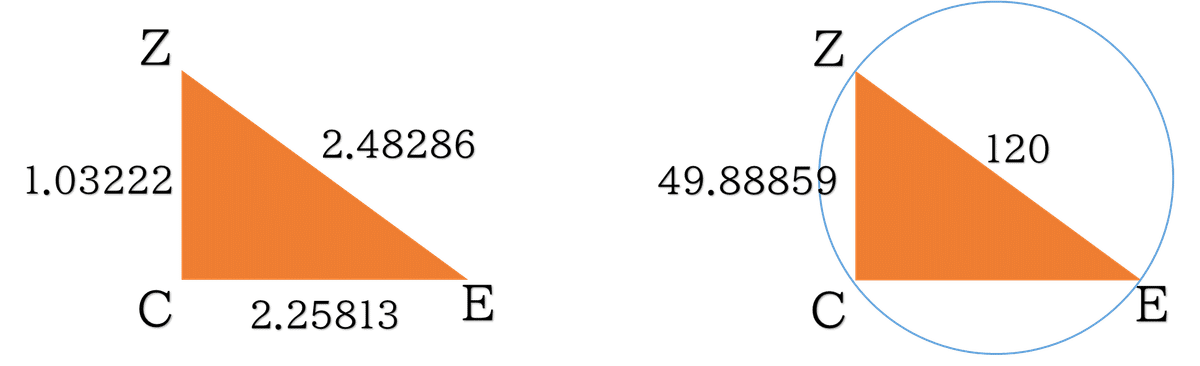
ここで「弦の表」を逆引きすることで,弦ZCの値からZ͡Cを求めます.

『アルマゲスト』では,ZC=49.8859 に最も近い 49° をもってZ͡Cの値とします.

よって,太陽の遠日点HはB͡H=24.5°となる方向にあることになります.以上で,地球を点Eとしたとき,太陽の離心円の中心Zまでの距離と方向を決定できました.『アルマゲスト』では,同様の計算により「秋分~冬至~春分」の長さを決定します.ここまで読んでくださった方は,計算に挑戦してみてください.

最後に
実際の計算により古代の天文学の内容をご理解いただけましたでしょうか?太陽の軌道計算に必要な観測データは「1年の長さ,春分から夏至,夏至から秋分までの長さ」の3つだけという非常にシンプルなものでした.
また,『アルマゲスト』では離心円の中心を決定することで,太陽の位置を予測可能になりましたが,太陽と地球の距離は不明です.
太陽が遠地点にあるとき
(太陽~離心円の中心):(離心円の中心~地球)= 24 : 1
という距離の比例関係が分かるだけです.太陽や月のようなある程度の見かけの大きさをもつ天体までの距離は,第5巻で計算されますが,火星などの惑星までの距離は『アルマゲスト』の理論では全く扱うことができない問題として残されました.この難題は,プトレマイオスに続く天文学者たちに研究テーマの1つとして継承されています.
一気に時代を下りますが,コペルニクスが提唱した太陽中心説は,この惑星の距離の問題を,観測値から議論することができるという点で「革新的」だったのです.
付録
『アルマゲスト』では,太陽の軌道に離心円の他に周転円というモデルを提案します.惑星(ここでは太陽のこと)の軌道は,導円上を回る小円(周転円)として表わされます.
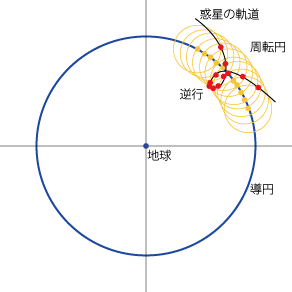
https://eco.mtk.nao.ac.jp/koyomi/wiki/A5A2A5EBA5DEA5B2A5B9A5C8.html
この周転円モデルと離心円モデルが,幾何学的には同値であることを証明するのですが,本稿では,三角関数を用いて簡単に確認しておきましょう.
地球を点E,半径rの離心円の中心を点Z,太陽を点Kとします.
すると,太陽の方向は tanα で表すことができます.

次に周転円です.地球を点Zとし,導円の半径をr,太陽は周転円上の点Vです.この太陽の方向もtanαで表わすことができます.

このように,離心円と周転円ともに,tanα の値は等しくなります.よって離心円と周転円が幾何学的に同値であることが分かります.
参考文献
・プトレマイオス(藪内清 訳)『アルマゲスト』 恒星社厚生閣(1993年)
現在(2021年)のところ唯一の邦訳(フランス語訳の重訳)です.
・G. J. Toomer ,Ptolemy's Almagest ,Prinston(1998)
最も参照されることの多い定番の翻訳.藪内訳とは底本が異なるため章立が異なります.
・『西洋哲学史 1 「ある」の衝撃からはじまる』 講談社選書メチエ(2011年)から第3章
プラトンが天文学の展開に与えた影響について,否定的に検討したもの.
・渡辺雅雄編『科学の世界』共立出版(1982年)から第1章
古代から近世までの計算天文学の展開を概観できます.
・クリストファー・ウォーカー (山本啓二 /川和田晶子 訳)『望遠鏡以前の天文学』恒星社厚生閣(2008年)から第3章
古代ギリシャ天文学の通史を学べます.
