
電卓で作るプトレマイオスの「弦の表」
序.
『アルマゲスト』第1巻に収録されている「弦の表」の作成法について解説します.『アルマゲスト』における実際の「弦の表」の利用についてはこちらのnoteをご覧ください.
https://note.com/greekmathematics/n/nbe51ec97f4b5
1.「弦の表」とは
「弦の表」とは,半径60の円において,1/2°から180°までの弧に対する弦の長さを1/2°毎に計算したものです.

つまり,B͡Cと弦BCの関係を表にしたものです.B͡C= α とすれば

と表わすことができ,1/4°毎の正弦の表に相当します.
『アルマゲスト』第3巻の太陽の軌道計算では 4°20′ (4度20分=4°+20°/60を意味します)の弦の値が必要になります.本稿ではこの値を得るための計算の手順をご説明いたします.
2.計算の手順
プトレマイオスがこれらの値を決定するのに用いるのは,「トレミーの定理」と「半角の定理」,「弦と弧の不等式」です.これらを組み合わせることで,目当ての値を得ます.4°20′を得るための道筋を図にしました.弦の表は0.5°毎の値ですので,私たちはまず4.5°と4°の値を得ることになります.

それでは72°から始めます.
3.正5角形と正10角形
36°の弦は,正10角形の1辺の長さにあたります.これは三角形の相似を利用して決定できます.

本稿では,小数第5桁を有効数字とし,6桁以下を切り捨てます.
よって 弦(36°)=37.08203
次に72°の弦ですが,これは『原論』13巻命題10で扱われます.
AFは正3角形,ABは正5角形,そしてAKは正10角形の1辺となります.

△BFA∽△BNF より BF:AB=BN:BF
△ABK∽△AKN より AK:AB=AN:AK
よって BF²=AB・BN, AK²=AB・AN
BF²+AK²=AB(BN+AN)
ゆえに BF²+AK²=AB²
BF=60,AK=37.08203 より
弦(72°)=70.53422

4.トレミーの定理
円に内接する四角形についての定理です.トレミー(Ptolemy)とは『アルマゲスト』の著者プトレマイオスの英語名です.
AC・BD=AB・CD+BC・AD をここでは三角形の相似を利用して証明します.
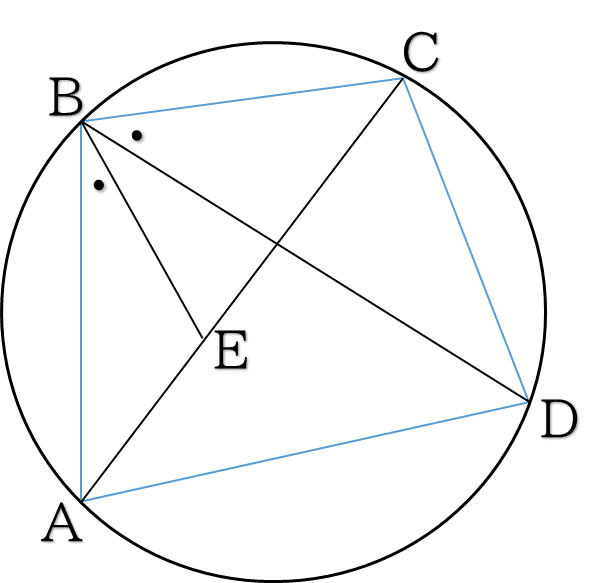
△ABD∽△EBC,△ABE∽△DBCより BD・CE=BC・AD ,BD・AE=BA・DC
よって BD(CE+AE)=AB・CD+BC・AD
∴ AC・BD=AB・CD+BC・AD
この定理を利用して弦(12°)を求めます.

AD²=120²,AB²=60² より BD=103.92304
AD²=120²,AC²=70.53422² より CD=97.08204
ここでトレミーの定理より
70.53422・103.92304=60・97.08204+弦(12°)・120
よって 弦(12°)= 12.54340

次に18°と6°を計算していきます.
5.半角の定理
半角の計算は,トレミーの定理でも可能ですが,ここでは「半角の定理(公式)」を利用して計算を続けましょう.

弦(12°)=BC から,弦(6°)を計算することができます.
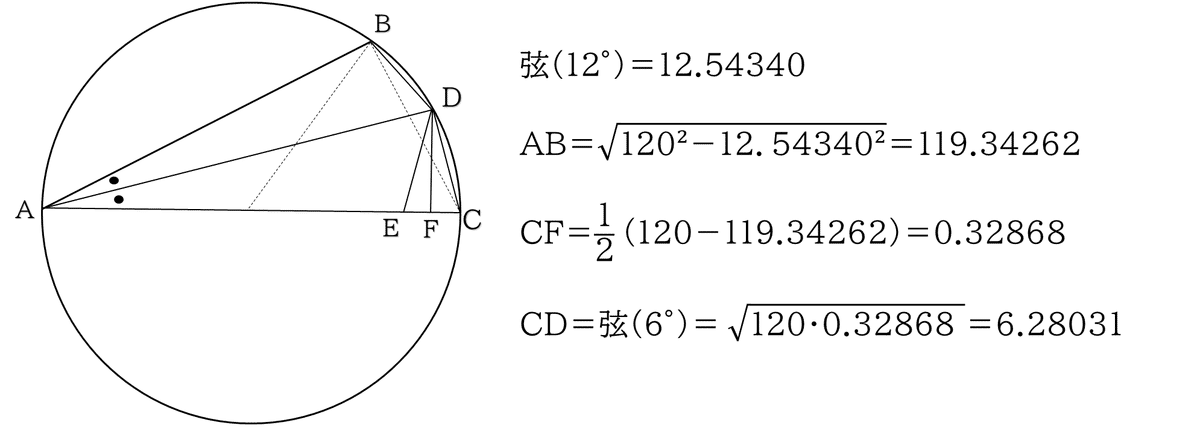
弦(6°)=6.28031 を計算できました.この半角の定理を用いて,
弦(18°),弦(9°),弦(4.5°),弦(3°),弦(1.5°),弦(0.75°)を計算していきます.

『アルマゲスト』の計算(を小数に直したもの)と関数電卓による計算を表にしました.半角の定理と電卓を用いて,古代人の計算の執念を感じてみてください.

6.弦と弧の不等式
ここまでの手順では,1°の値を求めることができません.これをプトレマイオスは不等式による評価で巧妙に計算します.証明する関係は,
B͡C : E͡F < BC : EF
つまり,弧の大きさに比例して,弦は大きくはならないということです.この関係は,前4世紀には知られていたようですが,証明は『アルマゲスト』が初出です.

それではプトレマイオスの証明を見てみましょう.

∡ABD=∡CBDのとき,CD=AD となります(これは『原論』3巻命題26,29で証明されています.)
また,CE>EA(これは『原論』4巻命題3で証明されています)
ここで DF⊥AC とすると,DA>DE>DF
また,半径をDGとし点Dを中心とする円を描くと
△DEF:△DEA < 扇形DEH:扇形DEG
よって FE:EA<∡FDE:∡EDA
よって FA:EA<∡FDA:∡EDA
CA:AE<∡CDA:∡ADE
ここで CE:EA=CB:BA
また ∡CDE:∡EDA= C͡B:B͡A
∴ CB:BA< C͡B:B͡A
この不等式を次のように用います.
3:2=1.5°: 1° >弦(1.5°):弦(1°)
4:3= 1° :0.75°>弦(1°) :弦(0.75°)
ゆえに次の不等式が成立します.
(2/3)・弦(1.5°)<弦(1°)<(4/3)・弦(0.75°)
(2/3)・弦(1.5°) = 1.04716
(4/3)・弦(0.75°)= 1.04718
1.04716< 弦(1°)<1.04718
関数電卓による計算では 1.04718 となりますので,本稿ではこの値を採用します.一方,プトレマイオスは 1;2’ 50”=1.04722 を弦(1°)として採用しました.

残るは,2°と4°の計算です.
7.倍角の定理
半角の定理を逆に辿ると倍角の弦を求めることができます.

弦(2°)=2.09333
同様に,弦(2°)から弦(4°)を計算できます.
弦(4°)=4.18604
お疲れ様でした.ついに4°と4.5°の弦の値を求めることができました.プトレマイオスはこのような手順を繰り返すことで「弦の表」を完成させたのです.ところで,『アルマゲスト』では,4°20′(=4.33333°) のような0.5°よりも小さい弦の値が必要になります.これはどのように計算したのでしょうか.
8.「60分の1」
既にみたように,弦の大きさは弧の大きさに比例しません.つまり
sinθ+sinθ=sin2θ は成立しないのですが,弧の大きさが十分に小さいとき,近似的にこの関係は成り立ちます.たとえば,
sin0.1°=0.10471
sin0.2°=0.20943
よって,2sin0.1°=0.20942≒0.20943=sin0.2° となります.
プトレマイオスはこのことを利用し,「弦の表」の各数値の差を30で割ることで,1/60°(0.01666)毎の弦の値を得ます.
具体的にみてみましょう.
弦(4.5°)ー弦(4°)=4.71118ー4.18793=0.52325
0.52325/30 = 0.01744
よって,4°~4.5°の間に,弦は 1/60° 毎に 0.01744 ずつ大きくなります.関数電卓による計算と比較しても十分な精度を達成していることが分かります.

これで, 4°20′(=4.33333°)の弦の値を知ることができました.
弦(4°20’)= 4.53673 となります.
9.おわりに
プトレマイオスは次のようにいいます.
さらに,私どもは常により近い〔値〕を目指して,乗法や除法を,その量[誤差]を無視しても,感覚的に正確な量と大きな差が生じないくらいに進めます.
この研究方針こそが,『アルマゲスト』における成功の要因の1つといえます.そして『原論』に象徴されるような計算や近似とは無縁のギリシャ数学の違った側面を教えてくれます.
ところで,私たちは,小数を利用することで『アルマゲスト』における近似計算の実際を学んできました.ですが,プトレマイオスが実際に使用したのは60進法の分数だったということは忘れてはいけません.
参考文献
・プトレマイオス(藪内清 訳)『アルマゲスト』 恒星社厚生閣(1993年)
・『教育科学 数学教育』明治図書,2013年 10月号,52-57頁
・T. L. Heath, Aristarchus of Samos, Cambridge (1913)
・山本義隆『小数と対数の発見』日本評論社 (2018年)
