
微分・積分【学習ノート】

積分は単位の掛け算/微分は単位の割り算
積分は単位の掛け算であり面積として求められる
微分は単位の割り算であり傾きとして求められる
積分:すべてを面積としてとらえる
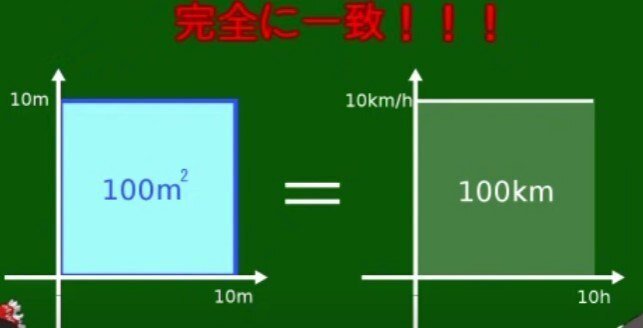
縦10m・横10mの正方形の面積は……10m✕10m=100m^2
時速10kmで10時間走ったときの距離は……10km/h✕10h=100km

底辺10m・高さ10mの三角形の面積は……10m✕10m/2=50m^2
初速0kmで加速度が1km/h^2で10時間経ったたときの移動距離は……10km/h✕10h/2=50km
単位が違えばグラフも違ってくる
積分の場合「単位を掛けたものが求めたいもの」になっているかが重要

微分:すべてを傾きとしてとらえる(変化量)
例:時速……1時間あたり距離がどれだけ変化するか
加速度……1時間あたり速度がどれだけ変化するか
上記左側のグラフは加速度を、右側のグラフは速度を表している
km/h/h……km/h^2(加速度) km/h……km/h(速度)
微分とは何か?直感でわかる微分、なぜ微分をするのか、日常に潜む微分、微分をする意義
積分とは何か?「積分」って「微分の逆」なの?(積分の歴史、意味、なぜ積分が必要か、素朴な疑問を解決します!)
【直感でわかる積分】なぜ積分で面積が求まるのか?視覚的イメージでわかりやすく解説!
積分で面積が求まるのはなぜ?ー定積分をイメージでとらえる
世界は微分で記述され積分で読み解く
関数(function)とは:変換装置/数と数の間の関係
グラフとは:入力と出力の関係を図示したもの
微分とは傾き:限りなく小さな変化を観ること
積分とは面積:限りなく小さい変化を足していくこと
