漁具形状の科学的な設計とは?
今回は、以下の論文を紹介します。
CFD解析を用いたオッターボードの形状最適化手法
高橋勇樹, 藤森康澄, 胡夫祥, 木村暢夫
日本水産学会誌 83(6) 950-960 2017年
この論文は、前回記事の続きともいえる論文です。
前回の記事を読んでいなくても問題ないですが、お時間があるようでしたらこちらの記事もぜひ。
「最適な」オッターボードの設計
前回の論文で、オッターボード設計にCFD解析を活用できることを確認しました。
改めて、下の図がオッタートロールの概要図です。
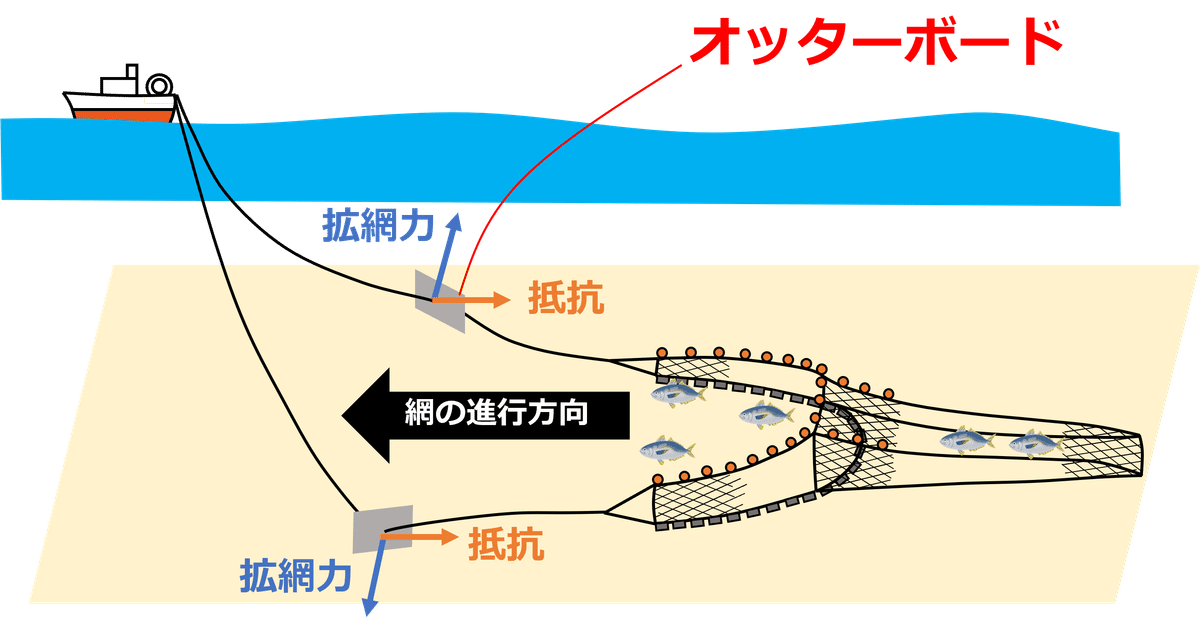
オッターボードは網を広げるために用いられる漁具なので、網を広げるための力(拡網力)を大きくする必要があります。
また、抵抗が大きいと船で引っ張りにくくなり、余計な燃料を消費してしまうため、流れから受ける抵抗はできるだけ小さい方が望ましいです。
よって
「拡網力ができるだけ大きく、かつ抵抗ができるだけ小さい」
オッターボードが望ましいといえます。
厳密に言うと
①拡網力を最大化する
②抵抗を最小化する
という、①と②を同時に満たすようなオッターボード形状を見つけることがここでの設計の目標です。
科学的な設計とは
ここで、科学的な設計についてお話ししたいと思います。
ここでいう設計とは、
「目的変数を最大化する(あるいは最小化する)設計変数の組み合わせを見つけること」
といえます。
例として、できるだけ美味しい白ご飯を炊きたい場合を考えます。
白ご飯の美味しさを最大化する、という事になります。
できるだけ美味しいご飯を炊くために、調理者はお米の量、水の量、火の強さ、火にかける時間、蒸らす時間を変更できるとします。
以上のような状況では、設計は以下のようになります。
設計変数:お米の量、水の量、火の強さ、火にかける時間、蒸らす時間
目的変数:美味しさ
つまり、
美味しさ(目的変数)を最大化するお米の量、水の量、火にかける時間、蒸らす時間(設計変数)の組み合わせを見つけること
が、ご飯の「設計」です。
話をオッターボードに戻します。
改めて、以下が複葉型オッターボードの概要図です。
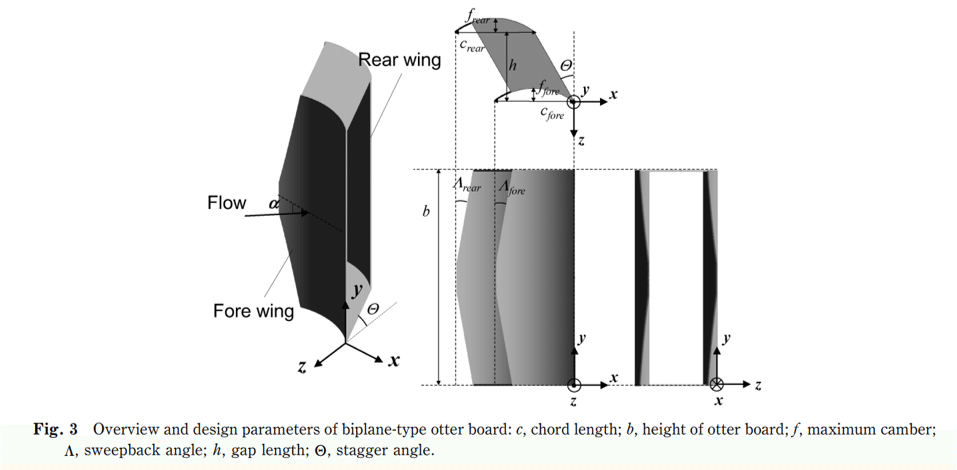
引用元:CFD解析を用いたオッターボードの形状最適化手法. 高橋勇樹, 藤森康澄, 胡夫祥, 木村暢夫日本水産学会誌 83(6) 950-960 2017年
https://doi.org/10.2331/suisan.16-00076
複葉型オッターボードでは、以下の8つの設計変数を持ちます。
①前翼の反り比(f_fore)
②前翼の翼弦長(c_fore)
③前翼の後退角(Λ_fore)
④後翼の反り比(f_rear)
⑤後翼の翼弦長(c_rear)
⑥後翼の後退角(Λ_rear)
⑦前翼と後翼の間隔(h)
⑧前翼と後翼の設置角度(Θ)
つまり、この研究での最適設計は
拡網力を最大化し、抵抗を最小化するような、①~⑧の値の組み合わせを見つけること
と定義することができます。
この設計の難しさ
ただ、この複葉型オッターボードの設計を行おうとした際に、困難さに突き当たりました。
具体的には、①設計変数が多いこと、②目的変数が複数あることがここでの最適設計を難しくしています。
①設計変数が多いこと
複葉型オッターボードは比較的複雑な形状をしており、設計変数は前述の通り8つあります。
例えば、8つの設計変数について、それぞれ4通りの値を設けて、すべての組み合わせで拡網力と抵抗を確かめようとすると、
4通り×4通り×4通り×4通り×4通り×4通り×4通り×4通り=65,536通り
となってしまい、6万通り以上の組み合わせをシミュレーションする必要があります。
いくらCFD解析によって効率的に漁具設計ができるようになったといっても、一つのオッターボードに対して、6万通り以上の組み合わせを試すのは、さすがに現実的ではありません。
②目的変数が複数あること
先ほどのご飯の例では、目的変数は「美味しさ」だけでした。
しかし、オッターボードでは、
①拡網力を最大化する
②抵抗を最小化する
という、二つの目的があります。
このとき、設計は複雑になります。
なぜかというと、こうした目的変数はトレードオフの関係になることが多いためです。
トレードオフとは、「あちらを立てれば、こちらが立たず」というような状況です。
ここでの例で言うと、
拡網力を大きくしようとすると抵抗も大きくなってしまう
逆もしかりで、
抵抗を小さくしようとすると拡網力も小さくなってしまう
という事です。
本研究でのプロセス
そこで本研究では、過去の研究を参考に、色々な工夫によって複葉型オッターボードの設計を試みました。
具体的には、以下のプロセスで上記の問題を解決しました。
(少し込み入った話になりますので、読み飛ばしていただいても問題ありません。)
①統計的な分析により、設計変数を主要なものに絞る
②選択された設計変数を対象に直交表を用いてCFD解析を行い、拡網力と抵抗を計算する
③応答曲面法により、設計変数と目的変数の間の関係性を推定する
④応答曲面を用いて、多目的最適化手法によって、最適な設計変数の組み合わせを見つける
まず①で統計的な手法を使って、拡網力と抵抗力に大きく影響を与える設計変数を調査し、対象の設計変数を8個から4個に削減します。
4つに減らしたとしても、全通り解析するのはまだ難しいです。
そこで、②で直交表という実験表を使って、シミュレーションするオッターボードを64通りに絞り込んで、CFD解析により拡網力と抵抗を計算します。
このままでは、絞り込んだ64通りのオッターボードの拡網力と抵抗しか分かりません。
そのため、③で設計変数と目的変数の関係性を、近似式で表せるように処理します。
これを応答曲面法といいます。
最後に、③で構築した近似式を用いて、多目的最適化手法という手法を使用して最適解を探索しました。
この多目的最適化では、「ある程度妥協した設計」の候補をいくつか挙げることになります。
つまり、
「拡網力はとても大きいが、抵抗は普通のモデル」
「拡網力と抵抗のバランスをとったモデル」
「拡網力は普通だが、抵抗は小さいモデル」
といったように、複数候補を挙げるものが「多目的最適化」という手法です。
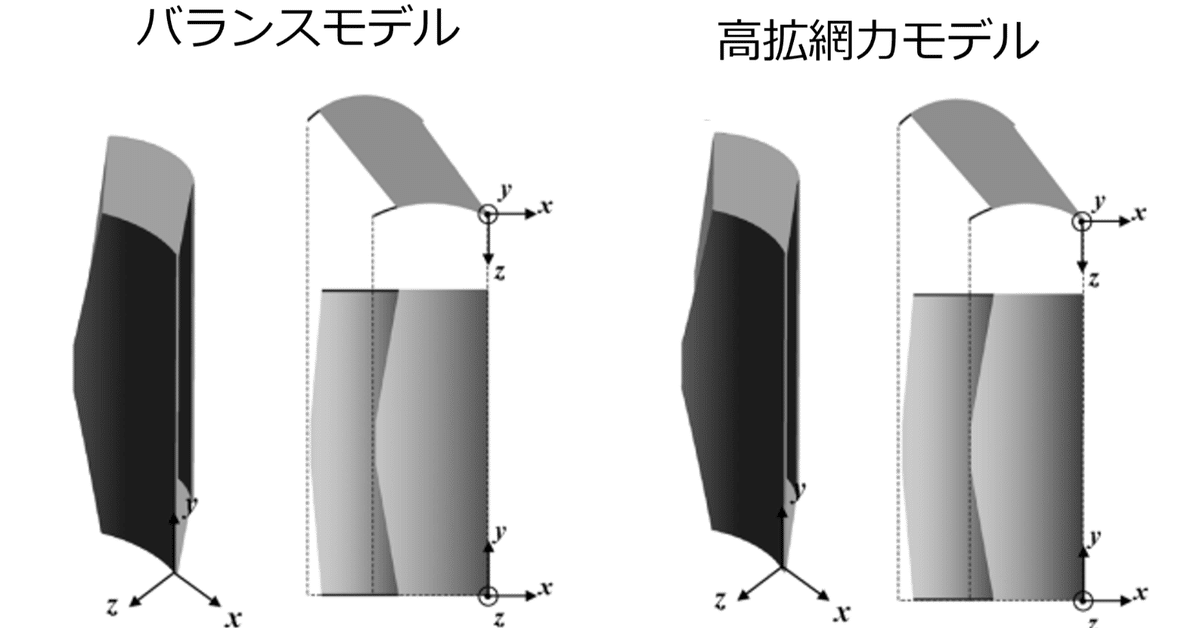
複葉型オッターボードの最適設計の結果
以下の図が、最適設計の結果です。
ここでは、以下の3つの最適設計の結果を取り上げます。
拡網力はとても大きいが、抵抗は普通のモデル:高拡網力モデル
拡網力と抵抗のバランスをとったモデル:バランスモデル
拡網力は普通だが、抵抗は小さいモデル:低抵抗モデル
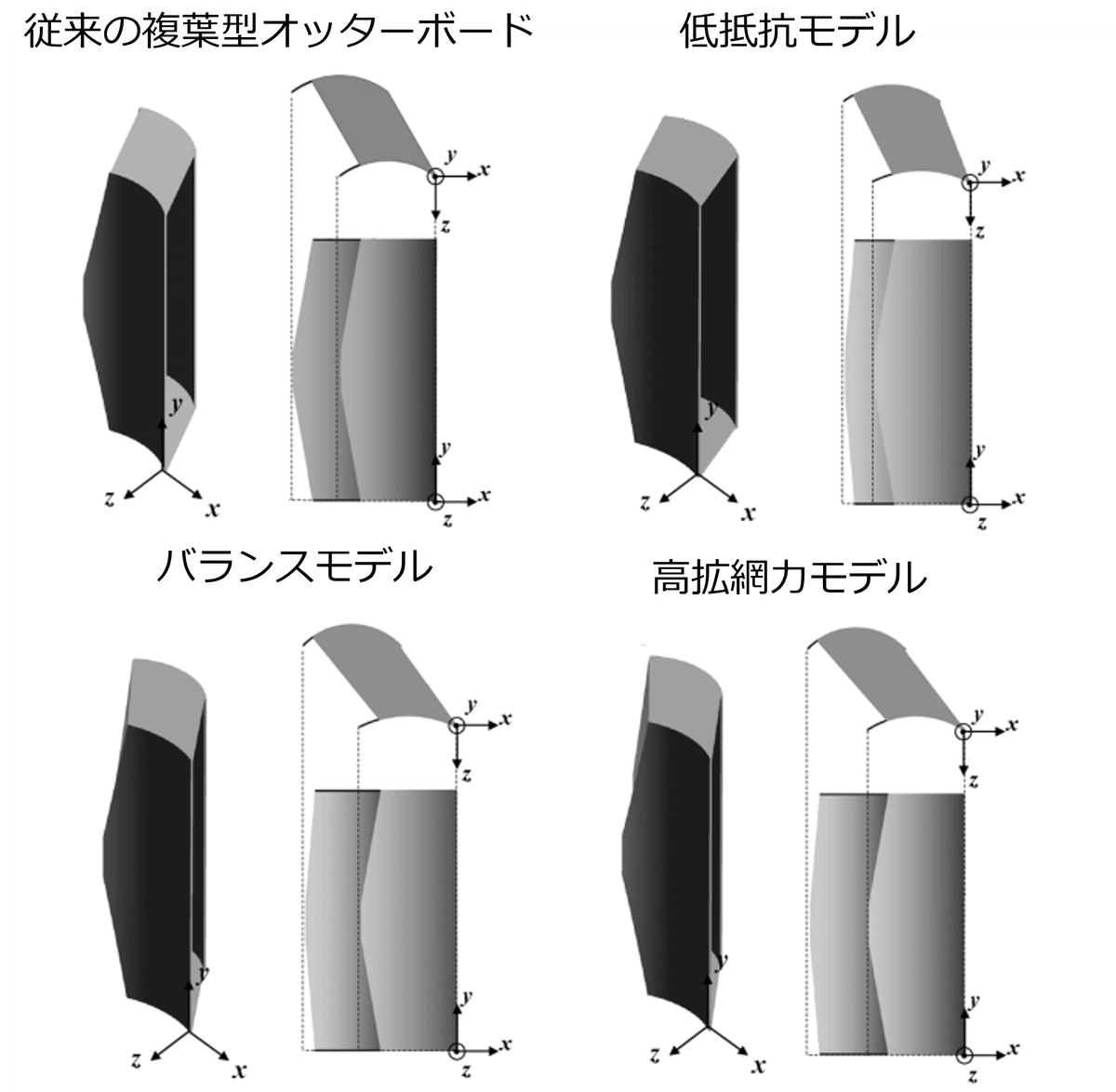
引用元:CFD解析を用いたオッターボードの形状最適化手法. 高橋勇樹, 藤森康澄, 胡夫祥, 木村暢夫日本水産学会誌 83(6) 950-960 2017年https://doi.org/10.2331/suisan.16-00076
それぞれの拡網力及び抵抗力は以下のようになりました。
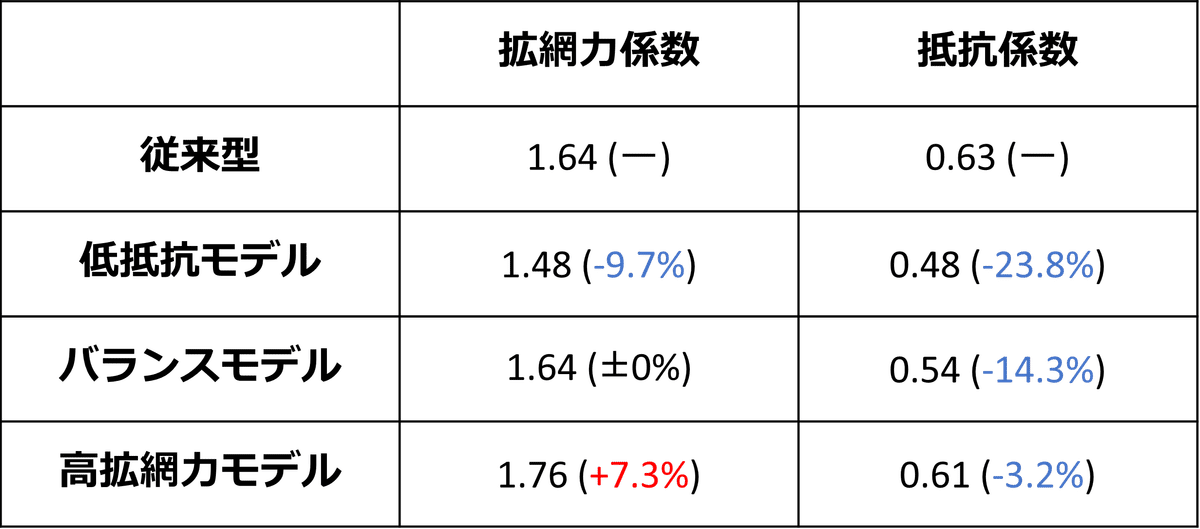
カッコ内の数値は、従来型との増減率を表す。
引用元:CFD解析を用いたオッターボードの形状最適化手法. 高橋勇樹, 藤森康澄, 胡夫祥, 木村暢夫日本水産学会誌 83(6) 950-960 2017年https://doi.org/10.2331/suisan.16-00076
まず、低抵抗モデルについては、拡網力は残念ながら従来型よりも低下してしまいました。
ただし、抵抗については、従来型と比較して2割以上削減できています。
バランスモデルについては、拡網力を維持しながら、抵抗を14.3%削減できています。
高拡網力モデルについては、拡網力を7.3%増加させると共に、抵抗についても従来型よりも若干抑えることができました。
このように、拡網力と抵抗が両方完璧な設計というのは難しいのですが、少なくとも従来型と比較して一定の改善が見られたものと考えています。
研究を終えて
上記の研究で、複葉型オッターボードを例にして、オッターボードの最適設計を試みました。
この最適化の一連の流れは、車や飛行機の設計では、既に用いられているものになります。
ただ、この論文発表時点では、漁具に対して適用した事例は少なかったものと思います。
ただ、ここで最大の問題は「実際の漁業でオッターボードを使用したときにはどの形状がベストなのか?」ということかと考えます。
これに対しては、まだ答えは出ていません。
というのは、漁業者によっては使用する網のサイズや設計が異なってくるため、必然的に必要となる拡網力も異なってきます。
ただ、例えば
「最低このぐらいの拡網力が必要で、その上で抵抗をできるだけ小さくしたい!」
というような際に、この手法が役に立つと考えています。
