
【経済的自立へ向けて】高配当企業の株価データ分析 その11:関係は1つの数字で表現できる
※登場する株式会社は全て架空の会社です。
前回の宿題は、
「関係の深さ、浅さを分かりやすく表現する方法がないでしょうか?」
でした。
関係をみるための鉄則は、散布図を書くことです
以下は、東京の気温と株式会社サマーの株価を2軸にとった散布図です。
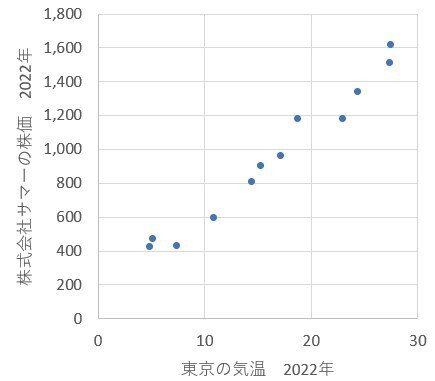
おーこれは、きれいに正比例してますね。
次にこちらは、東京の気温と株式会社ウィンターの株価を2軸にとった散布図です。

こちらは、きれいに半比例してますね。
関係には2種類あり、1つ目が正比例、2つ目が半比例です。
そして、どちらも、直線に近ければ近いほどその関係が深いということになります。
最後は、東京の気温と株式会社フォーシーズンズの株価を2軸にとった散布図です。

こちらは雲のようですね。気温と株価にほとんど関係がないことが分かります。
これらの関係の深さ、浅さを表現するためによい指標があります
それが、「相関係数」。
変動をみるための最も良い指標の名前が、変動係数 (忘れた人はこちら)
関係をみるための最も良い指標の名前が、相関係数
ここはそろっていていいですね。
相関係数は、以下の性質を持っています。
・-1から1までの値をとる
・絶対値が1に近いほど関係が深く、0に近いほど関係が浅い
先ほどのケースで言うと、
・2022年の東京の気温と株式会社サマーの相関係数が 0.98
・2022年の東京の気温と株式会社ウィンターの相関係数が -0.94
・2022年の東京の気温と株式会社フォーシーズンズの相関係数が 0.11
散布図をみた直感と合いますね。相関係数、便利じゃないか!
実際、実務上も本当に便利なんですよ。
次に、ここでよく質問が出るのが、
「いくつだと相関関係が強いんですか?」
です。
これは、諸説あるのですが、一般的には以下の解釈でよいと思います。
・相関係数の絶対値 0.7~1.0 強い関連性がある
・相関係数の絶対値 0.4~0.7 関連性がある
・相関係数の絶対値 0.2~0.4 弱い関連性がある
・相関係数の絶対値 0.0~0.2 関連性がない
ここで、大事なことは相関係数を数字としてきちんと確認することです。
よく新聞記事で以下のような記述があります。
2022年は東京の気温と株式会社フォーシーズンズの株価に正の相関がみられた。

直線を入れるだけで、なんとなく正の相関があるように見えてしまいます。しかし、先ほどみたように相関係数は0.11で、この2つの変数の間に関連性はありません。
こういった相関詐欺にだまされないように、きちんと相関係数を数字でみるようにしましょう。
それでは、相関係数さえみてれば大丈夫なのか?
残念ながら、それはそうでもないんです。
次回そのあたり深堀いたします。
今日は統計の授業っぽい感じになりましたが、あくまでこの関係編の目的は、「2つの株を組み合わせて劇的にリスクを下げる方法」を教授することです。その目的には少しずつ近づいているので安心してくださいね。
それでは、See you next time!
※次の記事へ行く場合はこちら ↓
※関係編の最初の記事に行きたい人はこちら ↓
※変動編から見たい人はこちら ↓
