
永久機関は可能か
エントロピー
エントロピーは物理学における熱力学と統計力学で特に使われている。

熱力学におけるエントロピー
エントロピーは系の「乱雑さ」や「無秩序さ」を表す量で、熱力学第二法則によれば孤立系のエントロピーは常に増大するか一定に保たれる。これは、自然界のプロセスが不可逆的であることを示していて、熱が高温から低温へと自然に移動するのはエントロピーが増大する方向だ。
統計力学におけるエントロピー
ある系が取り得る微視的な状態の数が多いほどその系のエントロピーは高くなる。ルートヴィッヒ・ボルツマンはこの関係を数式で表し、エントロピー ( S ) を次のように定義した。
S=kBlnW
( k_B ) はボルツマン定数、( W ) は系の取り得る微視的状態の数。
▼エントロピーの具体例▼
氷が溶ける:
氷が水に変わるときに分子の運動が活発になりエントロピーが増加する。
コーヒーにミルクを混ぜる:
ミルクが均一に混ざることでエントロピーが増加する。

エントロピーは情報理論にも応用され、情報の「不確実性」や「乱雑さ」を測る尺度としても使われている。
マクスウェルの悪魔の否定
マクスウェルの悪魔とは、1867年にスコットランドの物理学者ジェームズ・クラーク・マクスウェルが提唱した思考実験で、この思考実験では分子の動きを観察し特定の条件下でエントロピーを減少させることができる架空の存在を想定している。
気体が入った容器を仕切る小さな扉を操作し、速い分子だけを一方の部屋に、遅い分子だけをもう一方の部屋に移動させることで温度差を作り出す。これにより熱力学第二法則に反するような現象が起こるとされている。

しかし、一見して当たり前に冷やすという行為によって熱量が減少しているようにみえるが、例えば冷蔵庫でものを冷やすといった行為はそれを感じるものだが、それは自然な状態ではあり得なかった現象であるし、その冷却装置は必ず熱を帯びる。
熱は熱力学第二法則によって一定の値へ移動し、孤立系のエントロピーは常に増大するか一定に保たれるとされていた。例えば老いはあっても若返ることは実質無いように、若く見えることはあってもその老いは間違いなく進んでいる。
情報理論からも否定
マクスウェルの悪魔の否定は情報理論からも否定されている。それは実際には情報処理にもそれに伴うエネルギー消費があるため、その全体のエントロピーは増加している為だ。
情報を得るにもエネルギーが必要
その情報は一見して実態が無いのだからそこには何も無いように感じられるが、例えばあなたが何かを確認するときに必ず人体を動かしそれを確認して思考する。それらの動きは全てエネルギーの一種であって『無』ではなく、情報の取得には必ずエネルギーが消費されている。
その目で見る行為も、手に取る行為も、思考する行為も、その全てに対してエネルギーが発生する。朝起きて辺りを見渡して目覚ましを止める、これはその情報から得たものであって、だからこそ情報という存在はそこに無くともそれを得る為に必要なエネルギーが必要であるが故に、マクスウェルの悪魔の否定がされた訳だ。
ランダウア限界
ランダウア限界(Landauer’s limit)は、情報処理におけるエネルギー効率の理論的な下限を示す概念で、1961年にロルフ・ランダウアーによって提唱された。
E=kTln2
( k ) はボルツマン定数、( T ) は絶対温度。
情報を消去するためには必ずエネルギーが必要であり、これは熱力学第二法則に基づいている。
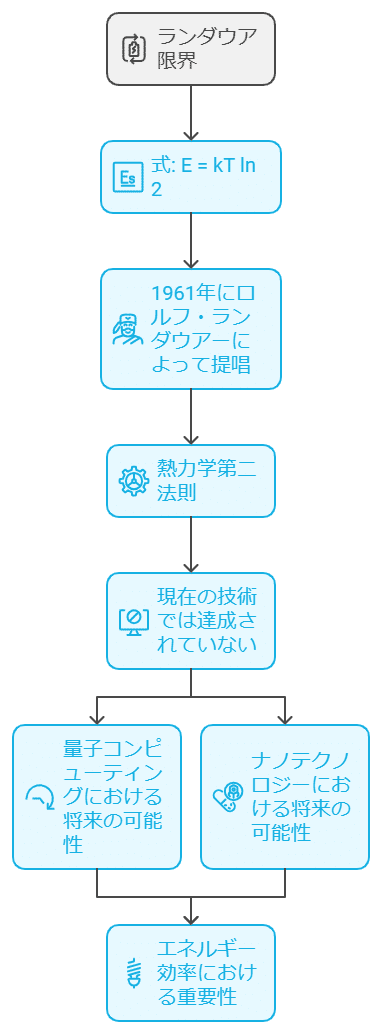
▲とにかく消費を抑えながらもその最低値を探りながら他に与える影響に対しての最高値を求める、というもの。
エントロピー、マクスウェルの悪魔、ランダウア限界、とここまでが一応の結論となっていて、まだ可能性の範囲、つまりは現実化はされていないが、熱力学第二法則に基づいてここへの到達が今後可能になると殆どエネルギーを消費せずに大きなものが生み出せれる。
現在ではこれが理想で目標とされている。
永久機関は可能か
量子力学の分野では、非常に効率的なエンジンやデバイスの開発が進められている。

量子エンジン
沖縄科学技術大学院大学(OIST)では量子エンジンの研究が行われており、量子効果を利用して高効率なエネルギー変換を目指している。しかし、これらのエンジンも外部からのエネルギー供給が必要であり永久機関とは異なる。
時間結晶
外部からエネルギーを供給し続けることで周期的に変化する状態を維持することができるというもの。しかし、これもエネルギー供給が必要であり、永久機関とは言えない。
情報とエネルギーは同じ概念
例えば火はそこにあるだけではエネルギーではなく、何かしらの影響を与える環境に持っていってから使用して初めてエネルギーとなる。
情報は今ある既存の情報によって様々なものの仕組みを知れたりもするが、遥か昔の時代からすればそれにすら興味がなかったのであるからその今ある既存の情報はその昔の時代の人達からすれば無である。
つまりはそこに活用が入って初めて有になるということ。
そう考えれば情報はある種エネルギーにもなるという理屈から、物質=エネルギーというものにひとつ足して、物質=エネルギー=情報、ということが成り立つ。

情報があるからそれを実現させようとするし、だからこそ物質に影響を与えてエネルギーとなる、この流れからある意味では無という存在から有に対してアプローチが出来るのだから、ランダウア限界からその下限に等しいものからそれ以上のエネルギーを発生させることが出来るともいえる。
永久機関という意味合いでは無いにしても、それはある意味ではそれに等しいものである。
PCの処理技術はランダウア限界からみると100万倍以上のコストがかかっている、つまりは極論100万分の1までコストを下げることが可能ということでもある。勿論それは理想であって実質的には不可能だけども、それに近いもの、例えば100分の1までに下げれればかなりの期待値がある。
スマートフォンの充電 :
ここに下限の限界点まで辿り着ければ、1時間の充電で半日持つのなら100万倍の時間を持たせることが可能になる。これは50万日という莫大な時間だ。
電気自動車 :
半日の充電で100㎞走れるのなら限界点は1億㎞まで走れることになる。
電気代 :
月平均2万円ならそれを100万分の1にまで抑えれる、これは実質無料だ。
◇
|最後に….。
永久機関の実現は熱力学第二法則から実現不可能だが、それに近い要素には入ることが可能だ。その実現は2070年には到達するのではと予想されているが、どうなるかはまだまだわからない。
大体の歴史からみるに、そのシンギュラリティの話題は繰り返されながら実現されていないようにみえるが、事実としてこの100年だけを見ても相当な進歩をみせている。
電卓の開発がされた当初は数学が終わると言われ、電話がプッシュフォンになれば自宅で計算ができると言われ、FAXができれば手紙が不要になるとされた。
勿論数学は終わっていないし、プッシュフォンで計算なんてしない。
しかしそれは大袈裟に言っているようにみえて事実として電卓によって計算の必要性は下がったし、プッシュフォンによって黒電話を回すことなく使用でき且つ携帯してネットにも繋がりながら計算もできる、手紙もどんどん進化してはメールにもなった。
何が言いたいのかというと、実現可能なレベルでの気づかない形として入ってくる要素がシンギュラリティという要素として今後入ってくるでしょう、と考えられるということだ。
何だったらその要素は我々が気づいていないだけで、もうすでにその要素に入っている最中なのかもしれない。
|以上….。
◇
