「Pythonではじめる異常検知入門」を寄り道写経 ～ 第５章「入出力の情報に基づくアプローチ」One-Class SVM

第５章「入出力の情報に基づくアプローチ」

書籍の著者　笛田薫 先生、江崎剛史 先生、李鍾賛 先生

---

この記事は、テキスト「Pythonではじめる異常検知入門」の第５章「入出力の情報に基づくアプローチ」の通称「寄り道写経」を取り扱います。
テキストは第５章から本格的な異常検知実装に入ります！

寄り道写経は One-Class SVM を用いた異常検知にトライします！
ではテキストを開いて異常検知の旅に出発です🚀

このシリーズは書籍「Pythonではじめる異常検知入門」（科学情報出版、「テキスト」と呼びます）の異常検知の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。

はじめに

---

テキスト「Pythonではじめる異常検知入門」のご紹介

テキストは、2023年4月に発売された異常検知の入門書です。
数式展開あり、Python実装ありのテキストなのです。
Jupyter Notebook 形式のソースコードと csv 形式のデータは、書籍購入者限定特典として書籍掲載のURLからダウンロードできます。

Pythonではじめる異常検知入門 ―基礎から実践まで― (エンジニア入門シリーズ117) | 笛田 薫, 江崎 剛史, 李 鍾賛 |本 | 通販 | Amazon

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonではじめる異常検知入門－基礎から実践まで－」初版、著者 笛田薫／江崎剛史／李鍾賛、オーム社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

かわいいフリー素材集

第５章 入出力の情報に基づくアプローチ

---

Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。

テキストのこの章では、「ホテリングの$${T^2}$$法」「$${k-}$$近傍法」「One-Class SVM」の基礎知識を習得して、One-Class SVMによる異常検知をPythonで実践することに取り組みます。

テキスト前半の基礎知識ゾーンは数値例の掲載がなく、寄り道しにくかったので、ひとまずスルーしました。
（時間があったら、いつか$${k}$$近傍法の異常検知にトライしたいです）

テキスト後半の One-Class SVM の異常検知「図5-4」について、ちょいと寄り道写経を行います！

インポート

### インポート

# 数値・確率計算
import pandas as pd
import numpy as np

## One-Class SVM
from sklearn.svm import OneClassSVM

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

Google Colab をご利用の場合は「描画」箇所を以下のように差し替えてください。

!pip install japanize_matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

5-3 特定の構造から外れたデータの検知：One-Class SVM

テキスト図5-4の「One-Class SVMによる異常データの検知」の描画に取り組みます。

■ データの作成
それぞれ独立に正規分布に従う２つの正規分布乱数$${x,y}$$を生成します。
乱数生成関数はテキストの関数を参考にさせていただき、作成しました。
なお、生成データの各値はテキストと異なります。

### データの作成

## 設定
# データ数
n_data = 200
# 乱数シード
seed = 1234

## データ作成関数関数の定義 テキストの関数を改造
def generate_data(n_data):
    df = pd.DataFrame()
    rng = np.random.default_rng(seed=seed)
    df['x'] = rng.normal(loc=50, scale=10, size=n_data) # 平均50, 標準偏差10
    df['y'] = rng.normal(loc=50, scale=10, size=n_data) # 平均50, 標準偏差10
    return df

## データ作成の実行
data = generate_data(n_data)

## データ概要の表示
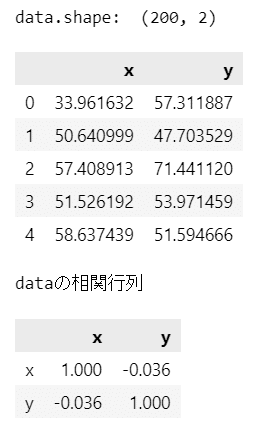
print('data.shape: ', data.shape)
display(data.head())
print('dataの相関行列')
display(data.corr().round(3))

【実行結果】
200個のサンプルです。
$${x}$$と$${y}$$の間に相関はほぼ無さそうです。

データができたのでシミュレーションに移りましょう！
なお、テキストのコードをそのまま用いて作成したデータを使うと、テキストと同値の図が描画できると思います。

■ One-Class SVMによる異常検知シミュレーション
One-Class SVM のパラメータ値をいろいろ変えて、シミュレーションしましょう。

シミュレーション関数を定義します。
以下のコードはテキストのコードを参考にさせていただき、シミュレーションのしやすさ、図の色付け、繰り返し処理の導入の点の変化を寄り道写経いたしました。

### One-Class SVM による異常検知シミュレーション関数の定義

def sim_one_class_svm(nus, gammas, lim=(20, 82)):

    ## 等高線の平面x軸・y軸の値の取得
    xx, yy = np.meshgrid(np.linspace(0, 100, 1000), np.linspace(0, 100, 1000))

    ## 描画処理
    # 描画領域の指定
    fig, ax = plt.subplots(1, 3, figsize=(12, 4.5))
    # ３つのOne-Class SVMを実行して描画
    for i, (gamma, nu) in enumerate(zip(gammas, nus)):
        
        ## One-Class SVMの実行
        # One-Class SVM分類器の設定
        clf = OneClassSVM(kernel='rbf', gamma=gamma, nu=nu)
        # 分類器の学習実行
        clf.fit(data)
        # 学習データで予測実行
        pred = clf.predict(data)
        # 学習済み分類器を用いて等高線データの作成
        zz = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
        zz = zz.reshape(xx.shape)

        ## 描画処理
        # 等高線の描画
        ax[i].contour(xx, yy, zz, levels=1, linewidths=1, colors='tab:red',
                    linestyles='--')
        # 等高面の描画
        ax[i].contourf(xx, yy, zz, levels=1, colors=['lightblue', 'lightpink'],
                    alpha=0.2)
        # 正常データの散布図の描画 正常データは予測値pred==1
        sns.scatterplot(x=data['x'].loc[np.where(pred == 1)],
                        y=data['y'].loc[np.where(pred == 1)],
                        color='tab:blue', edgecolors='white', s=40, ax=ax[i])
        # 異常データの散布図の描画 異常データは予測値pred==-1
        sns.scatterplot(x=data['x'].loc[np.where(pred == -1)],
                        y=data['y'].loc[np.where(pred == -1)],
                        color='tomato', edgecolors='tab:red', alpha=0.7,
                        s=80, ax=ax[i])
        # 修飾
        ax[i].set(xlabel=r'$x_1$', ylabel=r'$x_2$', xlim=lim, ylim=lim,
                title=rf'$\nu$={nu}, $\gamma=${gamma}')
    # 全体修飾
    fig.suptitle('One-Class SVM による外れ値の検出: 赤い点は外れ値', fontsize=16)
    plt.tight_layout();

ではシミュレーションの開始です。
２つのパラメータ$${\nu, \gamma}$$の値をいろいろ変えてみて、正常と異常の境界線「判別境界」の移り変わりを楽しんでください！！！

【パラメータ】
$${\boldsymbol{\nu}}$$（nu）：
・異常データの割合
・テキストは「5%」を設定
$${\boldsymbol{\gamma}}$$（gamma）：
・決定境界の複雑さを制御するrbf カーネルのパラメータ
・テキストは「0.0001, 0.001, 0.01」を設定

最初にテキストと同じパラメータ値で実行します。

### シミュレーションの実行

# パラメータ設定
nus = [0.05, 0.05, 0.05]        # ν：異常データの割合
gammas = [0.0001, 0.001, 0.01]  # γ：rbfカーネルの係数

# シミュレーション実行
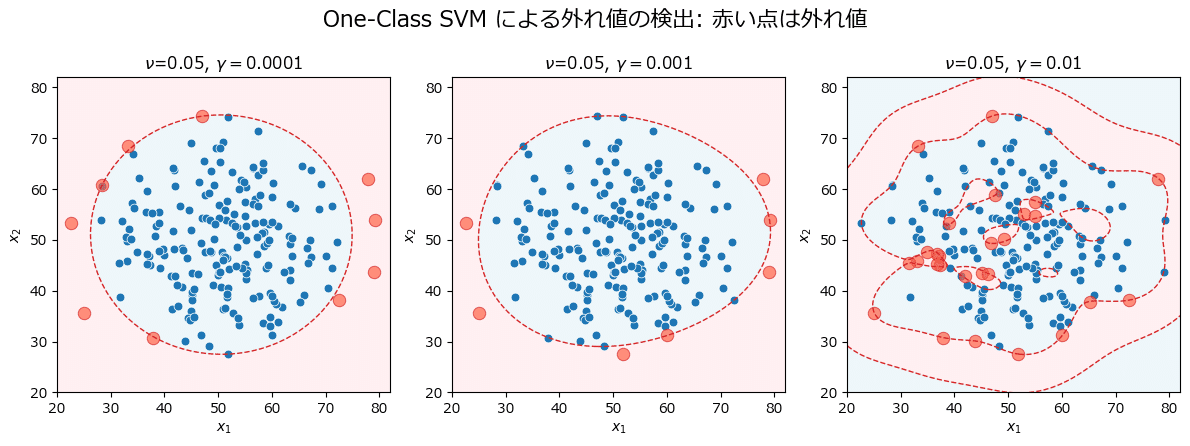
sim_one_class_svm(nus, gammas)

【実行結果】
赤い点線が判別境界、青い領域が正常、赤い領域が異常です。
パラメータ$${\gamma}$$（gamma）の値によって判別境界が変わっていく様子が分かります。

続いてパラメータ$${\gamma}$$を変更します。

### シミュレーションの実行

# パラメータ設定
nus = [0.05, 0.05, 0.05]        # ν：異常データの割合
gammas = [0.001, 0.003, 0.005]  # γ：rbfカーネルの係数

# シミュレーション実行
sim_one_class_svm(nus, gammas)

【実行結果】
0.001～0.005に変化させて、判別境界が徐々に崩れていく（過学習していく）様子が分かります。

パラメータ$${\nu}$$を 10% に変えてみます。
パラメータ$${\gamma}$$はテキストと同じ値です。

### シミュレーションの実行

# パラメータ設定
nus = [0.1, 0.1, 0.1]           # ν：異常データの割合
gammas = [0.0001, 0.001, 0.01]  # γ：rbfカーネルの係数

# シミュレーション実行
sim_one_class_svm(nus, gammas)

【実行結果】
異常値の数が増えました。

シミュレーションは楽しいですね！
シミュレーションも参考にしつつ、 One-Class SVM のパラメータを決定して「異常度の閾値」が定まると、未知データに対する異常検知ができそうです！

アディショナルタイム！

未知データを作成して異常検知を試してみましょう！

① 可視化関数の作成
ひとまず可視化の関数を作成します。

### 正常・異常を識別する散布図の描画関数

def plot_anomaly_detection(pred, score, thres, ylabel):
    
    ## 描画用のx軸の値の作成
    x = np.arange(1, len(pred)+1)

    ## 描画
    # 描画領域の設定
    plt.figure(figsize=(7, 4))
    # 正常データの散布図の描画
    sns.scatterplot(x=x[(pred == 1)], y=score[pred == 1], color='tab:blue',
                    label='正常')
    # 異常データの散布図の描画
    sns.scatterplot(x=x[(pred == -1)], y=score[pred == -1], s=80, color='tomato',
                    ec='white', alpha=0.7, label='異常')
    # 判別境界=0の水平線の描画
    plt.axhline(thres, color='tab:red', ls='--', label='閾値')
    # 修飾
    plt.xlabel('データ番号')
    plt.ylabel(ylabel)
    plt.legend(bbox_to_anchor=(1, 1))
    plt.grid(lw=0.5)
    plt.show()

② 異常検知モデルの構築
One-Class SVM を200個の学習データで学習して、異常検知モデルを作ります。
学習データの 5% を異常として扱う閾値を設定しましょう。
異常データの割合パラメータ：$${\nu=0.05}$$にします。
また、決定境界の複雑さパラメータ：$${\gamma=0.0001}$$にします。
「clf」が異常検知モデルです。

### 異常検知のためのOne-Class SVM分類器の学習と正常・異常の分類実行
# One-Class SVM分類器の設定
clf = OneClassSVM(kernel='rbf', gamma=0.0001, nu=0.05)
# 分類器の学習実行
clf.fit(data)
# 学習データの正常・異常の分類実行
pred = clf.predict(data)

【実行結果】なし

③ 学習データを用いた異常検知の可視化
では、判別境界からの距離を異常の判断材料＝異常度にして、正常・異常の可視化をします。
decision_function でデータ点と判別境界の距離を算出します。
正常の場合は距離の値が正、異常の場合は距離の値が負です。

### 判別境界からの距離に基づく正常・異常の可視化

# 学習データの判別境界からの距離の算出 
dist = clf.decision_function(data)
# 描画
plot_anomaly_detection(pred, dist, 0, '判別境界からの距離')

【実行結果】
200個のデータのうち10個を異常と判断する異常検知分類器ができました！

score_samples で算出できるスコアも異常検知に利用できます。
この場合の判別境界＝閾値は offset_ で取得できます。
さっそくスコアの可視化をしてみましょう。

### スコアに基づく正常・異常の可視化

# スコアと判別境界（閾値）の算出 
score = clf.score_samples(data)
thres = clf.offset_
# 描画
plot_anomaly_detection(pred, score, thres, 'スコア')

【実行結果】
距離に基づく異常検知と同じ結果になります（当たり前！？）

④ 未知データの作成
異常検知モデルの概要が分かったところで、未知データを作成して異常検知をしてみましょう。

### 未知データの異常検知

# 未知データの作成
data_new = np.array([[20, 20], [30, 30], [40, 40], [50, 50], [60, 60], [70, 70],
                      [80, 80]])
print('未知データ')
print(data_new)

【実行結果】
７個の未知データです。

⑤ 未知データの異常検知の実行
準備が整いましたので、いよいよ異常検知を行います！
異常検知モデル clf を用いて未知データの異常検知を実行します。

### 未知データの異常検知：正常・異常の分類予測
pred_new = clf.predict(data_new)
print('異常検知（-1が異常）')
print(pred_new)

【実行結果】
１番目・２番目・６番目・７番目のデータが異常判定となりました！

７個のデータの正常・異常の可視化をしましょう。
まず距離に基づく分類から。

### 未知データの異常検知：判別境界からの距離で異常度をはかる
# 判別境界からの距離の算出
dist_new = clf.decision_function(data_new)
# 描画
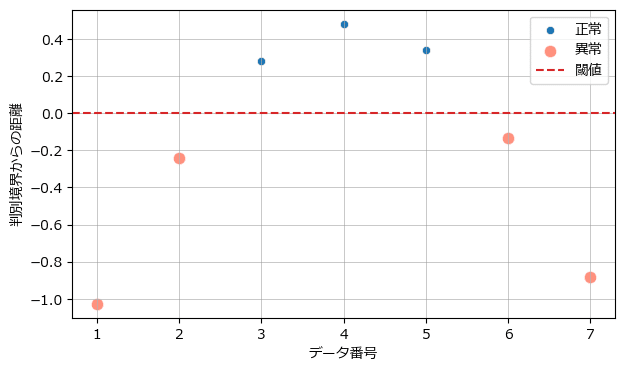
plot_anomaly_detection(pred_new, dist_new, 0, '判別境界からの距離')

【実行結果】
放物線のようです。

次はスコアによる分類の可視化です。

## 未知データの異常検知：スコアで異常度をはかる
# スコアと閾値の算出
score_new = clf.score_samples(data_new)
thres_new = clf.offset_
# 描画
plot_anomaly_detection(pred_new, score_new, thres_new, 'スコア')

【実行結果】

One-Class SVM による異常検知を堪能できました！

第５章の寄り道写経は以上です。

---

シリーズの記事

次の記事

前の記事

目次

ブログの紹介

---

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは Ｒ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経 ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。