
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第4章4.3「相関係数の標本分布と信頼区間」
第4章「母数の推定のシミュレーション」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第4章「母数の推定のシミュレーション」4.3節「相関係数の標本分布と信頼区間」、4.4節「演習問題」の Python写経活動 を取り扱います。
今回はシミュレーションを通じて相関係数の信頼区間とお友達になります。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
4.3 相関係数の標本分布と信頼区間
私にとって難易度の高い節です。
標本相関係数の標本分布を学び、母相関係数の信頼区間を3つの方法で深堀りします。
今回取り組んだ非心t分布は今後の章でも頻出しますので、好きになっておきたいテーマです!
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# データフレーム
import pandas as pd
# 確率・統計
import scipy.stats as stats
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
4.3節をざっくり要約
① 標本相関係数の変換
・統計量$${T}$$に変換:母相関係数が0のときに有効な変換
・Fisherの$${Z}$$変換
② 母相関係数の信頼区間
・Fisherの$${Z}$$変換:標本が2変量正規分布に従うことを仮定
・非心t分布:回帰分析の仮定を満たすことを仮定
・ブートストラップ法:母集団分布に仮定を置かない

4.3.1 標本相関係数 R の標本分布
統計量 T へ変換
標本相関係数$${R}$$をt分布と対応付ける目的で統計量$${T}$$に変換します。
条件は、相関係数が2変量正規分布に従う確率変数から求められていることです。
また、母相関係数$${\boldsymbol{\rho}}$$が0のときのみ、統計量$${\boldsymbol{T}}$$はt分布に従う点に注意が必要です。
テキストの数式をお借りします。
$$
T=\cfrac{R}{\sqrt{(1 - R^2) / (n - 2)}} = \cfrac{R}{\sqrt{1-R^2}}\ \sqrt{n-2}\ \sim t\ (n-2)
$$
統計量$${T}$$は自由度$${n-1}$$のt分布に従います。

■ 標本相関係数$${R}$$を$${T}$$に変換するシミュレーション
テキストに従い、母相関係数$${\rho}$$が$${-0.5, 0, 0.3}$$の3ケースで標本相関係数$${R}$$を$${T}$$に変換して、分布の形状を比較します。
シミュレーション回数は 10000 です。
### 161ページ ρ=0のときのみTが自由度n-2のt分布に従うことを確認 162ページ図4.21
## 設定と準備
mu_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
n = 20 # サンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
rhos = [-0.5, 0, 0.8] # 3つの母相関係数
# 描画領域の設定
plt.figure(figsize=(10, 7))
# 3つの母相関係数ごとに標本相関係数のシミュレーションを行い、結果を描画
for i, rho in enumerate(rhos):
## 相関行列の設定
rho_matrix = np.array([[1, rho],
[rho, 1]])
## シミュレーション
rng = np.random.default_rng(seed=7)
# 標本相関係数rの生成
r = np.array([np.corrcoef(
rng.multivariate_normal(
size=n, mean=mu_vec,
cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec)
).T)[0, 1]
for _ in range(iter)])
# t統計量の算出
t = r / np.sqrt((1 - r**2) / (n - 2))
## 結果
# 描画領域の追加
ax = plt.subplot(2, 2, i+1)
# tのヒストグラムの描画
ax.hist(t, bins=50, density=True, ec='white', alpha=0.7)
# t分布の確率密度関数の描画
line_x = np.linspace(t.min(), t.max(), 1001)
ax.plot(line_x, stats.t.pdf(line_x, df=n-2), linewidth=2, color='tab:red')
# x軸ラベル、y軸ラベル、タイトルの設定
ax.set(xlabel='t', ylabel='Density', title=rf'$\rho$={rho}')
plt.tight_layout();【実行結果】
赤い線は自由度$${n-2}$$のt分布です。
母相関係数$${\rho=0}$$のときのみ、標本相関係数のヒストグラムの形状とt分布の確率密度関数の形状が一致します。
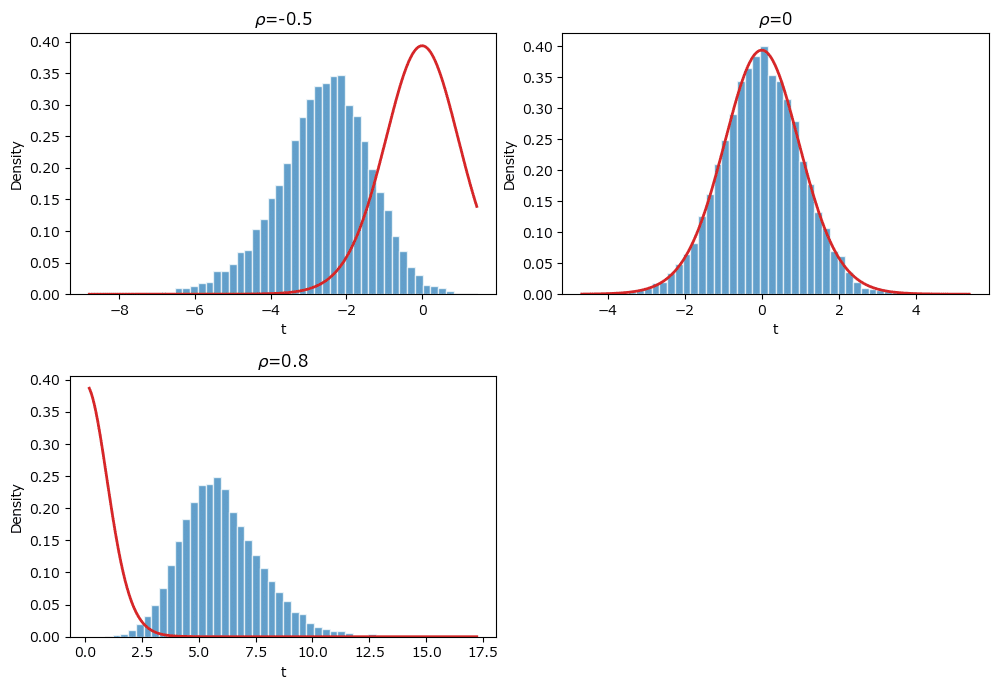
テキストは「この変換では$${\rho \neq 0}$$の場合に母相関係数$${\rho}$$の信頼区間を求められない」と締めくくっています。

Fisher の Z 変換(逆双曲線正接変換)
【利用する条件】
サンプルサイズ$${n}$$が大きいとき、2変量正規分布に従う確率変数同士の相関係数$${R}$$を Fisher の$${Z}$$変換した量は、近似的に標準正規分布に従います。
テキストによると、上記条件に合致する場合、次の式で表される Fisher の$${Z}$$変換(逆双曲線正接変換:$${\tanh^{-1}}$$)を行うことで、母相関係数$${\rho}$$の信頼区間を近似的に求められるそうです。
$$
Z = \cfrac{1}{2}\ \log\left(\cfrac{1+R}{1-R} \right)
$$
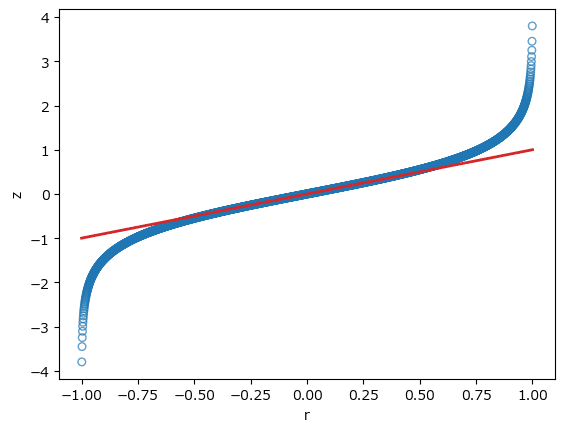
テキストに従って、$${-0.999 \leq R \leq 0.999}$$の相関係数を逆双曲線正接変換して可視化します。
R の atanh() の代わりに numpy の arctanh() 使用します。
### 163ページ -0.999≦R≦0.999の相関係数を逆双曲線正接変換 163ページ図4.22
# 相関係数rの数列の作成
r = np.arange(-0.999, 1.0, 0.001) # -0.999~0.999、0.001刻み
# Z変換(arcanh:逆双曲線正接関数)
z = np.arctanh(r)
# rとzの散布図(青い点)の描画
plt.scatter(r, z, s=30, ec='tab:blue', fc='None', alpha=0.7)
# y=xの直線(赤)の描画
plt.plot([-1, 1], [-1, 1], color='tab:red', linewidth=2)
# x軸ラベル、y軸ラベルの設定
plt.xlabel('r')
plt.ylabel('z');【実行結果】

■ 相関係数と変換と正規分布近似のシミュレーション
テキストの数式をお借りします。
母相関係数$${\rho}$$を 次の式のようにFisher の$${Z}$$変換した値を$${\eta}$$と呼びます。
$$
\eta = \cfrac{1}{2}\ \log\left(\cfrac{1+\rho}{1-\rho} \right)
$$
標本相関係数$${R}$$を変換した$${Z}$$は、サンプルサイズ$${n}$$が大きいときに、平均$${\eta}$$、標本偏差$${\sqrt{\frac{1}{n-3}}}$$の正規分布に近似的に従います。
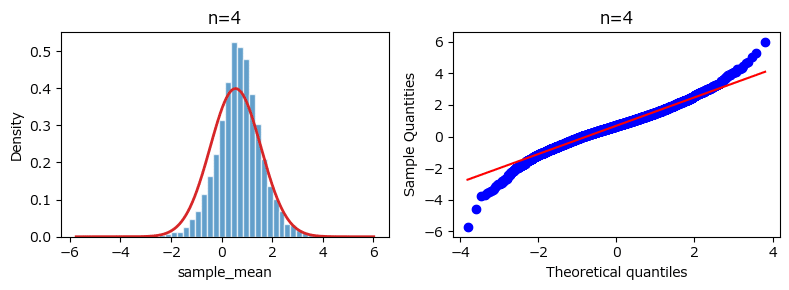
サンプルサイズ$${n=4, 20, 100}$$のときの標本相関係数から算出した$${Z}$$のヒストグラムが、上記の正規分布に近似的に従っていく様子をシミュレーションします。
### 163ページ 164ページ図4.23
## 設定と準備
n_list = [4, 20, 100] # 3つのサンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
rho = 0.5 # 母相関係数
mv_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
rho_matrix = np.array([[1, rho], # 相関行列
[rho, 1]])
## シミュレーション
rng = np.random.default_rng(seed=1234)
# 3つのサンプルサイズごとにシミュレーションと描画を繰り返し処理
for n in n_list:
## シミュレーション
# 標本相関係数rの生成
r = np.array([np.corrcoef(
rng.multivariate_normal(
size=n, mean=mu_vec,
cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec)
).T)[0, 1]
for _ in range(iter)])
# z変換
z = np.arctanh(r)
## 結果の描画
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# ヒストグラムの描画
ax1.hist(z, bins=50, density=True, color='tab:blue', ec='white', alpha=0.7)
# 正規分布の確率密度関数の描画
line_x = np.linspace(z.min(), z.max(), 1001)
ax1.plot(line_x,
stats.norm.pdf(
line_x, loc=np.arctanh(rho), scale=np.sqrt(1 / (n - 3))),
linewidth=2, color='tab:red')
# x軸ラベル・y軸ラベル・タイトルの設定
ax1.set(xlabel='sample_mean', ylabel='Density', title=f'n={n}')
# 正規Q-Qプロットの描画
stats.probplot(z, dist='norm', plot=ax2)
ax2.set(ylabel='Sample Quantities', title=f'n={n}')
# 修飾
plt.tight_layout()
plt.show()【実行結果】
赤い線は平均$${\eta}$$、標本偏差$${\sqrt{\frac{1}{n-3}}}$$の正規分布の確率密度関数です。
サンプルサイズが大きくなるにつれて、$${Z}$$が正規分布の確率密度関数に合っていく様子が分かります。
また右のQ-Qプロットでも、サンプルサイズが大きくなるにつれて正規分布に合っていく様子が分かります。



Fisher の Z 変換を用いた母相関係数の信頼区間
標本が2変量正規分布から生成されたことを仮定できる場合、Fisher の$${Z}$$変換を利用して母相関係数の信頼区間を算出できます。
テキストによると、サンプルサイズ$${n}$$が大きいとき、以下の区間内に$${Z}$$の取りうる値の約 95% が含まれることになります。
母相関係数$${\rho}$$を Fisher の$${Z}$$変換した$${\eta}$$の信頼区間です。
$$
Z - 1.96 \cfrac{1}{\sqrt{n-3}} \leq \eta \leq Z + 1.96 \cfrac{1}{\sqrt{n-3}}
$$
母相関係数$${\rho}$$の信頼区間は次のようになります。
$$
\tanh \left( Z - \cfrac{1.96}{\sqrt{n-3}} \right) \leq \rho \leq \tanh \left( Z + \cfrac{1.96}{\sqrt{n-3} }\right)
$$

■ Fisher の$${Z}$$変換で母相関係数の95%信頼区間をシミュレーション
テキストに従い、母相関係数$${\rho=0.5}$$、サンプルサイズ$${n=100}$$の2変量正規分布乱数を生成して95%信頼区間を算出するシミュレーションを20000回繰り返し、母相関係数が95%信頼区間に含まれる割合を求めます。
### 166ページ tanhで変換して95%信頼区間に含まれるかシミュレーション
## 設定と準備
rho = 0.5 # 母相関係数
eta = np.arctanh(rho) # FisherのZ変換
mv_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
n = 100 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
rho_matrix = np.array([[1, rho], # 相関行列
[rho, 1]])
## シミュレーション
rng = np.random.default_rng(seed=123)
# 標本相関係数rの生成
r = np.array([np.corrcoef(
rng.multivariate_normal(
size=n, mean=mu_vec,
cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec)
).T)[0, 1]
for _ in range(iter)])
# 信頼区間の実現値の下限
ci_lower = np.tanh(np.arctanh(r) - (1.96 / np.sqrt(n - 3)))
# 信頼区間の実現値の上限
ci_upper = np.tanh(np.arctanh(r) + (1.96 / np.sqrt(n - 3)))
# rhoが95%信頼区間に含まれる数をカウント
true_num = sum((ci_lower <= rho) & (rho <= ci_upper))
## 結果
true_num / iter # 信頼区間内に母相関係数が含まれる割合【実行結果】
約 95% の割合で母相関係数が95%信頼区間に含まれました!

■ mtcarsデータセットで母相関係数の95%信頼区間の実現値を計算
テキストにならい、R の標準データセットに含まれる「mtcarsデータセット」を用いて、燃費と車両重量の母相関係数の95%信頼区間の実現値を計算します。
statsmodels で R 標準データセットを読み込みます。
### R Datasetを取得するライブラリのインポート
import statsmodels.api as smデータセットを読み込みます。
### 167ページ mtcarsデータセットの読み込み ※statsmodelsでRのデータセットを読み込み
# mpg:燃費, wt:車両重量の母相関係数の95%信頼区間の実現値を計算する
mtcars = sm.datasets.get_rdataset(dataname='mtcars', package='datasets').data
print('mtcars.shape', mtcars.shape)
display(mtcars.head())【実行結果】
mpg:燃費と wt:車両重量を使用します。

母相関係数の95%信頼区間の実現値を計算します。
### 167ページ mtcarsの母相関係数の信頼区間の実現値の計算
r = mtcars[['mpg', 'wt']].corr().iloc[0, 1] # pandasで標本相関係数を算出
n = mtcars.shape[0] # 標本サイズ
# 標準正規分布の97.5パーセンタイル値。約1.96と判明しているが、厳密に求める
z_0975 = stats.norm.ppf(q=0.975, loc=0, scale=1)
# 信頼区間の算出と表示
print('95%信頼区間下限:', np.tanh(np.arctanh(r) - z_0975 / np.sqrt(n - 3)))
print('95%信頼区間上限:', np.tanh(np.arctanh(r) + z_0975 / np.sqrt(n - 3)))【実行結果】

★別解:scipy.stats の pearsonr を用いて95%信頼区間算出
### 169ページ 母相関係数の信頼区間 scipy.statsのpearsonrを使用
result = stats.pearsonr(mtcars.mpg, mtcars.wt)
print(result)
print(result.confidence_interval(confidence_level=0.95))【実行結果】
上段は標本相関係数、無相関検定のp値です。
下段は母相関係数の95%信頼区間です。

★別解:pingouin の corr を用いて95%信頼区間算出
### 番外編 pingouinのcorrで母相関係数の信頼区間を表示
import pingouin as pg
pg.corr(mtcars.mpg, mtcars.wt)【実行結果】
r:標本相関係数、CI95%:母相関係数の95%信頼区間です。

■ 非2変量正規分布から生成された標本のシミュレーション
Fisher の$${Z}$$変換を利用した母相関係数の信頼区間の計算は、標本が2変量正規分布から生成されたことを仮定しています。
2変量正規分布で無い分布として「2変量t分布」から標本が生成される場合に、Fisher の$${\boldsymbol{Z}}$$変換後の相関係数が正規分布に近似しないことをシミュレーションで確かめます。
2変量t分布乱数は scipy.stats の multivariate_t を用いて、rvs で乱数生成しています。
### 168ページ 2変量t分布(=非正規分布)のシミュレーション 169ページ図4.24
# 2変量t分布の乱数生成はscipy.stataのmultivariate_tを使用
## 設定と準備
rho = 0.5 # 母相関係数
mv_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
nu = 4 # 自由度
rho_matrix = np.array([[1, rho], # 相関行列
[rho, 1]])
n = 1000 # サンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
## シミュレーション
# 標本相関係数rの生成
np.random.seed(123) # scipyの乱数シードはnumpyで指定する
r = np.array([np.corrcoef(
stats.multivariate_t.rvs(
size=n,
loc=mu_vec,
shape=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec),
df = nu,
).T)[0, 1]
for _ in range(iter)])
# z変換
z = np.arctanh(r)
## 結果
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
# ヒストグラムの描画
ax1.hist(z, bins=50, density=True, color='tab:blue', ec='white', alpha=0.7)
# 正規分布の確率密度関数の描画
line_x = np.linspace(z.min(), z.max(), 1001)
ax1.plot(line_x,
stats.norm.pdf(
line_x, loc=np.arctanh(rho), scale=np.sqrt(1 / (n - 3))),
linewidth=2, color='tab:red')
# x軸ラベル・y軸ラベル・タイトルの設定
ax1.set(xlabel='sample_mean', ylabel='Density', title=f'n={n}')
# 正規Q-Qプロットの描画
stats.probplot(z, dist='norm', plot=ax2)
ax2.set(ylabel='Sample Quantities', title=f'n={n}')
# 修飾
fig.suptitle('標本相関係数 $R$ をFisherの $Z$ 変換した量の標本分布\n'
'(母集団が2変量t分布のとき)')
plt.tight_layout()
plt.show()【実行結果】
確かに正規分布に近似していません。


4.3.2 非心t分布を用いた母相関係数の信頼区間
非心t分布、非心度・・・
パワーワードいただきました!
相関係数の推定は難解ですね~。
非心t分布を用いて母相関係数の信頼区間を計算できる条件です。
テキストの1文を引用いたします。
2変量正規分布の仮定を満たされなくても、「一方の変数の値によらず、他方の変数の値が、分散の等しい正規分布に従って分布している」と仮定できるなら、非心t分布を用いた母相関係数の信頼区間を計算できます。
テキストは単回帰分析と照らし合わせて、相関係数と非心t分布の関係を紐解きます。
ひとまずテキストの図4.25(回帰分析説明用の散布図)を描画します。
### 170ページ 図4.25
## 設定
a = 1 # 切片
b = 1.5 # 傾き
n = 30 # 値1~5の数
## データ作成(データフレームに変数を1つずつ追加)
# 乱数の設定
rng = np.random.default_rng(seed=0)
# データフレームに変数xを作成: 1~5の値を30ずつ設定
dat = pd.DataFrame({'x': np.repeat(a=range(1, 6), repeats=n)})
# 変数xdammyを追加: 連続一様分布
dat['xdammy'] = rng.uniform(size=n*5, low=dat['x'].min(), high=dat['x'].max())
# 変数yを追加: a + b * x + ノイズ
dat['y'] = a + b * dat['x'] + rng.normal(size=n*5, loc=0, scale=2)
# 変数ydammyを追加: a + b * xdammy + ノイズ
dat['ydammy'] = a + b + dat['xdammy'] + rng.normal(size=n*5, loc=0, scale=2)
## 散布図の描画
# xとyの散布図の描画
plt.scatter(dat['x'], dat['y'], color='tab:blue', ec='white', alpha=0.7)
# xdammyとydammyの散布図の描画
plt.scatter(dat['xdammy'], dat['ydammy'], color='tab:blue', alpha=0.2)
# 切片a、傾きbの直線の描画
plt.plot([0.8, 5.2], [a+b*0.8, a+b*5.2], color='tab:red')
# 修飾
plt.xlabel('x')
plt.ylabel('y');【実行結果】


■ 統計量$${T}$$、非心度$${\lambda}$$、非心t分布
「一方の変数の値によらず、他方の変数の値が、分散の等しい正規分布に従って分布している」という回帰分析における仮定が相関係数において成り立つとき、次の統計量$${T}$$は自由度$${n-2}$$、非心度$${\lambda = \frac{\rho}{\sqrt{(1-\rho^2)/n}}=\frac{\rho}{\sqrt{1-\rho^2}}}$$の非心t分布に従います。
$$
T=\cfrac{R}{\sqrt{(1 - R^2) / (n - 2)}} = \cfrac{R}{\sqrt{1-R^2}}\ \sqrt{n-2} \\
$$
非心t分布、、、何者でしょう???
テキストは非心度を「母数と、母数に関する研究者の仮説が一致しないことに由来するずれ」を指すと説明します。
「4.3.1 標本相関係数 R の標本分布」の統計量$${T}$$へ変換の箇所で相関係数のヒストグラムとt分布を重ね描きして「$${\rho \neq 0}$$のとき、ずれる」ことを可視化しました。
非心度t分布を使うと、$${\rho \neq 0}$$の場合もずれないことになるそうです。
シミュレーションします!

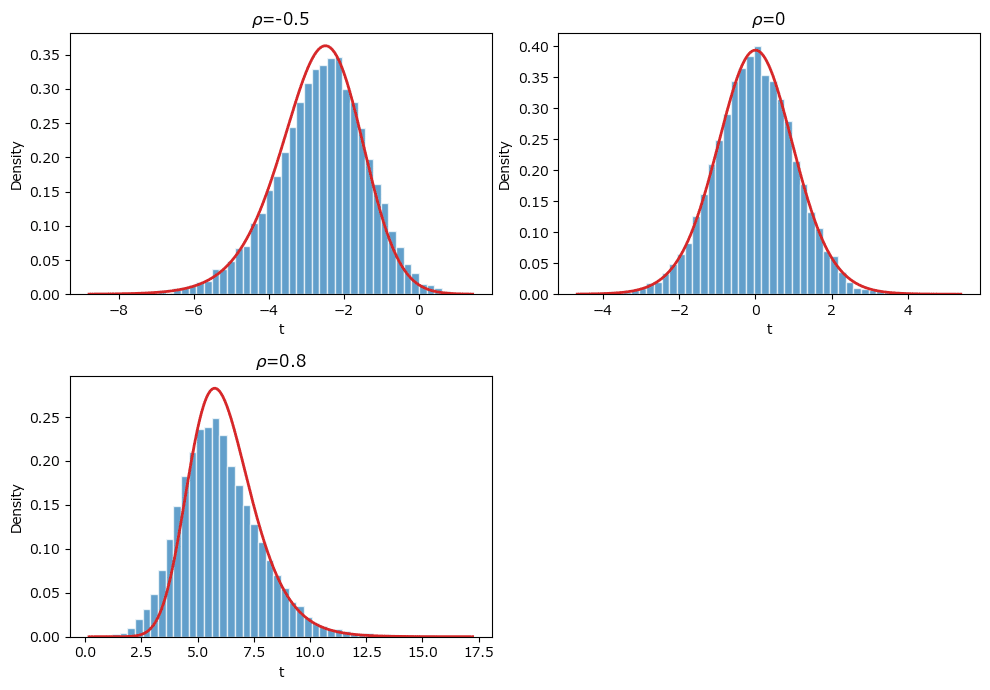
■ 標本相関係数$${R}$$を$${T}$$に変換して非心t分布と比べるシミュレーション
母相関係数$${\rho=-0.5, 0, 0.8}$$の3ケースのシミュレーションです。
非心t分布には scipy.stats の nct を利用します。
引数 nc に非心度$${\lambda}$$を設定します。
### 171ページ ρ≠0のTの標本分布を自由度n-2の非心t分布に重ね合わせる 172ページ図4.26
## 設定と準備
rhos = [-0.5, 0, 0.8] # 3つの母相関係数ρ
mu_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
n = 20 # サンプルサイズ
iter = 10000 # 標本を得る回数(標本数)
# 描画領域の設定
plt.figure(figsize=(10, 7))
# 3つの母相関係数ごとに標本相関係数のシミュレーションを行い、結果を描画
for i, rho in enumerate(rhos):
## 相関行列の設定
rho_matrix = np.array([[1, rho],
[rho, 1]])
## シミュレーション
rng = np.random.default_rng(seed=7)
# 標本相関係数rの生成
r = np.array([np.corrcoef(
rng.multivariate_normal(
size=n, mean=mu_vec,
cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec)
).T)[0, 1]
for _ in range(iter)])
# t統計量の算出
t = r / np.sqrt((1 - r**2) / (n - 2))
## 結果
# 描画領域の追加
ax = plt.subplot(2, 2, i+1)
# tのヒストグラムの描画
ax.hist(t, bins=50, density=True, ec='white', alpha=0.7)
# 非心t分布の確率密度関数の描画 scipy.statsのnct(非心t分布)を使用
line_x = np.linspace(t.min(), t.max(), 1001)
ax.plot(line_x,
stats.nct.pdf(line_x, df=n-2, nc=rho / np.sqrt((1 - rho**2) / n)),
linewidth=2, color='tab:red')
# x軸ラベル、y軸ラベル、タイトルの設定
ax.set(xlabel='t', ylabel='Density', title=rf'$\rho$={rho}')
plt.tight_layout();【実行結果】
赤い線は自由度$${n-2}$$、非心度$$lambda}$$の非心t分布です。
母相関係数$${\rho}$$の3ケースともに、標本相関係数のヒストグラムの形状と非心t分布の確率密度関数の形状が(ほぼ)一致します。
■ 非心t分布の確率密度関数を描画する
非心度$${\lambda=0, 2, 5, 10}$$の4ケースで非心t分布の確率密度関数を可視化します。
### 173ページ 図4.27 さまざまな非心度の非心t分布
# 非心t分布のパラメータの設定
lambdas = [0, 2, 5, 10] # λ
nu = 23 # 自由度
# 描画用の設定
styles = ['-', '--', ':', '-.'] # 線種
line_x = np.linspace(-10, 20, 1001) # x軸の値
# 描画領域の設定
plt.figure(figsize=(8, 3))
# 4つのλごとに折れ線グラフの描画を繰り返し処理
for (lam, style) in zip(lambdas, styles):
# 折れ線グラフの描画
plt.plot(line_x, stats.nct.pdf(line_x, df=nu, nc=lam), ls=style,
label=f'$\lambda$={lam}')
# タイトル、x軸ラベル、y軸ラベル、凡例表示の設定
plt.title(f'非心t分布 (自由度ν={nu})')
plt.xlabel('t')
plt.ylabel('density')
plt.legend();【実行結果】
テキストの通り、非心度の値が大きくなるにつれて、右側にシフトしています。

非心t分布の「左右ずらし」の図も描画します。
### 173ページ 図4.28 非心度λの95%信頼区間の実現値
## 設定と準備
r = 0.5 # 標本相関係数の実現値
n = 25 # サンプルサイズ
nu = n - 2 # 非心t分布の自由度
t = (r * np.sqrt(nu) / np.sqrt(1 - r**2)) # Tの実現値
## λの上限・下限の探索
# 上限の探索
lambda_upper = t # 非心度の初期値
while True:
if (t < stats.nct.ppf(q=0.025, df=nu, nc=lambda_upper)):
break
# 非心度を1/1000ずつ大きくする
lambda_upper = lambda_upper + 1/1000
# 下限の探索
lambda_lower = t # 非心度の初期値
while True:
if (t > stats.nct.ppf(q=0.975, df=nu, nc=lambda_lower)):
break
# 非心度を1/1000ずつ小さくする
lambda_lower = lambda_lower - 1/1000
# λの下限・上限をnumpy配列化
lambda_vec = np.array([lambda_lower, lambda_upper])
## 描画処理
# 描画領域の設定
plt.figure(figsize=(10, 3.5))
# λの下限・上限ごとに描画を繰り返し処理
for i, lam in enumerate(lambda_vec):
# 描画領域の設定
ax = plt.subplot(1, 2, i+1)
# Tの実現値の算出
t = (r * np.sqrt(nu) / np.sqrt(1 - r**2))
# 非心t分布の確率密度関数の描画
x = np.linspace(-5, 10, 1001)
ax.plot(x, stats.nct.pdf(x, df=nu, nc=lam))
# 95%信頼区間の領域を塗りつぶし描画
lower = stats.nct.ppf(q=0.025, df=nu, nc=lam)
upper = stats.nct.ppf(q=0.975, df=nu, nc=lam)
x_fill = np.linspace(lower, upper, 1001)
ax.fill_between(x_fill, stats.nct.pdf(x_fill, df=nu, nc=lam), alpha=0.3)
# Tの実現値に実線を、非心度パラメータλに点線を描画
ax.axvline(t, color='tab:orange', label='Tの実現値')
ax.axvline(lam, ls='--', color='tab:red', label='$\lambda$')
# 塗りつぶし領域の端に線を描画
ax.hlines(0, x_fill.min(), x_fill.max(), lw=0.7)
ax.vlines(x_fill.min(), 0, stats.nct.pdf(x_fill.min(), df=nu, nc=lam), lw=0.7)
ax.vlines(x_fill.max(), 0, stats.nct.pdf(x_fill.max(), df=nu, nc=lam), lw=0.7)
# x軸ラベル、y軸ラベル、タイトルの設定
ax.set(xlabel='t', ylabel='density', title=f'非心t分布(自由度ν={nu})')
ax.legend();
plt.tight_layout();【実行結果】

■ 非心度$${\lambda}$$の信頼区間からはじめるシミュレーション
標本相関係数の実現値$${r=0.5}$$、サンプルサイズ$${n=25}$$、自由度 23 の条件で非心度$${\lambda}$$の95%信頼区間を探索型シミュレーションで見出します。
その後、非心度の95%信頼区間から「母相関係数の95%信頼区間」を求めます。
### 174ページ λの信頼区間の上限・下限に対応するρをシミュレーション
# 設定と準備
r = 0.5 # 標本相関係数の実現値
n = 25 # サンプルサイズ
nu = n - 2 # 非心t分布の自由度
t = (r * np.sqrt(nu) / np.sqrt(1 - r**2)) # Tの実現値
# 上限の探索
lambda_upper = t # 非心度の初期値
while True:
if (t < stats.nct.ppf(q=0.025, df=nu, nc=lambda_upper)):
break
# 非心度を1/1000ずつ大きくする
lambda_upper = lambda_upper + 1/1000
# 非心度λの信頼区間の上限
print(f'非心度λの信頼区間の上限 = {lambda_upper:.4f}')【実行結果】

対応する母相関係数の95%信頼区間の上限を算出します。
### 174ページ 続き
# 母相関係数ρの信頼区間の上限
print('母相関係数ρの信頼区間の上限 = '
f'{lambda_upper / np.sqrt(n + lambda_upper**2):.4f}')【実行結果】

続いて、非心度の95%信頼区間の下限と母相関係数の95%信頼区間の下限をシミュレーションします。
### 174ページ 続き
# 下限の探索
lambda_lower = t # 非心度の初期値
while True:
if (t > stats.nct.ppf(q=0.975, df=nu, nc=lambda_lower)):
break
# 非心度を1/1000ずつ小さくする
lambda_lower = lambda_lower - 1/1000
# 非心度λの信頼区間の下限
print(f'非心度λの信頼区間の下限 = {lambda_lower:.4f}')【実行結果】

### 175ページ 続き
# 母相関係数ρの信頼区間の下限
print('母相関係数ρの信頼区間の下限 = '
f'{lambda_lower / np.sqrt(n + lambda_lower**2):.4f}')【実行結果】

■ 回帰分析の仮定を満たすデータについて母相関係数の95%信頼区間をシミュレーション
テキストに従って、次の変数を乱数生成して、非心t分布を利用した母相関係数$${\rho}$$の95%信頼区間をシミュレーションします。
・変数$${X}$$:成功確率0.5 のベルヌーイ分布に従う確率変数
・変数$${Y}$$:平均$${2+0.5X}$$、分散$${1}$$の正規分布に従う確率変数
データのイメージをプロットします。
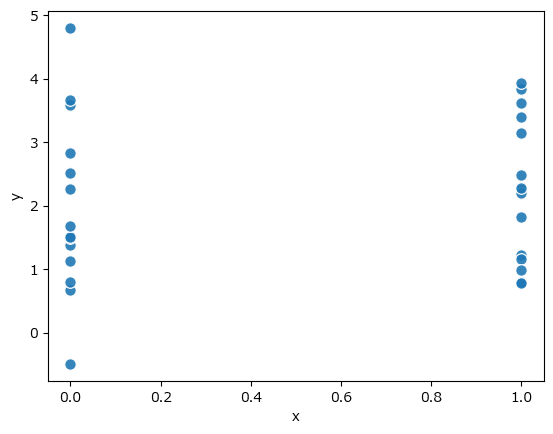
### 176ページ 図4.29 回帰分析の仮定を満たすサンプルデータ
## 設定と準備
n = 30 # サンプルサイズ
theta = 0.5 # ベルヌーイ分布の成功確率
a = 2 # 切片
b = 0.5 # 傾き
sigma_y = 1 # yにのせる正規分布ノイズの標準偏差
## x, yの値の設定
rng = np.random.default_rng(seed=1234)
x = rng.binomial(size=n, n=1, p=theta)
y = a + b*x + rng.normal(size=n, loc=0, scale=sigma_y)
## 描画
plt.scatter(x, y, s=70, ec='white', alpha=0.9)
plt.xlabel('x')
plt.ylabel('y');【実行結果】
シミュレーションします!
なお、R の MBESS パッケージに相当する Python のライブラリを見つけられなかったので、非心度$${\lambda}$$の信頼区間の下限・上限を探索する関数を定義します!
テキストオリジナルコードを改造して、処理時間短縮をはかりました。
### 非心t分布の非心度λの◯%信頼区間の下限・上限を算出する関数
# 引数 t:t値, nu:自由度, level:信頼区間の%。95%信頼区間のとき0.95
def confint_ncp(t, nu, level=0.95):
# 精度(10^-n乗)の上限値の設定
n_max = 5
# 信頼区間の下限% lower、上限% upperの算出
lower = (1 - level) / 2
upper = 1 - lower
## 非心度の下限の探索
# 10^-1, 10^-2, ・・・, 10^-n_maxへと精度を徐々に高くして非心度の下限を探索
for n in range(1, n_max + 1):
# 探索開始値の設定
if n == 1: # 非心度の初期値
lambda_lower = t
else: # forループ2回目以降は探索開始値を調整
lambda_lower = lambda_lower + 10**-(n-1)
# 精度nの水準で下限値を探索
while True:
# 非心度の%点がt値未満になったらwhileループを抜ける
if (t > stats.nct.ppf(q=upper, df=nu, nc=lambda_lower)):
break
# 非心度の下限探索値を1/10^nずつ小さくする
lambda_lower = lambda_lower - 10**(-n)
## 非心度の上限の探索
# 10^-1, 10^-2, ・・・, 10^-n_maxへと精度を徐々に高くして非心度の上限を探索
for n in range(1, n_max + 1):
# 探索開始値の設定
if n == 1: # 非心度の初期値
lambda_upper = t
else: # forループ2回目以降は探索開始値を調整
lambda_upper = lambda_upper - 10**-(n-1)
# 精度nの水準で上限値を探索
while True:
# 非心度の%点がt値超になったらwhileループを抜ける
if (t < stats.nct.ppf(q=lower, df=nu, nc=lambda_upper)):
break
# 非心度の上限探索値を1/10^nずつ大きくする
lambda_upper = lambda_upper + 10**(-n)
return lambda_lower, lambda_upperではシミュレーションの実行です!
2分ほど処理時間がかかります。
### 176ページ 回帰分布の仮定が満たされている場合に95%信頼区間が
# 母相関係数を95%の確率で含むことを確認するシミュレーション 約2分
## 設定と準備
n = 30 # サンプルサイズ
nu = n - 2 # 自由度
a = 2 # 変数Yを生成するための、切片
b = 0.5 # 変数Yを生成するための、単回帰係数
theta = 0.5 # 変数Xが従うベルヌーイ分布のパラメータ
sigma_x = np.sqrt(theta * (1 - theta)) # 変数Xの母標準偏差
sigma_y = 1 # 変数Yの母標準偏差
rho = b * sigma_x / sigma_y # 母相関係数
iter = 10000 # 標本を得る回数(標本数)
# 結果を格納するオブジェクト
true_num = 0 # 信頼区間内に母相関係数が含まれた回数
## シミュレーション
rng = np.random.default_rng(seed=5)
for i in range(iter):
# 変数xの生成: 0か1の二値変数
x = rng.binomial(size=n, n=1, p=theta)
# 変数yの生成
y = a + b*x + rng.normal(size=n, loc=0, scale=sigma_y)
# xとyの標本相関係数Rの実現値の算出
r = np.corrcoef(x, y)[0, 1]
# Tの実現値の算出
t = (r * np.sqrt(nu)) / np.sqrt(1 - r**2)
# 自作関数で非心度の95%信頼区間を推定
lambda_lower, lambda_upper = confint_ncp(t=t, nu=nu, level=0.95)
# 母相関係数の95%信頼区間の上限の算出
rho_upper = lambda_upper / np.sqrt(n + lambda_upper**2)
# 母相関係数の95%信頼区間の下限の算出
rho_lower = lambda_lower / np.sqrt(n + lambda_lower**2)
# 95%信頼区間内に母相関係数が含まれる場合、1カウントアップ
if (rho_lower <= rho) & (rho <= rho_upper):
true_num += 1
## 結果
true_num / iter【実行結果】
10000回のシミュレーションの結果、母相関係数が95%信頼区間に含まれた割合は約 95% となりました!
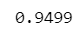

4.3.3 ブートストラップ法を用いた母相関係数の信頼区間
ブートストラップ法・・・
またまたパワーワードいただきました!
相関係数の推定は難解ですね~。
テキストはノンパラメトリック・ブートストラップ法を用います。
サンプルサイズ$${n}$$の標本の実現値から、$${n}$$個(サンプルサイズと同じ)の実現値を「無作為復元抽出」して得た標本をブートストラップ標本と呼びます。
テキストの言葉をお借りすると「あたかも標本の実現値を母集団化のようにみなす」のです!
ブートストラップ標本の数は延々増やせますね!
B個のブートストラップ標本それぞれから母数の推定量の実現値を算出して、この実現値の集合で母数を推定する方法がブートストラップ法です。

■ ノンパラメトリック・ブートストラップ法を用いた母相関係数の信頼区間のシミュレーション
1歩ずつ進めてまいります。
最初に標本データを作成します。
母相関係数$${\rho=0.5}$$、サンプルサイズ$${30}$$の2変量正規分布乱数です。
### 179ページ 2変量正規分布乱数を生成して相関係数を算出する関数
def boot_correlation(n, rho, seed=0): # empirical未対応
mu_vec = np.array([0, 5]) # 2変量の母平均ベクトル
sigma_vec = np.array([10, 20]) # 2変量の母標準偏差ベクトル
rho_matrix = np.array([[1, rho], [rho, 1]])
rng = np.random.default_rng(seed=seed)
dat_2norm = rng.multivariate_normal(
size=n, mean=mu_vec,
cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec),
)
# 2変量正規乱数
return {'data': dat_2norm, 'correlation': np.corrcoef(dat_2norm.T)[0, 1]}
rho = 0.5 # 母相関係数
n = 30 # サンプルサイズ
seed = 7 # 乱数シード
cor_nboot = boot_correlation(n=n, rho=rho, seed=seed)
cor_nboot['correlation']【実行結果】
標本データの標本相関係数は約 0.58 です。

この標本データを用いて、ノンパラメトリック・ブートストラップ法による母相関係数の 95% 信頼区間を算出します。
2000 個のブートストラップ標本を作成して、各ブートストラップ標本の標本相関係数を求めます。
### 180ページ ノンパラメトリック・ブートストラップ標本の標本相関係数を算出
## 設定と準備
dat_obs = cor_nboot['data']
B = 2000 # ブートストラップ標本数
# 結果を格納するオブジェクト
boot_r = np.zeros(B)
## シミュレーション
rng = np.random.default_rng(seed=123)
for i in range(B):
# 1, 2, ..., n(dat_obsの行数)の数列から、n個を復元抽出
row_num = rng.choice(a=len(dat_obs), size=len(dat_obs), replace=True)
# row_numに合致する行番号を抽出
resampled_data = dat_obs[row_num]
# ブートストラップ標本から、標本相関係数を求める
boot_r[i] = np.corrcoef(resampled_data.T)[0, 1]
print('ブートストラップ標本の相関係数(最初の5件):\n', boot_r[:5], '…')【実行結果】

2000個のブートストラップ標本の標本相関係数の外観を確認します。
まずはブートストラップ標本の標本相関係数の平均値から。
### 181ページ 続き
boot_r.mean()【実行結果】
標本データの標本相関係数 0.56 と近い値です。

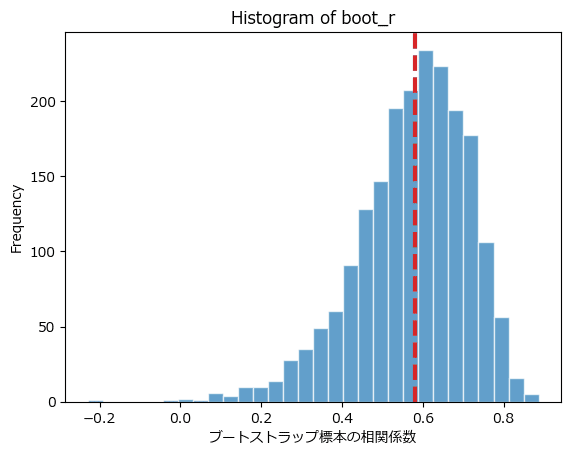
2000個の標本相関係数のヒストグラムを描画します。
### 181ページ 続き 図4.31 ブートストラップ標本から求めた標本相関係数のヒストグラム
## 結果
plt.hist(boot_r, bins=30, ec='white', alpha=0.7)
plt.axvline(cor_nboot['correlation'], lw=3, color='tab:red', ls='--')
plt.xlabel('ブートストラップ標本の相関係数')
plt.ylabel('Frequency')
plt.title('Histogram of boot_r');【実行結果】
いよいよ母相関係数の信頼区間の算出です。
最初に標本データを使用して、scipy.stat の pearsonr で 95% 信頼区間を算出します。
### 182ページ FisherのZ変換 母相関係数の信頼区間 scipy.statsのpearsonrを使用
result = stats.pearsonr(dat_obs[:, 0], dat_obs[:, 1])
print(result.confidence_interval(confidence_level=0.95))【実行結果】

続いてブートストラップ標本の相関係数の 2.5 パーセンタイルと 97.5 パーセンタイルに位置する相関係数を 95% 信頼区間の下限・上限とする方法です。
テキストは「ノンパラメトリック・ブートストラップ法によるパーセンタイル信頼区間」と呼んでいます。
numpy の quantile を利用します。
### 182ページ ノンパラメトリック・ブートストラップ法 numpyのquantile関数を使用
np.quantile(boot_r, q=[0.025, 0.975])【実行結果】
えっと、、、pearsonr の信頼区間と近くなってしまいました・・・
(テキストは pearsonr の信頼区間の方が区間が割と小さいです)
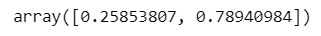
標本データのサンプルサイズを$${n=300}$$に拡大してシミュレーションします。
pearsonr の信頼区間とパーセンタイル信頼区間を算出します。
### 182ページ サンプルサイズn=300のシミュレーション
## n=300の乱数を作成
rho = 0.5 # 母相関係数
n = 300 # サンプルサイズ
seed = 123
cor_nboot = boot_correlation(n=n, rho=rho, seed=seed)
print('乱数の相関係数:', cor_nboot['correlation'])
## ブートストラップ標本の取得
# 設定と準備
dat_obs = cor_nboot['data']
B = 2000 # ブートストラップ標本数
# 結果を格納するオブジェクト
boot_r = np.zeros(B)
## シミュレーション
rng = np.random.default_rng(seed=123)
for i in range(B):
# 1, 2, ..., n(dat_obsの行数)の数列から、n個を復元抽出
row_num = rng.choice(a=len(dat_obs), size=len(dat_obs), replace=True)
# row_numに合致する行番号を抽出
resampled_data = dat_obs[row_num]
# ブートストラップ標本から、標本相関係数を求める
boot_r[i] = np.corrcoef(resampled_data.T)[0, 1]
print('ブートストラップ標本の相関係数(最初の5件):\n', boot_r[:5])【実行結果】

### 182ページ FisherのZ変換 scipy.statsのpearsonrを使用
result = stats.pearsonr(dat_obs[:, 0], dat_obs[:, 1])
print(result.confidence_interval(confidence_level=0.95))【実行結果】

### 182ページ ノンパラメトリック・ブートストラップ法
np.quantile(boot_r, q=[0.025, 0.975])【実行結果】

2つの信頼区間は区間幅が小さくなりました。

ブートストラップ標本数のシミュレーション
テキストはブートストラップ標本数$${B}$$が少ないときに注意が必要だとしています。
シミュレーションでさまざまなブートストラップ標本数の信頼区間を確認します。
母相関係数の信頼区間から離れて、ここでは母平均$${\mu}$$の信頼区間のシミュレーションで探ります。
最初に、標本データを作成します。
標準正規分布の$${n=50}$$の乱数を得て標本データとし、母平均の95%信頼区間を算出します。
### 182ページ 標準正規分布からn=50の乱数生成、母平均μ=0の95%信頼区間の実現値を算出
## 設定と準備
n = 50 # サンプルサイズ
rng = np.random.default_rng(seed=1) # 乱数生成器・乱数シード
rnd = rng.standard_normal(size=n) # 標準正規分布乱数の生成
## 1標本のt検定を実行してt統計量、p値、95%信頼区間を表示
result = stats.ttest_1samp(rnd, popmean=0)
print(result)
print(result.confidence_interval(confidence_level=0.95))【実行結果】
2行目が母平均の 95% 信頼区間です。
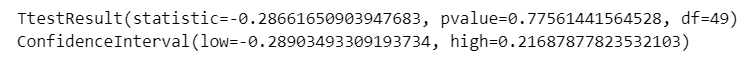
続いて、ノンパラメトリック法で母平均$${\mu}$$の パーセンタイル信頼区間を算出します。
ブートストラップ標本数$${B=10, 50, 100, 500, 1000, 1500, 2000}$$の7ケースでシミュレーションします。
### 183ページ ノンパラメトリック・ブートストラップ法のシミュレーション
## 設定と準備
# サンプルサイズnの標本の作成
n = 50
rng = np.random.default_rng(seed=1)
rnd = rng.standard_normal(size=n)
# 関数化 b:ブートストラップ標本の数
def boot_mean(B, seed=123):
rng = np.random.default_rng(seed=seed) # 乱数生成器・乱数シードの設定
boot_n = np.array([rng.choice(a=rnd, size=n, replace=True).mean()
for _ in range(B)])
return boot_n
# シミュレーションするブートストラップ標本の数をリスト化
B_vec = [10, 50, 100, 500, 1000, 1500, 2000]
# 結果を格納するオブジェクト
ci_upper = np.zeros(len(B_vec))
ci_lower = np.zeros(len(B_vec))
## シミュレーション
seed = 1
for i, B in enumerate(B_vec):
tmp = boot_mean(B, seed)
ci_lower[i], ci_upper[i] = np.quantile(tmp, q=[0.025, 0.975])
## 結果
data = pd.DataFrame(dict(num_B=B_vec, ci_lower=ci_lower, ci_upper=ci_upper))
display(data)【実行結果】
ブートストラップ標本数 num_B が大きくなるにつれて、信頼区間幅が小さくなり、$${B=1000}$$あたりで信頼区間の変化がほぼ無くなりました。

テキストはブートストラップ標本数が少ないときに乱数シードの影響を注意喚起しています。
乱数シードを変えて、同じシミュレーションを行ってみます。
### 185ページ 乱数シードを変えてシミュレーション
## 設定と準備
# 結果を格納するオブジェクト
ci_upper = np.zeros(len(B_vec))
ci_lower = np.zeros(len(B_vec))
## シミュレーション
seed = 10000
for i, B in enumerate(B_vec):
tmp = boot_mean(B, seed)
ci_lower[i], ci_upper[i] = np.quantile(tmp, q=[0.025, 0.975])
## 結果
data = pd.DataFrame(dict(num_B=B_vec, ci_lower=ci_lower, ci_upper=ci_upper))
display(data)【実行結果】
ブートストラップ標本数が少ない時、前のシミュレーション結果と全く異なる信頼区間になっています。

4.4 演習問題
4.4.1 演習問題1
標準偏差(標本分散の正の平方根)が母標準偏差の不偏推定量ではないことをシミュレーションで確かめます。
標準正規分布(母標準偏差$${\sigma=1}$$)に従う$${n=20}$$の標本の標本標準偏差を20000個取得して平均を取ります。
### 4.4.1 演習問題1
# 標本分散の正の平方根である標準偏差が母標準偏差の不偏推定量ではないことを
# シミュレーション
# 標準正規分布の例(母標準偏差はσ=1) 135ページのコードを参照
## 設定と準備
n = 20 # サンプルサイズ
iter = 20000 # 標本を得る回数(標本数)
## シミュレーション .std(ddof=0)で標本標準偏差を算出
rng = np.random.default_rng(seed=123)
sample_sd = np.array([rng.standard_normal(size=n).std(ddof=0)
for _ in range(iter)])
## 結果
sample_sd.mean()【実行結果】
シミュレーションで得た標本標準偏差の平方値 0.962 は母標準偏差 1 から乖離しており、標本分散の正の平方根が母標準偏差の不偏推定量では無いことが分かりました。

4.4.2 演習問題2
母平均の 95% 信頼区間シミュレーションについて、母集団分布を試行回数 5、成功確率 0.4 の二項分布で実践して、95% 信頼区間が母平均を含む割合を算出します。
### 4.4.2 演習問題2
# 4.2.3項の母平均の95%信頼区間シミュレーション
# 母集団分布をk=5, θ=0.4の二項分布に変更して実施 159ページのコードを参照
# Binomial(5, 0.4)の母平均は2=5*0.5
## 設定と準備
n = 20 # サンプルサイズ
k = 5 # 試行回数パラメータ
theta = 0.4 # 成功確率パラメータ
mu = k * theta # 母平均
iter = 100000 # 標本を得る回数(標本数)
## シミュレーション
rng = np.random.default_rng(seed=7)
# 100000個の標本平均(n=20)を取得
rnd = np.array([rng.binomial(size=n, n=k, p=theta) for _ in range(iter)])
# t統計量の算出
t = (rnd.mean(axis=1) - mu) / (rnd.std(ddof=1, axis=1) / np.sqrt(n))
# 95%信頼区間の実現値がt統計量を含む数をカウント
true_num_binom = ((stats.t.ppf(q=0.025, df=n - 1) <= t)
& (t <= stats.t.ppf(q=0.975, df=n - 1))).sum()
## 結果
# 母集団分布が二項分布のとき、95%信頼区間が母平均を含んだ割合
true_num_binom / iter【実行結果】
だいたい 95% になりました。

4.4.3 演習問題3
ノンパラメトリック・ブートストラップ法により、母平均のパーセンタイル信頼区間を求めます。
あわせて標本平均が正規分布に従う場合の 95% 信頼区間と比べます。
標本平均が正規分布に従う場合の 95% 信頼区間の算出には、scipy.stats の ttest_1samp() (1標本のt検定)を利用しました。
### 4.4.3 演習問題3
# ノンパラメトリック・ブートストラップ法により、母平均のパーセンタイル信頼区間を
# 算出、標本平均が正しく正規分布に従うときの95%信頼区間と比較する
# 母集団分布を標準正規分布と仮定 180ページおよび182ページのコードを参照
## 設定と準備
n = 50 # サンプルサイズ
rng = np.random.default_rng(seed=123)
dat_obs = rng.standard_normal(size=n) # 標準正規分布乱数
B = 2000 # ブートストラップ標本の数
# 結果を格納するオブジェクト
boot_mean = np.zeros(B)
## シミュレーション
rng = np.random.default_rng(seed=456)
for i in range(B):
# 1, 2, ..., n(dat_obsの行数)の数列から、n個を復元抽出
row_num = rng.choice(a=n, size=n, replace=True)
# row_numに合致する行番号のdat_obsを抽出
resampled_data = dat_obs[row_num]
# ブートストラップ標本から、平均をを求める
boot_mean[i] = resampled_data.mean()
## 結果:95%信頼区間
# パーセンタイル信頼区間
print('パーセンタイル信頼区間 ', np.quantile(boot_mean, q=[0.025, 0.975]))
# mu=X_bar, sigma=nbstd/sqrt(B)のt分布の95%信頼区間
result = stats.ttest_1samp(dat_obs, popmean=0)
print('正規分布に従うときの信頼区間',
result.confidence_interval(confidence_level=0.95)[:])【実行結果】
両者の 95% 信頼区間は近い結果になりました。

(おまけ)
標本平均が正規分布に従う場合の 95% 信頼区間の算出を scipy.stats の t.interval() (t分布の信頼区間)で算出するコードです。
stats.t.interval(loc=dat_obs.mean(), # 標本平均
scale=dat_obs.std(ddof=1) / np.sqrt(len(dat_obs)), # 標準誤差
confidence=0.95, df=len(dat_obs) - 1)【実行結果】

今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
