
10-2-4 重回帰モデルに対する分散分析 ~ CBT対応版の最後の問題です(最終話)
今回の統計トピック
分散分析の最後の問題です。
実は分散分析は、問題集CBT対応版の最終のテーマです。
ということで、この記事は最終話です。
重回帰モデルと一元配置分散分析表の結びつきを堪能しましょう。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
今回の記事の構成
この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」を1つの章にまとめます。
続く「実践する」で家賃データを用いた重回帰分析&分散分析を Python・EXCEL・R で実践いたします。
問題を解きながら知る
📘公式問題集のカテゴリ
線形モデルの分野 ~分散分析の分野
問4 重回帰モデルに対する分散分析(賃貸マンションの家賃)
試験実施年月
調査中
📕公式テキスト
・5.1.7 回帰の有意性の検定と回帰係数に関する検定(175ページ~)
・5.2.1 1元配置分散分析(185ページ~)
問題
公式問題集をご参照ください。
解き方
題意
重回帰モデルに関して、問題文に記載された「統計ソフトウェアの出力結果」と「一元配置分散分析表(穴開き)」に基づいて、次の2問を解答します。
問1.一元配置分散分析表の穴埋め
問2.回帰の有意性の検定
【条件】
・次の重回帰モデルを取り扱う
$${家賃=\alpha_0+\alpha_1\times 部屋の大きさ +\alpha_2 \times 築年数 + u}$$
・誤差項$${u}$$は互いに独立に平均$${0}$$、分散$${\sigma^2_u}$$の正規分布に従う
・回帰係数を最小二乗法で推定
問1:一元配置分散分析表の穴埋め
問題文で既に計算済みですが、統計ソフトウェアの出力結果と一元配置分散分析表の繋がりを改めて確認します。

残差の標準誤差$${9.904}$$、自由度$${185}$$、残差の標準誤差の数式から、残差平方和を求められます。
決定係数$${0.8512}$$、残差平方和、決定係数の数式から、総平方和を求められます。
平方和・自由度によって、統計ソフトウェアの出力結果と一元配置分散分析表が繋がっています!
では、一元配置分散分析表の穴埋めに進みます!
回帰モデルの一元配置分散分析表の計算メカニズムは次のようになります。
$$
\begin{array}{|c|c:c:c:c|}
\hline
変動要因 & 平方和 & 自由度 & 平均平方 & F \\
\hline
回帰 & S_R & p & V_R = S_R / p & F = V_R / V_e \\
\hdashline
残差 & S_e & n-p-1 & V_e = S_e / (n-p-1) & - \\
\hline
合計 & S_T & n-1 & - & - \\
\hline
\end{array}
$$
回帰による平方和の自由度は、説明変数の数$${p}$$です。
重回帰モデルの説明変数は「部屋の大きさ」と「築年数」の2つです。
よって、回帰による平方和の自由度は$${2}$$です。
ここまでで分かったことを一元配置分散分析表に記入しましょう。
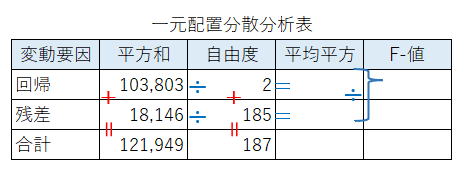
「平均平方」と「F-値」は青字の割り算を行って算出します。
$${回帰の平均平方=103803/2 \fallingdotseq 51902}$$
$${残差の平均平方=18146/185 \fallingdotseq 98}$$
$${F値=51902/98 \fallingdotseq 529}$$
全て計算できました。
一元配置分散分析表を完成させましょう。

解答選択肢(ア)回帰の自由度は$${2}$$、(オ)F-値は$${529}$$です。
問1の解答は ③ です。

問2.回帰の有意性の検定
一元配置分散分析表を用いて、有意水準$${5\%}$$で回帰の有意性の検定を行います。
・帰無仮説$${H_0}$$:回帰は有意ではない
・対立仮説$${H_1}$$:回帰は有意である
一元配置分散分析表の$${F}$$値は自由度$${(p, n-p-1)}$$の$${F}$$分布に従います。
重回帰モデルの分散分析表の公式を確認しましょう。
$$
\begin{array}{|c|c:c:c:c|}
\hline
変動要因 & 平方和 & 自由度 & 平均平方 & F \\
\hline
回帰 & S_R & p & V_R = S_R / p & F = V_R / V_e \\
\hdashline
残差 & S_e & n-p-1 & V_e = S_e / (n-p-1) & - \\
\hline
合計 & S_T & n-1 & - & - \\
\hline
\end{array}
$$
$${F}$$値の分子は回帰の平均平方、分母は残差の平均平方です。
自由度に関しては、分子側の$${p}$$が第1自由度、分母側の$${n-p-1}$$が第2自由度です。
あわせて$${F}$$検定統計量の公式を確認しましょう。
$$
F=\cfrac{V_R}{V_e}=\cfrac{S_R/p}{S_e/(n-p-1)}=\cfrac{(S_R/\sigma^2)/p}{(S_e/\sigma^2)/(n-p-1)} \sim F(p, n-p-1)
$$
$${F}$$検定統計量は自由度$${(p, n-p-1)}$$の$${F}$$分布に従います。
第1自由度は$${p}$$、第2自由度は$${n-p-1}$$です。
本問題に当てはめると、第1自由度である回帰の自由度は$${2}$$、第2自由度である残差の自由度は$${185}$$です。

解答選択肢の中で、自由度$${(2, 185)}$$を含んでいるのは ③ のみです。
問2の解答は ③ です。

「回帰の有意性の検定」の続き
回帰の有意性の検定を続けましょう。
$${F}$$分布のパーセント点表より、自由度$${(2,185)}$$の上側$${5\%}$$点を取得しましょう。
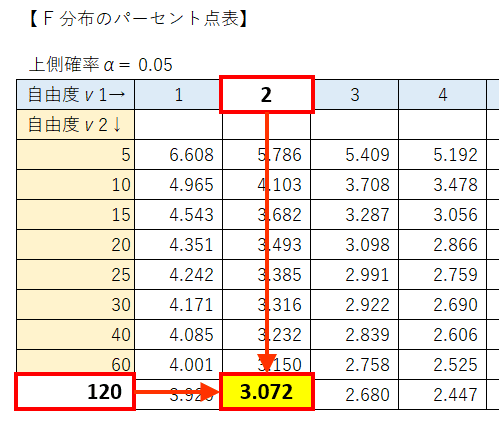
第2自由度の最大値は$${120}$$です。
他の欄を見ると、第2自由度の値が大きくなるほど、上側$${5\%}$$点の値は小さくなります。
つまり、第2自由度が$${185}$$の上側$${5\%}$$点は、$${120}$$の上側$${5\%}$$点よりも小さいのです。
上側$${5\%}$$点が大きければ、棄却域は小さくなり、帰無仮説は棄却されにくくなります。
検定のハードルが高くなるのです。
ここではハードルの高い第2自由度$${120}$$の上側$${5\%}$$点$${3.072}$$を利用しましょう。
$${F}$$値は$${529}$$であり、上側$${5\%}$$点である$${3.072}$$よりも大きいです。
つまり、有意水準$${5\%}$$で帰無仮説は棄却されます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、対立仮説「回帰は有意である」と言えます。
「回帰が有意である」は、「回帰モデルの回帰係数のどれかはゼロではない」「目的変数に影響を与える説明変数がある」という意味になります。
自由度$${(2,185)}$$の$${F}$$分布のグラフに、$${F}$$値と上側$${5\%}$$点を描画して、$${F}$$値が棄却域に含まれていることを確かめましょう。
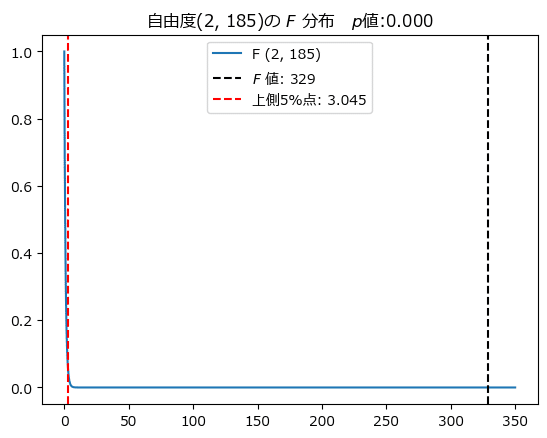
黒い点線の$${F}$$値は、赤い点線の上側$${5\%}$$点よりも上側の棄却域に含まれています!
$${p}$$値は0.000、上側$${5\%}$$点は$${3.045}$$です。
一元配置分散分析表の最終化
一元配置分散分析表を最終化しましょう。

「回帰係数の有意性の検定」
少々視点を変えて、「回帰係数の有意性の検定」を考えます。
重回帰モデルの回帰係数の値は次のとおりです。
・変数「大きさ」の回帰係数:$${2.83278}$$
・変数「築年数」の回帰係数:$${-1.18052}$$
・切片(Intercept):$${33.42282}$$
これらの回帰係数1つ1つが「ゼロではない=目的変数に影響を与える」かどうかの検定が、回帰係数の有意性の検定です。
問題で明かされている統計ソフトウェアの出力結果に回帰係数の有意性に関する情報が含まれています。

赤枠部分は、回帰係数の有意性に関する$${t}$$検定の$${p}$$値です。
有意水準を$${5\%}$$としましょう。
切片(Intercept)、大きさの傾き、築年数の傾きのすべての$${p}$$値は、極小値($${2 \times 10^{-16}}$$)であり、有意水準$${5\%}$$より小さいです。
【結論】
有意水準$${\boldsymbol{5\%}}$$ですべての回帰係数は有意であり、「どの回帰係数もゼロではない」「すべての回帰係数は目的変数に影響を与えている」と言えます。
統計ソフトウェアの出力結果と一元配置分散分析表の両方を堪能いたしました。
解答
〔1〕③、〔2〕③ です。
難易度 やさしい
・知識:重回帰モデルの一元配置分散分析表
・計算力:数式組み立て(低)、電卓(低)
・時間目安:2問合計 3分
実践する
線形重回帰分析と一元配置分散分析を実践する
家賃データを用いて線形重回帰分析と一元配置分散分析を実践します。
Python、EXCEL、R の3ツールで実践します!
家賃データの取得
リアリティを感じられるデータ分析をしたいと考えて、ネットで家賃データを探したところ、「TOKYOリスタイル」様のWebサイトで、東京のある地域のサンプルデータを見つけました。
記事主様は、家賃データの重回帰分析をEXCELで行っています。
記事を拝読して、データ分析の大切さを改めて噛み締めました!
【謝辞】
「TOKYOリスタイル」様、「三軒茶屋駅」周辺の家賃データをお借りいたします。
ありがとうございます!
Webサイトの「サンプルデータをダウンロード」にて、サンプルデータ(EXCELファイル)をダウンロードします。

ファイル名は「reference_sample.xlsx」(初期表示値)とし、Python の Jupyter Notebook ファイルと同じフォルダに保存します。


Pythonで作成してみよう!
Python を道具にして、重回帰分析と分散分析を実施します。
プログラムはどうも・・・という方は、ぜひ、実行結果の表やグラフをご堪能ください。
① インポート
いろんなライブラリを利用します。
### インポート
# 数値計算
import pandas as pd
import numpy as np
from itertools import combinations
# 統計処理
from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
import pingouin
import lmdiag
# 評価指標
from sklearn.metrics import mean_squared_error, mean_absolute_error
# 可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'② データの読み込みと前処理
ダウンロードしたEXCELファイルを pandas のデータフレームに読み込みます。
「三軒茶屋駅」周辺物件の分析を行うので、シート名は「三茶結果」を指定します。
### データの読み込み
# 列名の設定
# 物件名:name, 家賃:rent, 面積:area, 駅からの徒歩分:walk, 築年月:built_date
col_names = ['name', 'rent', 'area', 'walk', 'built_date']
# EXCELの読み込み
df = pd.read_excel('reference_sample.xlsx', # EXCELファイル名
sheet_name='三茶結果', # EXCELシート名
skiprows=[0, 1], # 読み飛ばす行
names=col_names) # 列名
# データの表示
print('df.shape: ', df.shape)
display(df.head())
print(df.info())【実行結果】

580の物件データです。
変数は次の5つです。
なお、全ての変数に欠損値は無いです(580 non-null)。
・name:物件名(実際の名称ではないです)
・rent:家賃(円)-整数型
・area:面積(㎡)-浮動小数点型
・walk:駅からの徒歩時間(分)-整数型
・built_date:築年月-日付型
データを加工します。
築年月を築月数(建築後、何ヶ月経過しているか)に変更します。
築月数算出の基準年月は「2022年11月」に仮設定します。
「TOKYOリスタイル」様記事の更新年月に合わせました。
まず、築月数を算出する関数を定義します。
### 築年月を築月数に変換する関数の定義
# pandas.Seriesの日付機能を活用する
def calc_months(x, base_date):
# 基準日(引かれる数)の加工:引数base_dateを文字列から日付型に変換してSeries化
minuend_date = pd.Series(pd.to_datetime(base_date))
# 築日付(引く数)の加工:引数xをSeries化
subtrahend_date = pd.Series(x)
# 戻り値:築月数
# 築月数=「築日付-基準日」の月数 ※dt.yaerで年、dt.monthで月を取得
return (minuend_date.dt.year - subtrahend_date.dt.year) * 12 \
+ (minuend_date.dt.month - subtrahend_date.dt.month)続いて、築月数に変換する処理を実行します。
### 築月数:ageの作成
# データフレームのコピー
data = df.copy()
# 築月数の作成:applyメソッドでcalc_monthsを適用。引数に基準日2022年11月1日を設定
data['age'] = data['built_date'].apply(calc_months, args=('2022-11-01',))
# 築年月built_dateを削除
data = data.drop('built_date', axis=1)
# 先頭5行を表示
display(data.head())
# 加工後のデータフレームをファイルに保存
# data.to_csv('sampledata.csv', index=False, encoding='utf_8_sig')【実行結果】

築月数(age)が追加され、築年月(built_date)を削除しました。
最後に目的変数と説明変数をリストに格納します。
家賃を予測する重回帰分析を行うので、目的変数は家賃 rent です。
### カラム名の取得
# 目的変数
target_col = 'rent'
# 説明変数
feature_cols = data.columns[2:].to_list()
print('feature_cols: ', feature_cols)【実行結果】

説明変数のリスト feature_cols に area, walk, age の3変数の名称を格納しました。
■ 加工済みの CSV ファイルを利用する場合
こちらのリンクから「家賃データ」の CSV ファイルをダウンロードして、次のコードでデータの読み込みを行ってください。
この CSV ファイルは age(築月数)に変換済みです。
### csvファイルの読み込み
data = pd.read_csv('./sampledata.csv')
### カラム名の取得
# 目的変数
target_col = 'rent'
# 説明変数
feature_cols = data.columns[2:].to_list()
print('feature_cols: ', feature_cols)③ データの概要の確認
ひとまず、pandas の describe を実行して要約統計量を確認します。
### 要約統計量の表示
data.describe()【実行結果】

家賃は 37,000円~146,000円(中央値は80,000円)、築月数は 37 か月(約3年)~ 740 か月(60年超)まで様々です。
続いて説明変数のヒストグラムと各変数間の散布図を確認します。
seaborn の pairplot を利用して、一度に描画します。
### ヒストグラムと散布図の描画:seabornのpairplotの利用
sns.pairplot(
data[feature_cols + [target_col]], # 描画するデータ
kind='reg', # 回帰直線付き散布図regplotを指定
corner=True, # 行列右上を非表示
diag_kws={ # 対角要素の引数
'ec': 'white'}, # ヒストグラムの輪郭線の色
plot_kws={ # 非対角要素の引数
'ci': None, # 回帰直線の信頼区間を非表示
'scatter_kws': { # 散布図の引数
's': 10, # 散布図の点のサイズ
'alpha': 0.5}, # 散布図の点の透明度
'line_kws': { # 回帰直線の引数
'color': 'red'}, # 回帰直線の色
},
);【実行結果】
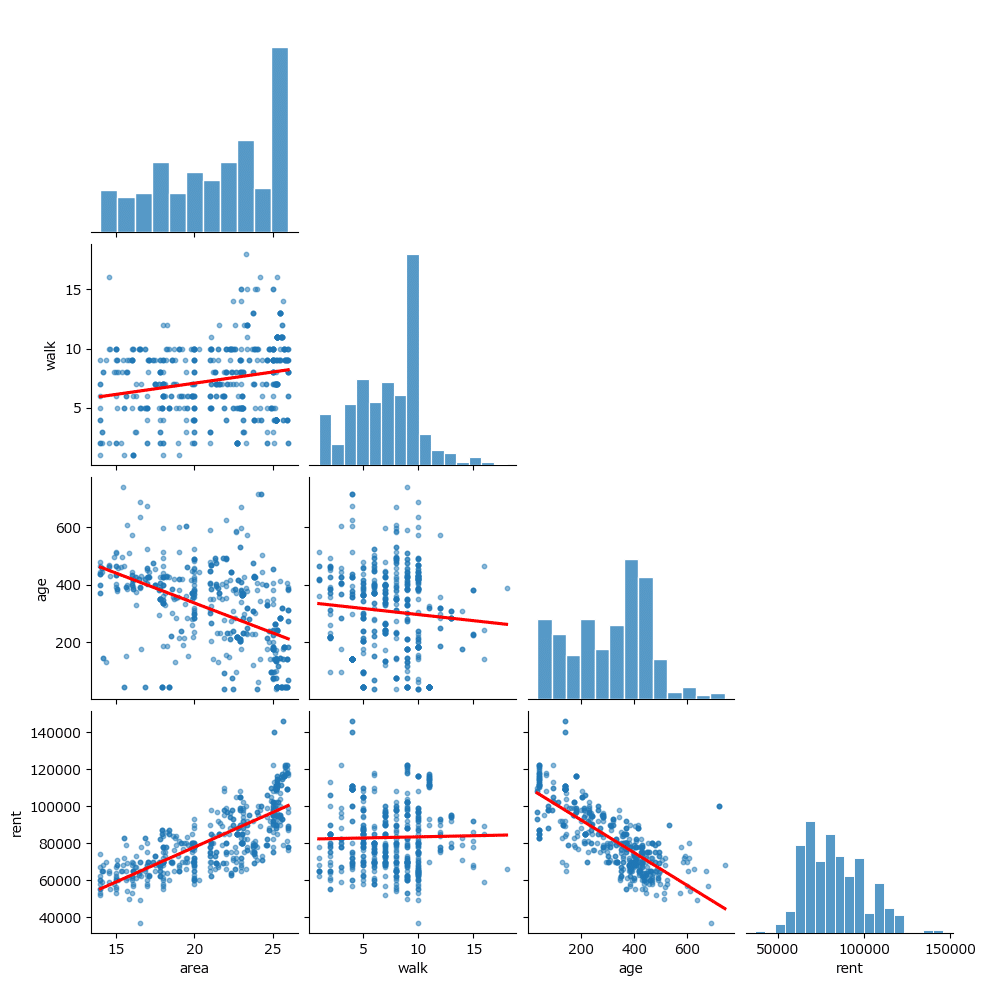
【ヒストグラムの所感】
・面積は25㎡以上が多いようです。
もしかすると26㎡以上は「26」にまとまっているのかもしれません。
・家賃はベル型に見えますが、15万円が飛び地のように外れて存在します。
【説明変数と目的変数の関係の所感】
一番下の行に説明変数と目的変数の散布図があります。
面積は正の相関、築月数は負の相関がありそうです。
徒歩(分)と家賃の相関は無さそうな感じです。
【説明変数間の関係の所感】
・面積と築月数に弱めの負の相関がありそうです。
築浅の方が面積が広いのでしょうか・・・。
相関係数を確認しましょう。
### 相関行列の表示
# corr関数で相関行列を取得
corr = data.corr(numeric_only=True)
# 相関行列の表示
display(corr)
# 相関行列をヒートマップで可視化
sns.heatmap(data=corr, annot=True);【実行結果】


散布図で確認したことが数値で明確になりました。
walk(徒歩分)とrent(家賃)の相関がほぼ無いです。
データの徒歩分は 1~18 分です。
三軒茶屋駅から徒歩 18分 程度なら家賃には影響しないのでしょうか・・・。
偏相関係数を確認しましょう。
偏相関係数では、他の変数の影響を取り除いて相関を見ることができます。
偏相関係数の算出には pingouin の pcorr() を利用します。
### 偏相関係数の表示
data.iloc[:, 1:].pcorr().round(3)【実行結果】
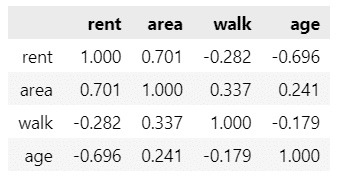
walk(徒歩分)とrent(家賃)の偏相関係数は -0.282 です。
最寄り駅から離れるほど家賃が安くなるという、弱い負の相関関係が明らかになりました。
肌感覚に合った相関関係を確認できました!
3つの説明変数は目的変数:家賃に影響していそうな予感がします。
④ 回帰分析
3つの説明変数の全てを使うのがよいか、少ない説明変数に限定するのが良いのか、モデルの評価指標を見ながら考えましょう。
説明変数の全ての組み合わせで線形回帰モデルを作って、評価指標を取得しましょう。
少々長めのコードです。
「sm.OLS(data[target_col], sm.add_constant(data[features])).fit()」で線形回帰モデルを設定しています。
### 説明変数の組み合わせごとに回帰分析を実施して評価指標を取得
## 説明変数の組み合わせをリスト化
# ・for文を回して組み合わせに入れる説明変数の数(1~3)を指定
# ・itertoolsのcombinationsで説明変数の数(1~3)ごとの組み合わせを取得
feat_combi_list = []
for num in range(len(feature_cols)):
for combi in combinations(feature_cols, num+1):
feat_combi_list.append(list(combi))
print('説明変数の組み合わせ:\n', feat_combi_list)
## 回帰分析の実施
# ・説明変数の組み合わせごとにstatsmodelsのOLS(線形回帰分析)を実行
# ・分析結果から自由度調整済み決定係数、RMSE、MAE, AIC, BICを算出してリスト化
adj_R2, rmse, mae, aic, bic = [], [], [], [], []
for features in feat_combi_list:
# 回帰分析の実行
results = sm.OLS(data[target_col], sm.add_constant(data[features])).fit()
# モデルの自由度調整済み決定係数、RMSE、MAE、AIC、BICをリスト化
adj_R2.append(results.rsquared_adj)
rmse.append(mean_squared_error(data[target_col], results.fittedvalues,
squared=False))
mae.append(mean_absolute_error(data[target_col], results.fittedvalues))
aic.append(results.aic)
bic.append(results.bic)
## 評価指標をデータフレーム化
result_df = pd.DataFrame({
'説明変数': feat_combi_list,
'Adj_R2' : adj_R2,
'RMSE': rmse,
'MAE': mae,
'AIC': aic,
'BIC': bic,
})
## 自由度調整済み決定係数で降順ソートして評価指標を表示
display(result_df.sort_values(by='Adj_R2', ascending=False).round(3))【実行結果】
次の7通りの組み合わせで線形回帰モデルを設定しました。


自由度調整済み決定係数 Adj_R2の大きな順に並べました。
【各指標の概要】
◆自由度調整済み決定係数 Adj_R2
値が大きいほど、当てはまりの良いモデル
◆RMSE、MAE
目的変数の観測値(実際のデータ)と予測値の誤差の大きさを示す指標
値が小さい方が誤差の小さいモデル
◆AIC、BIC
モデルの当てはまりの良さとモデルの簡潔さのバランスをとる選択の指標
値が小さいほど、よいモデルと評価
全ての評価指標で、3つの説明変数を用いたモデルが1番よい結果となりました。
以降は、3つの説明変数を用いる重回帰モデルを検討します。
⑤ 重回帰モデルの分析
statsmodels の formula api (Rライクなapi)で回帰分析を実施します。
formula を 'rent ~ area + walk + age' と指定することで、3つの説明変数を回帰モデルに設定しています。
### 3つの説明変数を用いた回帰分析の実行
results = smf.ols('rent ~ area + walk + age', data=data).fit()
# 回帰式の表示
print(f'回帰式: rent = {results.params.Intercept:.3f} '
f'{results.params.area:+.3f}*area {results.params.walk:+.3f}*walk '
f'{results.params.age:+.3f}*age\n')
# 回帰分析の結果の表示
print(results.summary())【実行結果】
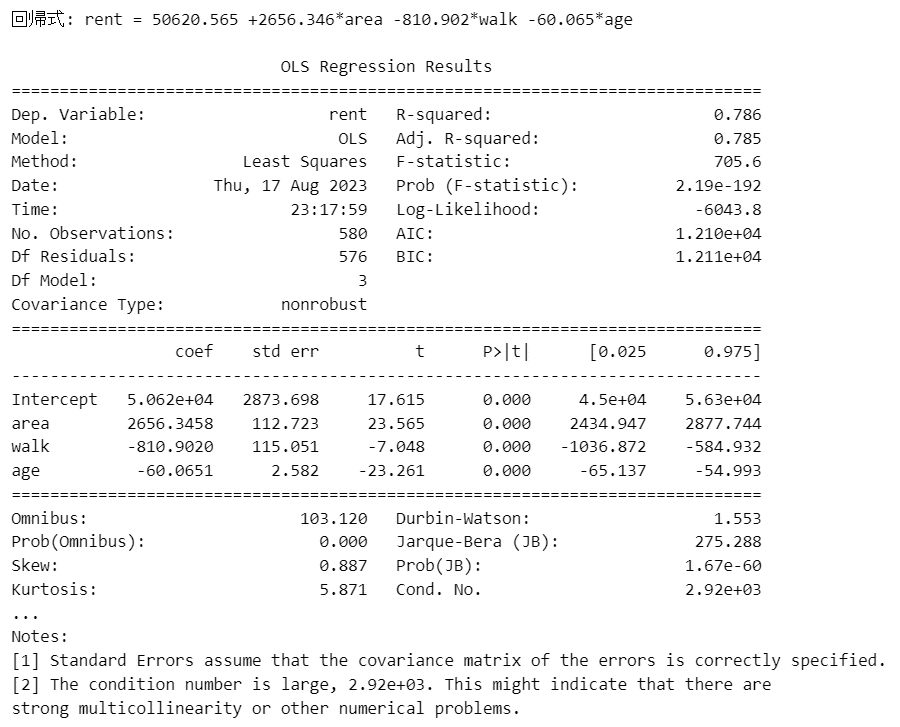
【回帰式】
$${家賃=50620.565+2656.346 \times 面積㎡ -810.902 \times 徒歩分 -60.065 \times 築月数}$$
・面積が1㎡増えると家賃は2656円増加します。
・駅からの徒歩が1分増えると家賃は810円減少します。
・築月数が1か月増えると家賃は60円減少します。
【回帰の有意性の検定】
$${F}$$値の$${p}$$値(Prob(F-statistic))は$${0.000 \cdots}$$です。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.000 \cdots}$$は有意水準より小さいので、帰無仮説を棄却できます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、この回帰モデルは有意である(偏回帰係数のどれかは目的変数に影響を与える)と言えます。
【回帰係数の有意性の検定】
各回帰係数の$${t}$$値の$${p}$$値(P > | t |)は$${0.000 \cdots}$$です。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.000 \cdots}$$は有意水準より小さいので、帰無仮説を棄却できます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、すべての偏回帰係数は有意である(全ての回帰係数は目的変数に影響を与える)と言えます。
⑥ 分散分析の実行
statsmodels の anova_lm で一元配置分散分析を実行します。
### 分散分析の実行
# データフレームの表示桁数の設定
pd.options.display.float_format = '{:,.2f}'.format
# 一元配置分散分析の実行 statsmodelsのanova_lmを利用
anova = sm.stats.anova_lm(results, typ=1)
display(anova)【実行結果】

回帰の行は偏回帰係数に分かれて表示されます。
回帰の行、合計の行を付け足してみましょう。
### 「回帰」と「合計」の行を追加した一元配置分散分析表の表示
## 回帰行の編集
# 回帰の自由度の算出
reg_df = anova.loc[['area', 'walk', 'age'], 'df'].sum()
# 回帰のSeriesを作成 :自由度、平方和、平均平方、F値、p値
regs = pd.Series([reg_df, results.ess, results.mse_model, results.fvalue,
results.f_pvalue],
index=anova.columns, name='Regression')
## 合計行の編集
# 合計の自由度と平方和の算出
total_df = anova.loc['Residual', 'df'] + reg_df
total_sum_sq = results.ess + results.ssr
# 合計のSeriesを作成 :自由度、平方和、その他の項目は欠損値
totals = pd.Series([total_df, total_sum_sq, np.nan, np.nan, np.nan],
index=anova.columns, name='Total')
## データフレームを統合 1列のみのデータはto_frame().Tで縦のデータフレーム化
anova = pd.concat([anova.iloc[:3, :], # area~ageの行
regs.to_frame().T, # Regressionの行
anova.iloc[3, :].to_frame().T, # Residualの行
totals.to_frame().T], # Totalの行
axis=0)
## 一元配置分散分析表の表示
display(anova)【実行結果】

できました!
下の3行が2級テキストに記載される重回帰モデルの一元配置分散分析表に相当します。
⑦ 残差診断プロットの確認
statsmodels の出力結果で、下図の赤枠の確率は、残差の正規性の仮定(残差が正規分布に従う仮定)に関する検定に用います。
両方の確率が$${0.000 \cdots}$$であるので、残差が正規分布に従っていないことを示唆しています。

残差診断プロットを確認しましょう。
あわせて、残差の独立性、残差の等分散性、外れ値を確認しましょう。
lmdiag ライブラリを利用します。
必要に応じてインストールしましょう。
### 残差診断プロットの描画
# pip install lmdiag
plt.figure(figsize=(12, 12))
lmdiag.plot(results);【実行結果】

◆残差の独立性、等分散性◆
左の2つのグラフを見ると、残差の各点がバラバラにプロットされていて、傾向などが見られないです。
おそらく、残差の独立性と等分散性は問題無さそうです。
◆残差の正規性◆
右上の正規Q-Qプロットを見ましょう。
残差の各点が赤い点線にのっていると正規性ありと判断できます。
右上の各点が赤い点線から大きく乖離しているので、正規性の仮定は満たされていない可能性が高いです。
◆外れ値◆
右下のグラフを見ましょう。
外れ値がある場合、外れ値の残差の点が赤い点線よりも外側に現れます。
このグラフには赤い点線が表示されていないので、外れ値は無いと想定できます。
■ 残差の正規性の仮定が満たされない場合の影響
$${F}$$値を用いた回帰の有意性の検定の判定が不正確になる可能性があります。
$${F}$$検定統計量が$${F}$$分布に従うと仮定できる条件の1つが、残差が正規分布に従うことだからです。
■ まとめ
【統計的な観点】
統計的な文脈では、この線形重回帰モデルは見直しするほうがよい、という意見が出るでしょう。
変数を変換する、交互作用項を加えるなどの別のモデルを検討する、といった解決策があるようです。
実は、対数変換、Box-Cox変換などで変数を変換してモデル構築を試みたのですが、残差の正規性を確保できませんでした。
また、交互作用項は統計検定2級の試験範囲から(おそらく)外れるので、ここでの深掘りはやめようと思います。
【機械学習の観点】
機械学習などの文脈では、予測精度の高さや説明のしやすさの観点でモデルを評価する模様です。
線形回帰モデルは説明のしやすさは確保できているので、残りのテストデータによる予測精度評価に基づいて、今回の重回帰モデルを利用するかどうかの判断がなされると思われます。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

EXCELで作成してみよう!
データ分析機能の「回帰分析」を利用して、さまざまな説明変数の組み合わせで回帰分析を実施してみましょう。
データの概要
「データ」シートに家賃データを格納しています。
age(築月数)に変換済みです。

回帰分析の手順
メニューより、「データ」>「データ分析」を指定して、「データ分析」画面を開き、「回帰分析」を指定して「OK」ボタンをクリックします。

「回帰分析」画面の入力範囲に項目名を含めたデータの範囲を指定します。(赤枠、青枠の対応関係です)
「ラベル」と「残差」にチェックを入れましょう。
新規ワークシートを選択して、回帰分析シートを作成します。
「OK」ボタンをクリックすると、回帰分析の結果が表示されます。

回帰分析の結果の確認
全7パターンの回帰分析はこちらです!
① 説明変数:area, walk, age

② 説明変数:area, walk

③ 説明変数:walk, age

④ 説明変数:area, age

⑤ 説明変数:area

⑥ 説明変数:walk

⑦ 説明変数:age

■ まとめ表
7つの回帰モデルの評価指標を1表にまとめました。
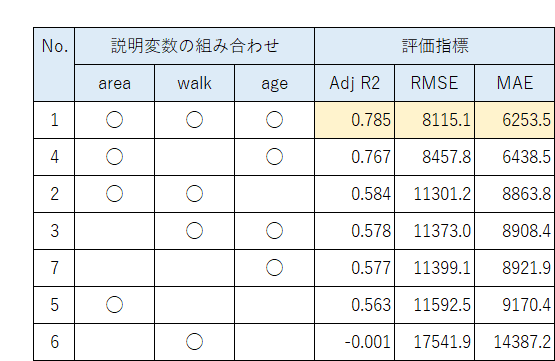
すでにPythonの結果で分かっているかもですが・・・。
3つの説明変数をすべて用いたモデルの評価指標が、すべて1番よい結果となりました。
ベストモデルの偏回帰係数を確認しましょう。

【回帰式】
$${家賃=50620.56+2656.35 \times 面積㎡ -810.90 \times 徒歩分 -60.07 \times 築月数}$$
■ 回帰係数の有意性の検定
各回帰係数の$${t}$$値の$${p}$$値(P-値)は$${0.000 \cdots}$$です。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.000 \cdots}$$は有意水準より小さいので、帰無仮説を棄却できます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、すべての偏回帰係数は有意である(全ての回帰係数は目的変数に影響を与える)と言えます。
■ 一元配置分散分析表

■ 回帰の有意性の検定
$${F}$$値の$${p}$$値(有意F)は$${0.000 \cdots}$$です。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.000 \cdots}$$は有意水準より小さいので、帰無仮説を棄却できます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、この回帰モデルは有意である(偏回帰係数のどれかは目的変数に影響を与える)と言えます。
■ RMSE、MAE の計算方法
回帰分析の結果から RMSE と MAE を簡単に計算できます。
① RMSE(二乗平均平方根誤差)

青い色の「残差の変動」は残差平方和です。
RMSEは、残差平方和をデータ数で割り(これがMSE:平均二乗誤差)、平方根をとった値です。
緑の枠で「残差の変動」÷「観測数」の平方根を計算しています。
② MAE(平均絶対誤差)

MAE は残差の絶対値の合計をデータ数で割った値です。
残差は回帰分析表の下部にあります。青い部分です。
絶対値は EXCEL の ABS 関数で計算します。
緑の枠で「残差」の絶対値を合計して「観測数」で割っています。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

R で作成してみよう!
R スクリプトで回帰分析を実践します。
コードはめっちゃシンプルです。
CSVファイルのダウンロード
こちらのリンクから「家賃データ」のCSVファイルをダウンロードできます。
age(築月数)に変換済みです。
① データの読み込み
age(築月数)に変換済みの CSV ファイルを読み込みます。
### データの読み込み
data <- read.csv("sampledata.csv")
# データの要約表示
str(data)
summary(data)【実行結果】
データの項目の概要と要約統計量を表示しました。

② 相関係数の表示
相関行列を表示します。
### 相関係数の計算
cor(data[2:5])【実行結果】
1行目に目的変数 rent(家賃)と3つの説明変数の相関係数を表示しています。
rent(家賃)は area(面積)と age(築月数)と強めの相関があります。

セ・パ両リーグの基本統計量が表示されました。
データの数(n)、平均(mean)、標準平均(sd)、中央値(median)、最小値(min)、最大値(max)などを確認できます。
平均値の差は、$${233.67-185.33=48.34}$$(万人)です。
③ 相関行列の描画
corrplot を用いて相関係数の大きさを可視化しましょう。
### 相関行列の描画 by corrplot
# install.packages("corrplot")
library(corrplot)
corrplot(cor(data[2:5]))【実行結果】
円の大きさで相関の強さを、円の色で相関の正・負を示しています。
area(面積)とage(築月数)の間に少し相関関係がありそうです。

④ 散布図行列の描画
psych を用いて散布図を描き、変数間の関係を可視化しましょう。
### 散布図行列の描画 by psych
# install.packages("psych")
library(psych)
psych::pairs.panels(data[, seq(2, 5)])【実行結果】
左端の rent(家賃)の列を見ましょう。
area(面積)と age(築月数)は rent(家賃)との間に相関関係があることが、よくわかります。
また、各変数のヒストグラムでは area(面積)の分布が広い側に、walk(徒歩分)が駅近に、age(築月数)が築浅に偏っていることが分かります。

⑤ 回帰分析の実行
真打ちの登場です。
「lm(rent ~ area + walk + age, data=data)」の部分は、Python の statsmodels の formula api とほぼ同じ構文です。
### 回帰分析の実施と結果表示
data.lm <- lm(rent ~ area + walk + age, data=data)
summary(data.lm)【実行結果】
統計検定の出題でおなじみの「統計ソフトウェアの出力結果」です!
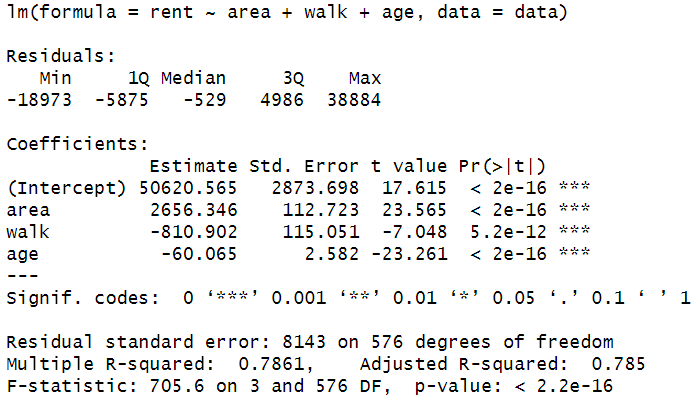
【回帰の有意性の検定】
$${F}$$値の$${p}$$値(p-value)は$${0.000 \cdots}$$です。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.000 \cdots}$$は有意水準より小さいので、帰無仮説を棄却できます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、この回帰モデルは有意である(偏回帰係数のどれかは目的変数に影響を与える)と言えます。
【回帰係数の有意性の検定】
各回帰係数の$${t}$$値の$${p}$$値(Pr(>| t |))は$${0.000 \cdots}$$です。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.000 \cdots}$$は有意水準より小さいので、帰無仮説を棄却できます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却され、すべての偏回帰係数は有意である(全ての回帰係数は目的変数に影響を与える)と言えます。
⑥ 分散分析の実行
最後のコードです。
回帰分析の結果 data.lm を読み込んで、anova を実行します。
### 分散分析の実施と結果表示
anova(data.lm)【実行結果】
分散分析表が表示されました。

Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイルをダウンロードできます。
以上で本記事の重回帰分析&分散分析を完了いたします。
最終回までお付き合いしてくださり、誠にありがとうございました。
おわりに
「統計検定2級公式問題集-CBT対応版」の分野・項目別の問題の全てを解きました。
長旅にお付き合いいただきまして、誠にありがとうございます。
一緒に旅を続けてくださった方はきっと、統計の基礎を体感して、面白さ、大切さに触れたことでしょう。
これから続く皆様の人生において、統計的視点が役に立つことを願ってやみません。
いつでも記事に戻ってきてくださいね。
Keep on 「のんびり統計」!
最後までお読みいただきまして、ありがとうございました。
それでは失礼いたします。
のんびり統計シリーズの記事
次の記事

前の記事
目次
