
1-9 コレログラムの選択 〜 時系列データの周期性を可視化
今回の統計トピック
時系列データ特有の「自己相関関数」を計算して、コレログラムを作成します。
時系列データの周期性と自己相関関数&コレログラムの関係に迫ります!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
1変数記述統計の分野
問9 コレログラムの選択(月別製品ガス販売量の時系列データ)
試験実施年月
統計検定2級 2019年11月 問5(回答番号9)
問題
公式問題集をご参照ください。
解き方
※時系列データ、コレログラム等の詳しい内容は「知る」の章に書きます。
時系列データのグラフの特徴
時系列に並んだガス販売量のグラフには、次の特徴が見られます。
毎年1月を上のピークとする12ヶ月周期の規則的な変動が見られます。
下のピークは5~7月くらいであり、6月ごろに小さな山があります。

時系列データとコレログラム
コレログラムは、大きなグラフの時系列データ全体を「1か月ずらしたラグ1」、「2か月ずらしたラグ2」というように、同じデータの時点をずらして、元データとラグ1データ、元データとラグ2といった具合に、ずらした時間軸の中に見られるデータ(の自己相関)の様子を可視化するものです。
コレログラムの推測
1つ目の12か月周期が見られることから、コレログラムはラグ12とラグ24で強い正の相関があると考えられます。
元のデータのグラフと12か月ずらしたグラフ、24か月ずらしたグラフは類似することでしょう。

2つ目の5~7か月後の谷と小さな山が見られることから、コレログラムはラグ5からラグ7、ラグ17からラグ19あたりに強い負の相関があって、ラグ6とラグ18は負の相関が少し弱まると考えられます。
元のデータのグラフと6か月ずらしたグラフ、18か月ずらしたグラフは、グラフの山と谷が逆転することでしょう。
選択肢のコレログラムを探る
この特徴に合致するコレログラムの選択肢は「②」です。
ラグ12とラグ24の自己相関(ACF)は大きな正の値です。
ラグ5~7、ラグ17~19の自己相関(ACF)は大きな負の値です。
ラグ6、ラグ18は前後のラグと比べると、少し負の値が小さくなっていて、小さな山があります。

他のコレログラムの選択肢を見てみましょう。
①はラグ12に強い負の相関があるので該当しません。
③はラグ12とラグ24に強い正の相関が見られるものの、ラグ5~7、ラグ17~ラグ19が正の相関になっているので、該当しません。
④は強い正の相関がラグ6、ラグ12・・・と6か月周期の動きがあり、該当しません。
⑤はラグ12に強い負の相関があり、該当しません。
解答
②です。
難易度 ふつう
・知識:時系列データ、コレログラム、自己相関
・計算力:不要
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
ここでは、「ガス事業生産動態統計調査」の2015年1月から2021年12月までの「月別製品ガス販売量データ」を利用します。
該当年月の「月次総括表」に記載の「製品ガス販売量計」の値を使用します。
【出典記載】
出典:「ガス事業生産動態統計調査」(経済産業省資源エネルギー庁)の「ガス事業統計年報」(暦年ベースの総括表)
【コンテンツ編集・加工の記載】
記事の記載にあたっては、「ガス事業生産動態統計調査」(経済産業省資源エネルギー庁)を加工して作成しています。
今回は時系列データ、コレログラム、自己相関関数に取り組みます。

時系列データ
📕公式テキスト:1.7.1 時系列データ(39ページ~)
時系列データのグラフを見る
「月別製品ガス販売量データ」を時間軸の順に並べてプロットしたグラフを見てみましょう。

公式問題集と同じように、12か月のサイクルで、1月が上のピーク、夏にかけて販売量が少なくなり、夏に少し山があり、冬にかけて販売量が多くなっています。
時系列データの周期性を見る
12か月の周期性をグラフで確認してみましょう。
素のデータ(原系列:青)、6か月ずらしたラグ6(緑),12か月ずらしたラグ12(赤)のグラフを重ねてみました。

原系列(青)とラグ12(赤)のグラフはよく似ていて、グラフが重なります。
両者には正の相関の関係がありそうです。
一方で、ラグ6(緑)のグラフは、原系列(青)やラグ12(赤)の反対の動きをしています。
ラグ6と原系列は負の相関の関係がありそうです。
ラグの正体
1か月ずらす、2か月ずらすの正体を明かします。
素のデータ(原系列データ)のコピーを、ラグの月の分だけずらして貼り付けするイメージです。

2015年2月の原系列データと対比するラグ1のデータは、2015年1月(つまり1か月ずらし)の値になります。
地道にコピペしました。鉄道運賃表に似てますね。

コレログラム
📕公式テキスト:1.7.4 自己相関(46ページ)
コレログラムを見る
「月別製品ガス販売量データ」のラグ0~ラグ30のコレログラムです。

きれいな周期性が見えます。
グラフの縦軸
コレログラムの縦軸は自己相関関数(ACF)です。
原系列データと各ラグデータとの間の「自己相関」の値です。
自己相関関数については次の項で取り扱うので、ここでは雰囲気を味わってください。
コレログラムを読んでみる
原系列データの気持ちになってみます。
ラグ1データとの関係は2015年2月始まりで、ラグ2データとの関係は同年3月始まりで取り扱います。このときはまだ正の相関を保ちます。
同年4月始まりで関係を扱うラグ3になって以降、同年10月始まりで扱うラグ9まで負の相関です。
そして、同年11月始まりで扱うラグ10から正の相関になり、2016年1月始まりを扱うラグ12が正の相関のピークになっています。
周期性を振り返る
原系列・ラグ6・ラグ12の時系列データ対比で見えた周期性が、コレログラムで「一定のリズムを思わせる」きれいな周期性を確認できたことにより、いっそう明確になりました。

自己相関関数
📕公式テキスト:1.7.4 自己相関(45ページ~)
ひとまず計算式です。
ここでは公式テキストにならって、自己共分散関数を用いた自己相関係数の計算式を記載します。
自己共分散関数(公式テキスト)
$$
C_h = \cfrac{1}{T} \displaystyle \sum^{T-h}_{t=1} (y_t-\bar{y})(y_{t+h}-\bar{y}),\quad h=0,1,2,\cdots
$$
自己共分散関数(よく見る式)
ネットではこちらの式をよく見かけます。
ラグの表記は、$${h}$$の代わりに$${k}$$を使っている式も多いです。
$$
C_h = \cfrac{1}{T} \displaystyle \sum^{T}_{t=h+1} (y_t-\bar{y})(y_{t-h}-\bar{y}),\quad h=0,1,2,\cdots
$$
自己相関関数:自己共分散関数を利用
$$
r_h=\cfrac{C_h}{C_0}
$$
自己共分散関数・自己相関関数の各要素を簡単に説明します。
$$
\begin{align*}
&【よく見る式をベースにしています】\\
&T : データの個数(84個)\\
&\bar{y} : データ平均(84か月の平均)\\
&h : ラグの値、ラグ1はh=1、ラグ2はh=2\\
&y_t : 原系列データ\\
&y_{t-h} : ラグデータ\\
&t=h+1とT : データをラグh分ずらした時点から開始して\\
&最後の時点Tまで\sumの計算を実施\\
&※ラグh=1の場合は、データの時点の2番目から84番目までの\\
&全83個のデータを対象にして、(y_t-\bar{y})(y_{t+h}-\bar{y})の計算を実施\\
&C_0 : 全データ(84か月)の分散
\end{align*}
$$
自己相関関数を計算してイメージする
簡易なデータ例で自己相関関数の計算過程を追いかけます。
「よく見る式」で書いてみます。
■データ例
時間1ステップごとに、値1と4が交互に現れています。
周期性があります。
データyの平均$${\bar{y}}$$と分散$${\sigma^2_y=C_0}$$は自己相関関数の計算に用います。

はじめに自己相関関数とコレログラムを押さえてみましょう。
時間軸が1つずつずれる(ラグが1つずつ増える)ごとに、正の値と負の値が交互に入れ替わります。

■ケース:ラグ0

【表と数式の関係】
時間t:計算式の$${t}$$(計算式の$${T}$$は5になります)
データy:$${(y_t-\bar{y})}$$の$${y_t}$$
ラグ0等:$${(y_{t-h}-\bar{y})}$$の$${y_{t-h}}$$($${h}$$はラグです)
(データy-平均):$${(y_t-\bar{y})}$$
(ラグ0等-平均):$${(y_{t-h}-\bar{y})}$$
掛け算:$${(y_t-\bar{y})(y_{t-h}-\bar{y})}$$
合計Σ:$${\sum^{T}_{t=h+1} (y_t-\bar{y})(y_{t-h}-\bar{y})}$$(掛け算列の合計です)
×1/5:$${1/T}$$(合計Σに1/5を掛けています)
÷分散:自己相関関数$${r_h=C_h/C_0}$$(×1/5を分散で割っています)
ラグ0データは素のデータと同じなので、自己相関関数は「1」です。
折れ線グラフで並べてみると、ぴったり一致します。
強い正の相関です。

■ケース:ラグ1
時間軸を1つずらすと、真逆の動きになります。
強い負の相関です。


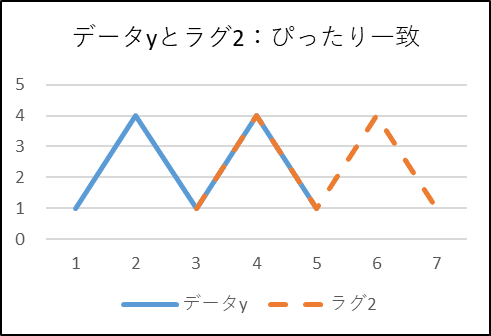
■ケース:ラグ2
ラグ2ではぴったり一致します。
正の相関です。
計算に使われるデータの数が減っていることに注目します。
しかし、×1/5(計算式の$${1/T}$$)は変わりません。
この結果、ラグ0と比べて、自己相関関数の正の値は小さくなります。

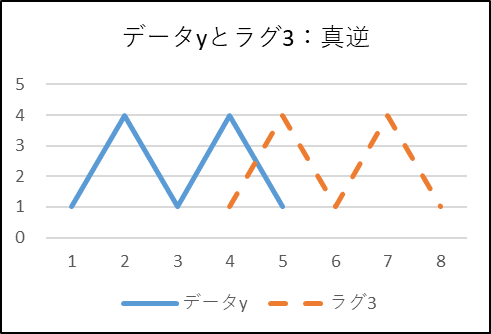
■ケース:ラグ3
ラグ3では真逆の動きになります。
負の相関です。
計算に使われるデータの数が減っていることに注目します。
しかし、×1/5(計算式の$${1/T}$$)は変わりません。
この結果、ラグ1と比べて、自己相関関数の負の値は小さくなります。

自己相関関数が正/負になる訳
項目「(データy-平均)」と項目「(ラグh-平均)」の+/-の符号に注目しましょう。
この2つの項目は、データと平均の差です。
値が+になるのは、平均よりも大きい場合です。
値が-になるのは、平均よりも小さい場合です。
両方が+の場合、両方のデータは「平均よりも大きいというデータの方向性が同じ」であり、両方のデータを掛け合わせると+の値になります。
両方が-の場合、両方のデータは「平均よりも小さいというデータの方向性が同じ」であり、両方のデータを掛け合わせると+の値になります。
一方が+で他方が-の場合、両方のデータは「一方は平均よりも大きく、他方は平均よりも小さく、データの方向性が異なる」のであり、両方のデータを掛け合わせると-の値になります。

ざっくりまとめ
ざっくりまとめると次のようになります。
■相関の正/負
平均との差の+/-が同じ → 正の相関になりやすい
平均との差の+/-が違う → 負の相関になりやすい
■相関の強さ
また、平均との差の大きさが、相関の強さに関わります。
平均との差が大きい → 掛け算の結果も大きい → 相関が強い方向に影響(正の場合は +1 に近づく/負の場合は -1 に近づく)
平均との差が小さい → 掛け算の結果も小さい → 相関が弱い方向に影響(0に近づく)
■ラグの大きさと自己相関関数の値
さらに、ラグが大きくなるにつれて、自己相関関数の値は減衰します。
計算の網にかかるデータ数がどんどん減っているのに対して、「×1/5(計算式の$${1/T}$$)の値が一定(減らない)」ことが効いています。
おまけ:相関係数と自己相関関数
📕公式テキスト:1.6.2 相関係数(29ページ~)
(注)ここでは「標本」の概念を用いないで説明します。
主要な統計量に「相関係数」があります。
ピアソンの積率相関係数と呼ばれるものです。
相関係数は「2つの変数の共分散」を「それぞれの変数の標準偏差を掛けたもの」で割って求めます。
$$
\begin{align*}
&xとyの共分散\ S_{xy}\\
&=\cfrac{1}{n} \{ (x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots +(x_n-\bar{x})(y_n-\bar{y})\}\\
&=\cfrac{1}{n} \sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y})
\end{align*}
$$
$$
相関係数r_{xy}=\cfrac{s_{xy}}{s_x s_y} \quad (s_x:xの標準偏差,\ s_y:yの標準偏差)
$$
自己共分散関数、自己相関関数の計算式によく似ています。
自己共分散関数(よく見る式)
$$
C_h = \cfrac{1}{T} \displaystyle \sum^{T}_{t=h+1} (y_t-\bar{y})(y_{t-h}-\bar{y}),\quad h=0,1,2,\cdots
$$
自己相関関数
$$
r_h=\cfrac{C_h}{C_0} \quad (C_0はデータyの分散\sigma^2_y)
$$

主な違いは2点。
1点目は、引き算する平均$${\boldsymbol{\bar{y}}}$$です。
相関係数では、データ$${x}$$の平均は$${\bar{x}}$$、データ$${y}$$の平均は$${\bar{y}}$$というように、データごとに平均をとっています。
一方で自己相関関数では、データ$${y}$$全体の平均$${\bar{y}}$$を共通的に引いています。
$${y_t}$$の平均、$${y_{t-h}}$$の平均を用いていません。
2点目は、冒頭で掛け算する$${\boldsymbol{1/T}}$$です。
相関係数では、データ数$${n}$$を使用します。
一方で自己相関関数では、データ$${y}$$全体の個数$${T}$$を使用します。
たとえば、データ数が$${T=5}$$でラグが$${h=2}$$の場合、$${5-2=3}$$個のデータで計算しますが、冒頭の掛け算は$${1/3}$$ではなく、$${1/5}$$です。
自己相関関数はラグが大きくなるにつれて減衰する傾向がありますが、相関係数は減衰しにくいです。
実践する
自己相関関数を計算してコレログラムを描いてみよう
「月別製品ガス販売量データ」は資源エネルギー庁のホームページで公開されています。
「調査の結果(ガス事業生産動態統計調査)」のページで各種調査結果をダウンロードできます。
2015年1月から2021年12月までの「月別製品ガス販売量データ」は、各年の「総括表(1~12月)」EXCELファイル中、各月の「月次総括表」の「製品ガス・販売量・計」欄の値(単位:1000メガジュール)です。
CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。
【出典記載】
出典:「ガス事業生産動態統計調査」(経済産業省資源エネルギー庁)の「ガス事業統計年報」(暦年ベースの総括表:2015年~2021年分)
電卓・手作業で作成してみよう!
上述の方法でデータを取得して計算してみましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
でも、大量のデータを用いて自己相関関数を求めるのはきついですよね。
「自己相関関数を計算してイメージする」の「簡易なデータ例」を用いて、自己相関関数を計算して、コレログラムを描画するのがいいかもしれません。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
自己相関関数の計算
EXCELには自己相関関数を求める関数がなさそうです。
データ数が多い場合、自己相関関数の計算式を組むのは大変そうです。。。
相関係数で代用する
厳密に言えば、自己相関関数と相関係数は異なります。
自己相関関数に似た数字という割り切りのもとで、相関係数を計算してみましょう。
EXCELのCORREL関数を利用します。
引数に「原系列データ」と「ラグデータ」の範囲を指定します。
隣合わせのペアの値が無い部分は、相関係数の計算の対象外になるようです。

コレログラム(風)のイメージ
上図のEXCELの2行目と3行目を利用してコレログラム(風)を「棒グラフ」で作成しました。
EXCELのCORREL関数で求める相関係数は、ラグが大きくなっても、値が小さくなりにくい(減衰しにくい)です。

「EXCELのCORREL関数で算出」の場合の棒グラフの範囲指定の例です。
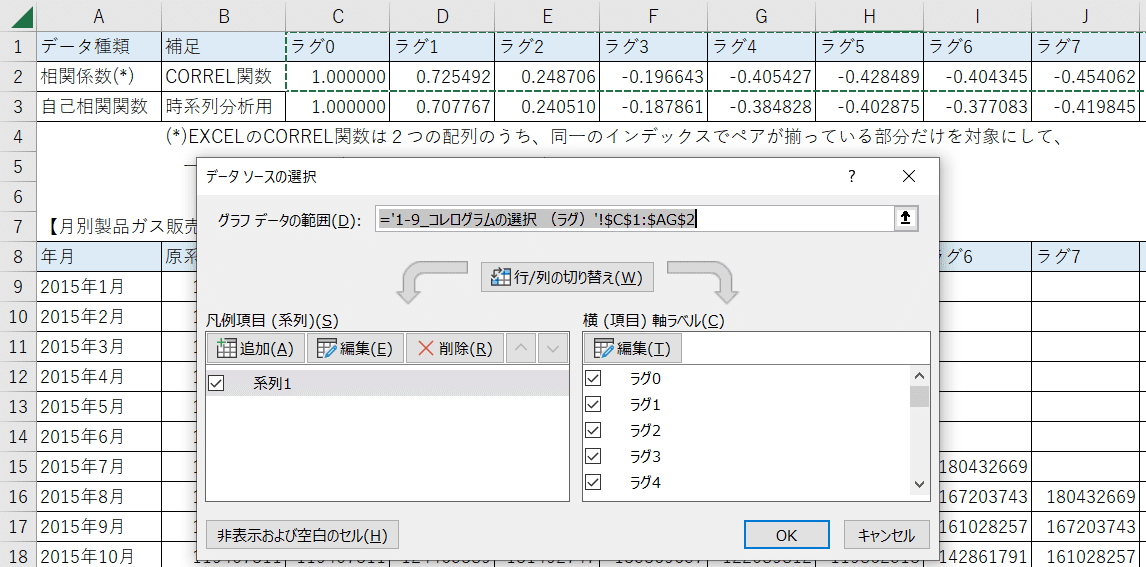
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は自己相関関数の計算とコレログラムの描画に取り組んでみましょう。
「1-5 時系列の変動の性質」で描画した変動分解のグラフ、コレログラムのコードも利用します。
①ライブラリのインポート
statsmodelsに含まれる時系列分析関連のモジュールを使用します。
import pandas as pd
import numpy as np
from statsmodels.tsa.stattools import acf
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。
datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile,
dtype = {'販売量':'float'},
index_col='年月', # '年月'をインデックスに設定
parse_dates=True)
print(df.shape)
display(df.head())③自己相関関数の計算
「公式テキストの式」、「よく見る式」、「statsmodelのacf」で計算します。
自己共分散関数と自己相関関数のコードは次のサイトを参考にしました。
ありがとうございます!
■公式テキストの式
# 公式テキストの式
# 自己共分散関数の定義
def auto_cov_text(h, y):
y_mean = np.mean(y)
T = len(y)
return (1/T) * np.sum([(y[t] - y_mean) * (y[t+h] - y_mean) for t in range(0, T-h)])
# 自己相関関数の定義
def auto_coef_text(h, y):
return auto_cov_text(h, y) / auto_cov_text(0, y)
# 自己相関関数の計算
lags = 30
acf_text = [auto_coef_text(i, df.values) for i in range(lags+1)]
print(np.array(acf_text)
出力イメージ
[ 1. 0.7077669 0.24051009 -0.18786137 -0.38482755 -0.40287543
-0.37708286 -0.41984524 -0.39740163 -0.18925605 0.2067804 0.60930601
0.77725535 0.54187567 0.15948383 -0.18424256 -0.33919509 -0.36142172
-0.33569976 -0.36082299 -0.31288803 -0.14240225 0.18252599 0.50455418
0.64056743 0.43733583 0.11613931 -0.17704416 -0.30815489 -0.31834203
-0.29255312]■よく見る式
# よく見る式
# 自己共分散関数の定義
def auto_cov_gen(k, y):
y_mean = np.mean(y)
T = len(y)
return (1/T) * np.sum([(y[t] - y_mean) * (y[t-k] - y_mean) for t in range(k, T)])
# 自己相関関数の定義
def auto_coef_gen(k, y):
return auto_cov_gen(k, y) / auto_cov_gen(0, y)
# 自己相関関数の計算
lags = 30
acf_gen = [auto_coef_gen(i, df.values) for i in range(lags+1)]
print(np.array(acf_gen))
出力イメージ
[ 1. 0.7077669 0.24051009 -0.18786137 -0.38482755 -0.40287543
-0.37708286 -0.41984524 -0.39740163 -0.18925605 0.2067804 0.60930601
0.77725535 0.54187567 0.15948383 -0.18424256 -0.33919509 -0.36142172
-0.33569976 -0.36082299 -0.31288803 -0.14240225 0.18252599 0.50455418
0.64056743 0.43733583 0.11613931 -0.17704416 -0.30815489 -0.31834203
-0.29255312]■statsmodelのacf
# statsmodelで自己相関関数を計算
lags = 30
acf_statsmodels = acf(df, nlags=lags)
print(acf_statsmodels)
出力イメージ
[ 1. 0.7077669 0.24051009 -0.18786137 -0.38482755 -0.40287543
-0.37708286 -0.41984524 -0.39740163 -0.18925605 0.2067804 0.60930601
0.77725535 0.54187567 0.15948383 -0.18424256 -0.33919509 -0.36142172
-0.33569976 -0.36082299 -0.31288803 -0.14240225 0.18252599 0.50455418
0.64056743 0.43733583 0.11613931 -0.17704416 -0.30815489 -0.31834203
-0.29255312]■3つの式の計算結果を比べる
# 公式テキストとよく見る式は同値
acf_text==acf_gen
出力イメージ
True# statsmodelは端数丸めをしている。非常に小さな差が生じる。
print(acf_text - acf_statsmodels)
出力イメージ
[ 0.00000000e+00 0.00000000e+00 2.77555756e-17 -2.77555756e-17
-5.55111512e-17 0.00000000e+00 0.00000000e+00 0.00000000e+00
5.55111512e-17 0.00000000e+00 5.55111512e-17 -1.11022302e-16
1.11022302e-16 0.00000000e+00 2.77555756e-17 0.00000000e+00
5.55111512e-17 5.55111512e-17 0.00000000e+00 -1.66533454e-16
5.55111512e-17 5.55111512e-17 2.77555756e-17 1.11022302e-16
1.11022302e-16 0.00000000e+00 0.00000000e+00 2.77555756e-17
-5.55111512e-17 -5.55111512e-17 5.55111512e-17]④時系列推移グラフの表示
matplotlibのplotで折れ線グラフをプロットします。
plt.figure(figsize=(7, 3))
plt.plot(df.index, df.values)
plt.grid(axis='x', color='gray', linewidth=0.5, linestyle=':')
plt.xticks(['2015年12月', '2016年12月', '2017年12月', '2018年12月',
'2019年12月', '2020年12月', '2021年12月'],
rotation=30)
plt.title('月別製品ガス販売量の推移')
plt.ylabel('販売量(1000億メガジュール)')
plt.tight_layout()
# plt.savefig('./plot.png') # グラフ画像ファイルの保存
plt.show()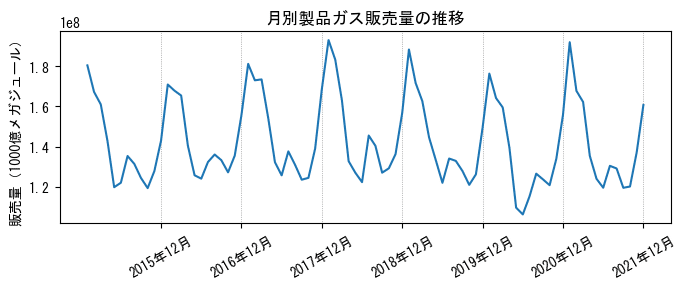
⑤コレログラムの表示1
statsmodelsの自己相関関数acf_statsmodelsを使用して棒グラフをプロットします。
SciPyのinterp1dを使用してコレログラムの頂点を通る近似曲線をプロットします。
# x軸 ラグの設定
x_lag = np.linspace(0, 30, 31)
# 近似曲線の設定
x_cubic_curve = np.linspace(0, 30, 100)
cubic_curve = interp1d(x_lag, acf_statsmodels, kind='cubic')
plt.figure(figsize=(7, 3))
plt.ylim(-1.1, 1.1)
# プロット
plt.axhline(y=0, linewidth=0.5, color='black', linestyle=':')
plt.bar(x_lag, acf_statsmodels, width=0.2, color='steelblue')
plt.plot(x_cubic_curve, cubic_curve(x_cubic_curve),
linewidth=0.5, color='navy', linestyle='--')
# 修飾
plt.title('コレログラム:2015年1月~2021年12月の月別製品ガス販売量')
plt.xlabel('ラグ')
plt.ylabel('自己相関関数 ACF')
plt.tight_layout()
# plt.savefig('./correlogram1.png') # グラフ画像ファイルの保存
plt.show()
⑥変動分解
「1-5 時系列の変動の性質」のコードを利用します。
傾向変動(循環変動を含む)、季節変動(1年周期)、不規則変動に分解してプロットします。
statsmodelsのseasonal_decomposeを利用します。
# 変動分解(移動平均による加法モデル)
result=seasonal_decompose(df['販売量'], model='additive', period=12)
# この2行だけでプロットを表示可能
# result.plot()
# plt.show()
fig, ax = plt.subplots(nrows=4, ncols=1, figsize=(7, 8), sharex=True)
# 原系列のプロット
ax[0].set_title('Observed:原系列')
ax[0].plot(result.observed, lw=0.5)
ax[0].set_xticks(['2015年12月', '2016年12月', '2017年12月', '2018年12月',
'2019年12月', '2020年12月', '2021年12月'])
# 傾向変動のプロット
ax[1].set_title('Trend:傾向変動')
ax[1].plot(result.trend, lw=0.5)
# 季節変動のプロット
ax[2].set_title('Seasonal:季節変動')
ax[2].plot(result.seasonal, lw=0.5)
# 不規則変動のプロット
ax[3].set_title('Residual:不規則変動')
ax[3].scatter(result.resid.index, result.resid.values, s=2)
plt.axhline(y=0, lw=0.5)
plt.tight_layout()
# plt.savefig('./ts_tsi.png') # グラフ画像ファイルの保存
plt.show()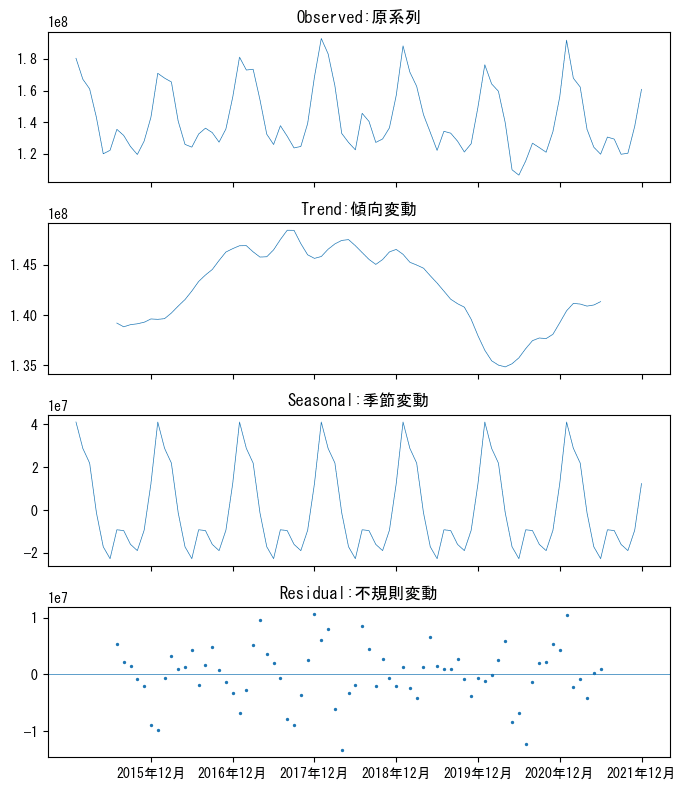
⑦コレログラムの表示2
「1-5 時系列の変動の性質」のコードを利用します。statsmodels.graphics.tsaplotsを使用して作成します。
plot_acf : コレログラム(自己相関係数)
plot_pacf : 偏自己相関係数
lags = 30
fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1, figsize=(7, 5),
sharex=True, sharey=True)
ax1.set_ylim(-1.5, 1.5)
ax1 = plot_acf(df['販売量'], lags=lags, ax=ax1,
title='コレログラム(自己相関係数)')
ax2 = plot_pacf(df['販売量'], lags=lags, ax=ax2, method='ywm',
title='偏自己相関係数')
plt.tight_layout()
# plt.savefig('./correlogram2.png') # グラフ画像ファイルの保存
plt.show()
■グラフを読んでみて
⑥変動分解のTrend(傾向変動)を見ると、2020年上半期のガス販売量が大きく下方に落ち込んでいます。
新型ウィルスの緊急事態宣言が発令されて「工場の休止や店舗の休業で都市ガス需要や発電用LNG需要が大幅に減少した(*)」ことが、可視化したトレンド(傾向変動)に現れています。
コロナ禍は、1年を超える傾向にくっきりと現れるほどの長期にわたって、ガス販売量の減少という経済的なインパクトをもたらした、と言えそうです。
(*)「石油・天然ガス資源情報ウェブサイト」の「天然ガス・LNGをめぐる動向 (2020年)」より引用
時系列データ特有の分析方法をいろいろと学んでいきたいですね。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
今回は時系列データの推移グラフとコレログラムを読み解く問題にチャレンジしました。
実のところ、個人的に時系列分析の問題が苦手でして、この問題もよく間違えました。
時系列データに見られる「周期性」が、どのようにコレログラム(自己相関関数)にリンクするのか、想像が及ばなかったのです。
この記事を書くにあたって、(パソコンの力を借りて)実際にグラフを描いたり、具体的な数値を使って自己相関関数を計算したりして、ちょっぴり時系列分析の扉に近づけた気がします。
いい経験になりました。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
