
第15章「物理を学べば船が水に浮かぶ理由を説明できる?」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第15章「物理を学べば船が水に浮かぶ理由を説明できる?」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
今回も章タイトルのインパクトが強いですね!
この章では、「浮力」を題材にして「知識や公式を丸暗記するのではなく、意味を理解して説明できることが必要ではないか」という学びのギモンをベイズで分析します。

今回の PyMC化 は、テキストの結果と概ね一致しました!
ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 松浦拓也 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
テキストのStanコード「Mu02.stan」の初見時に「これをPyMC化するのは厄介だよな~」と弱気になりました。。。
コードに含まれる複数の要素を1つ1つコツコツと分解していく中で、「難易度の高い変数をPyMCモデルの外で計算する方針」を決めることができました。
外に出した難しい変数を除くと、コードがシンプルな変数を使っていることに気付き、完成したPyMCモデルはめっちゃシンプルになりました。
難しいことを難しいまま対処するのではなく、自分にとって理解可能なレベルに簡単化することが大切だなと感じた章でした。
工夫・喜び・反省
$${a \times b}$$のクロス集計表を観測データとして扱うベイズモデルが面白かったです。
集計表の相関を見る手法として「クラメルの連関係数$${V}$$」と「ピアソン残差$${e_{ij}}$$」を学ぶことができました。

モデルの概要
テキストの調査・実験の概要
■ 先生の問題意識
この章の問題意識をテキストから引用いたします。
たとえば、理科の勉強をしていると、「知識や公式などを単に丸暗記するのではなく、その意味を理解したり、説明したりできるようになることが大切だ」などとアドバイス(小言?)をされることはないだろうか。何となく、もっともらしい言説に聞こえるように思えるけど、果たして本当なのだろうか。おそらく、新しい問題場面に遭遇した際、理科で学んだ知識や法則などを演繹的に用いて自力で解決できるようになるためには、公式などを暗記しただけでは不十分であると考えているからこそ、このようなアドバイスをするのだと思われる。しかし、この考えは正しいのだろうか?
筆者の先生はこの疑問「丸暗記と意味理解の相違」を「浮力」で探ります。
■ 浮力の4つの出題
浮力$${F}$$は水の密度$${\rho}$$、物体の体積$${V}$$、重力加速度$${g}$$を用いて公式化されます。
$$
F=\rho Vg
$$

調査では、111名の理系大学生に浮力に関する4つの問題を出題しています。
問題(4)が浮力そのものの説明です。丸暗記でなく、意味を理解したり他者に説明できるかを問う問題です。
問題(3)が重たい船が水に浮かぶ理由の説明です。浮力の意味の理解を問う問題のようです。
問題(1)と(2)が浮力が関わる応用問題です。こちらも浮力の意味の理解を問う問題のようです。
そして次の2点をベイズ分析して、理解度と応用力の関係を探ります。
応用問題(1)(2)の正答/誤答と、浮力理解(問題(4))の正答/誤答
船が水に浮かぶ理由(問題(3))の正答/誤答と、浮力理解(問題(4))の正答/誤答
仮説的には、意味理解が高い人ほど応用問題を正しく説明できる、でしょう。
ここまでの概要を図にしました。
出題問題の詳細はぜひテキストでご確認ください!

テキストのモデリング
1.問題(1)(2)と問題(4)のクロス集計表のモデル
■ 目的変数と関心のあるパラメータ
目的変数は回答のクロス集計表の各セル値$${x_{ij}}$$です。
関心のあるパラメータはクラメルの連関係数$${V}$$とピアソン残差$${e_{ij}}$$です。
添字$${i}$$はクロス集計表の縦軸を、$${j}$$はクロス集計表の横軸を示します。
■ モデル数式
確率パラメータにクロス集計表の各セルの母比率$${p_{ij}}$$を用いる多項分布モデルです。
$$
x_{ij} \sim \text{Multinomial}\ (p_{ij})
$$
2.問題(3)と問題(4)のクロス集計表のモデル
■ 目的変数と関心のあるパラメータ
1.のモデルと同様です。
■ モデル数式
1.のモデルと同様です。
◆ ◆ ◆ ◆ ◆
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
from semopy.polycorr import hetcor
# PyMC
import pymc as pm
import arviz as az
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込みと前処理
csvファイル「data_matsuura.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
data = pd.read_csv('data_matsuura.csv')
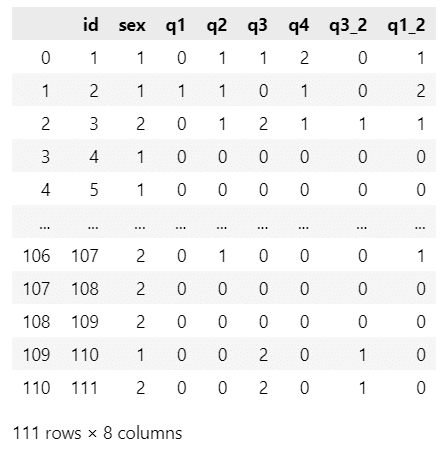
display(data)【実行結果】
111名の回答データです。
項目内容の概要です。
・id:回答者ID
・sex:回答者の性別
・q1~q2:問題(1)および問題(2)について、正答:1、誤答:0
・q3:問題(3)について誤答その他:0、誤答公式のみ:1、正答(密度):2、正答(浮力):3
・q4:問題(4)について誤答:0、上下水圧差のみ:1、公式のみ:2、正答:3
・q3_2:問題3について誤答:0、正答:1
・q1_2:q1+q2
3.データの概観の確認
要約統計量を確認しましょう。
### 要約統計量の表示
display(data.describe().round(3))【実行結果】
問題(1)~(4)の中央値はすべて0。
半数の参加者は正答できなかったようです。

テキスト表15.1の記述統計量を算出します。
### 記述統計量の算出 ※表15.1に相当
## 初期値設定
# 設問名
title = {'q1': '問題(1)応用', 'q2': '問題(2)応用', 'q3': '問題(3)船',
'q4': '問題(4)浮力'}
# 解答類型名
subtitle = {'q1': {0: '誤答', 1: '正答'}, 'q2': {0: '誤答', 1: '正答'},
'q3': {0: '誤答:その他', 1: '誤答:公式のみ',
2: '正答:密度に基づく説明', 3: '正答:浮力に基づく説明'},
'q4': {0: '誤答', 1: '上下水圧差のみ', 2: '公式のみ', 3: '正答'}}
## value_counts()で度数・比率を算出してデータ1行を作成する関数の定義
def get_row(col, num):
# 人数の算出
val_count = data[col].value_counts().loc[num]
# 比率(%)の算出
val_ratio = data[col].value_counts(normalize=True).loc[num]
# 戻り値:設問名、解答類型名、人数、%
return title[col], subtitle[col][num], val_count, round(val_ratio*100, 1)
## データフレーム化
# 設問番号・解答類型番号ごとに度数・比率の行を作成してデータフレーム化
stats_df01 = pd.DataFrame(
[get_row('q1', 1), get_row('q1', 0),
get_row('q2', 1), get_row('q2', 0),
get_row('q3', 3), get_row('q3', 2), get_row('q3', 1), get_row('q3', 0),
get_row('q4', 3), get_row('q4', 2), get_row('q4', 1), get_row('q4', 0)],
columns=['設問', '解答類型', '人数', '%'])
# データフレームの表示
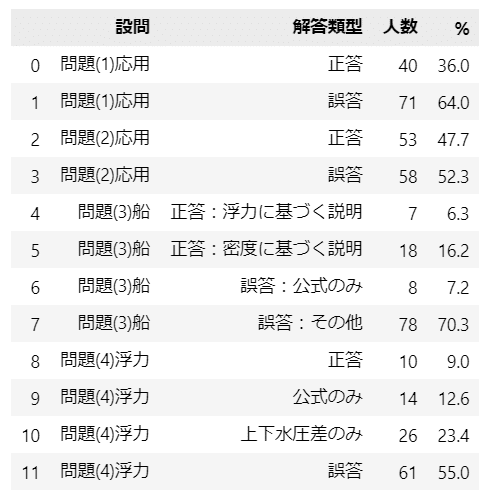
display(stats_df01)【実行結果】
浮力の問題は難しかったのでしょうか・・・
■ テトラコリック相関
テキストにならってテトラコリック相関を算出しましょう。
表15.2に相当します。
ところで「テトラコリック相関」、初めて知ったワードです。
二値変数間の相関係数だそうです。
構造化方程式モデリングの semopy にテトラコリック相関を算出できる関数 hector があります。
### テトラコリック相関の表示 ※表15.2に相当
# https://semopy.com/docs/polycorr.html#semopy.polycorr.hetcor
# 行・列見出しのリスト作成
title2 = ['問題(1)', '問題(2)', '問題(3)']
# hetcor()でテトラコリック相関を算出してデータフレーム化
stats_df02 = pd.DataFrame(hetcor(data.iloc[:, [2, 3, 6]].to_numpy()),
index=title2, columns=title2)
# データフレームの表示
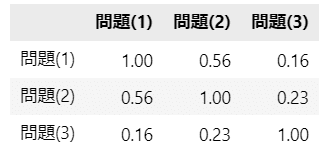
display(stats_df02.round(2))【実行結果】
問題(1)と(2)が中程度の相関です。
テキストはこの相関を確認の上、問題(1)と問題(2)を合算することにしています。

モデル1:問題(4)と問題(1)(2)
このモデルに投入するクロス集計表を作成します。
出力結果はテキストの表15.5に相当します。
### 問題(4)と問題(1)・(2)のクロス集計表の表示 ※表15.5に相当
# データ加工用に一時データフレームを作成
data_tmp = data.copy()
# 問題(4)の値に回答類型名を設定
subtitle2 = ['d.誤答', 'c.上下水圧差のみ', 'b.公式のみ', 'a.正答']
data_tmp['q4'] = data_tmp['q4'].apply(lambda x: subtitle2[x])
# 問題(1)(2)合計の値に「点」を付与
data_tmp['q1_2'] = data_tmp['q1_2'].apply(lambda x: f'{x}点')
# 列名の変更
data_tmp.rename(columns={'q4': '問題(4)', 'q1_2': '問題(1)(2)合計'}, inplace=True)
# 問題(4)と問題(1)(2)合計のピボットテーブルの作成
stats_df11 = data_tmp.pivot_table(index='問題(4)', columns='問題(1)(2)合計',
values='id', aggfunc='count',
margins=True, margins_name='計')
# ピボットテーブルの表示
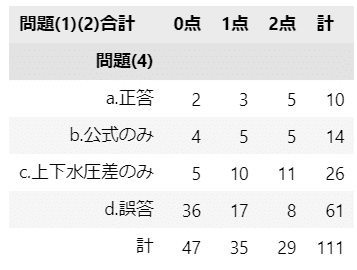
display(stats_df11)【実行結果】
計欄を除いたクロス集計表の各セルを観測値といたします。
ぱっと見で、問題(4)を誤答の場合、問題(1)(2)の合計点は0が多いですね。
丸暗記は応用が効かない、のかもです。
モデルの数式表現
目指したいPyMCのモデルの「なんちゃって数式」表記です。
$${N1}$$はクロス集計表の総計 111 です。
ディリクレ分布の引数$${\text{a}}$$には$${4\times3=12}$$の1が並んでいます。
$$
\begin{align*}
p &\sim \text{Dirichlet}\ (\text{a}=(1,1,\cdots, 1)) \\
likelihood &\sim \text{Multinomial}\ (\text{n}=N1,\ \text{p}=p) \\
\end{align*}
$$
1.モデルの定義
数式表現を実直にモデル記述します。
xv_data1は観測値であり、クロス集計表の各セルを平坦化したものです。
また、テキストの Stan コードではモデル内でクラメルの連関係数やピアソン残差などを計算していますが、このモデルでは計算していません。
### モデルの定義
## データの準備
# 目的変数:問題(4)と問題(1)(2)のクロス集計表を平坦化
xv_data1 = stats_df11.iloc[:4, :3].values.flatten()
# クロス集計表の合計
N1 = xv_data1.sum()
# 添字のリスト
suffix = [int(f'{i}{j}') for i in range(1, 5) for j in range(1, 4)]
## モデルの定義
with pm.Model() as model1:
## coordの定義
# データのインデックス
model1.add_coord('data', values=suffix, mutable=True)
## dataの定義
# 目的変数:クロス集計表の平坦化データ
x = pm.ConstantData('x', value=xv_data1, dims='data')
## 事前分布:確率合計1になるディリクレ分布
p = pm.Dirichlet('p', a=np.ones(len(xv_data1)), dims='data')
## 尤度:多項分布
likelihood = pm.Multinomial('likelihood', n=N1, p=p, observed=x,
dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の1つを設定しました。データの行の座標:名前「data」、値「行インデックス」
dataの定義
次の1つを設定しました。クロス集計表の各セル値:x (目的変数)
パラメータの事前分布
ディリクレ分布を用いて確率パラメータ$${p}$$の合計が1になるようにしています。
尤度
試行回数パラメータに回答者数、確率パラメータにクロス集計表の各セルの比率を持つ多項分布です。
2.モデルの外観の確認
### モデルの表示
model1【実行結果】
すごくシンプルです!

### モデルの可視化
pm.model_to_graphviz(model1)【実行結果】
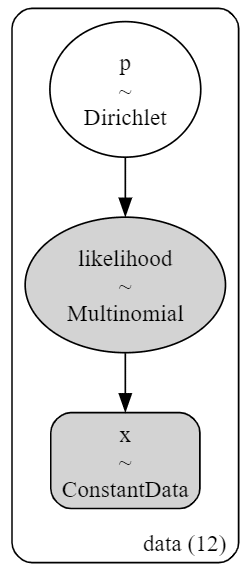
3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ10秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 10秒
# テキスト: iter=11000, warmup=1000, chains=5
with model1:
idata1 = pm.sample(draws=10000, tune=1000, chains=5, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata1 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata1, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata1, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.事後予測サンプリング
目的変数$${x}$$の事後予測からサンプリングします。
### 事後予測サンプリング
with model1:
idata1.extend(pm.sample_posterior_predictive(idata1, random_seed=1234))【実行結果】

事後予測プロットでモデルの予測を確認しましょう。
### 事後分布プロットの描画
pm.plot_ppc(idata1, num_pp_samples=100, random_seed=1234);【実行結果】
黒線の観測値とそこそこ近い?感触ということにしましょう。
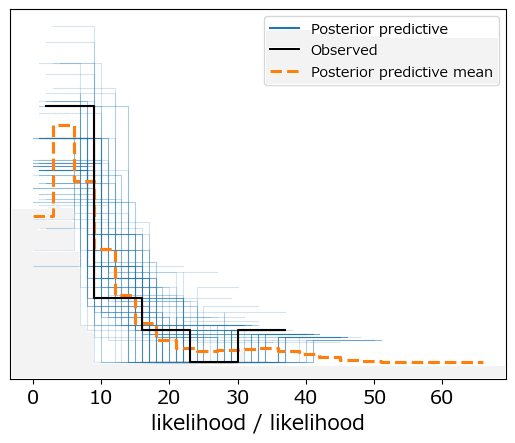
事後予測統計量を確認しましょう。
### 事後予測サンプリングの統計量の表示
pm.summary(idata1.posterior_predictive.likelihood, round_to=1)【実行結果】

6.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata1 をpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch15.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch15.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)
モデル1の分析
パラメータの事後統計量の算出関数の定義です。
### 事後分布等の統計量算出関数の定義, 共通変数の定義
# 関数の定義
def calc_stats1(x):
ci = np.quantile(x, q=[0.025, 0.975])
return np.mean(x), np.std(x), ci[0], np.median(x), ci[1]
# 列名の定義
colname = ['EAP', 'sd', '2.5%ci', 'MED', '97.5%ci']
# サンプル数
num_samples = 4000
# 行数a、列数b
a, b, = 4, 3
ab = a * b■ クロス集計表の母比率の事後統計量
クロス集計表の母比率$${p}$$の要約統計量を算出します。
テキストの図15.6上段に相当します。
### 問題(4)と問題(1)(2)のパラメータの事後分布の要約統計量の算出 ※表15.6上に相当
# 表示する変数名の一時リスト化 p11, p12, ・・・, p42, p43
tmp_names = [f'p{i+1}{j+1}' for i in range(a) for j in range(b)]
# 母比率pの事後分布サンプリングデータを取り出して一時変数に格納
tmp = idata1.posterior.p.stack(sample=('chain', 'draw')).data
# p(セルごと)に要約統計量算出を繰り返し処理して一時辞書に設定
tmp_dict = {}
for i in range(ab):
tmp_dict[tmp_names[i]] = calc_stats1(tmp[i])
# データフレーム化
stats_df12 = pd.DataFrame(tmp_dict, index=colname).T
# データフレームの表示
display(stats_df12.round(3))【実行結果】
テキストの結果とほぼ一致しています。
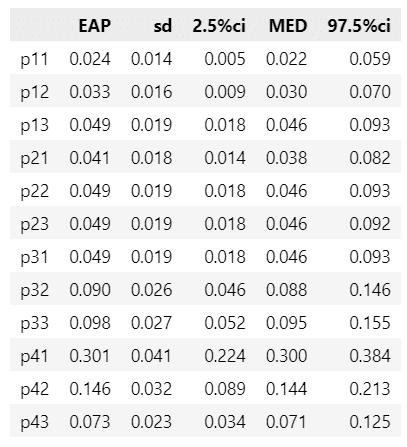
■ クロス集計表の値の事後予測統計量
続いてクロス集計表の値$${x}$$の要約統計量を算出します。
テキストの図15.6下段に相当します。
### 問題(4)と問題(1)(2)のパラメータの事後分布の要約統計量の算出 ※表15.6下に相当
# 表示する変数名の一時リスト化 x*11, x*12, ・・・, x*42, x*43
tmp_names = [f'x*{i+1}{j+1}' for i in range(a) for j in range(b)]
# 目的変数yの事後予測サンプリングデータを取り出し
tmp = idata1.posterior_predictive.likelihood.stack(sample=('chain', 'draw')).data
# x(セルごと)に要約統計量算出を繰り返し処理して一時辞書に設定
tmp_dict = {}
for i in range(ab):
tmp_dict[tmp_names[i]] = calc_stats1(tmp[i])
# データフレーム化
stats_df13 = pd.DataFrame(tmp_dict, index=colname).T
# データフレームの表示
display(stats_df13.round(1))【実行結果】
テキストの結果とほぼ一致しています。
事後平均値(EAP)は表15.5のクロス集計表の値に近いです。
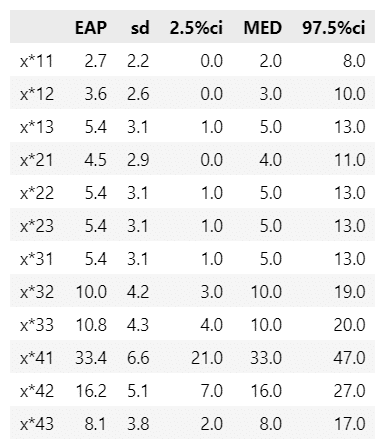
周辺確率、クラメルの連関係数、ピアソン残差を算出します。
テキストの Stan コード「Mu02.stan」の計算式を引用しております。
### 問題(4)と問題(1)(2)の周辺確率、ピアソン残差、クラメルの連関係数の算出
# 母比率pの事後分布サンプリングデータに基づいて上記統計量を計算します
## 周辺確率、ピアソン残差、クラメルの連関係数算出関数の定義
# テキストのMu02.stanファイルの計算式を引用しています
def calc_stats2(pi):
# 入力引数:母比率pの事後分布サンプリングデータ(1行)
# 変数の初期化
pa = np.zeros(a) # 周辺確率(行)
pb = np.zeros(b) # 周辺確率(列)
res = np.zeros((a, b)) # ピアソン残差
Up = np.zeros((a, b)) # ピアソン残差が正の場合1
Um = np.zeros((a, b)) # ピアソン残差が負の場合1
V = 0 # クラメルの連関係数
# 母比率pの入力引数(ベクトル形式)を行列形式に変換
pim = pi.reshape(a, b)
# 周辺確率の算出
for i in range(a):
for j in range(b):
pa[i] = pa[i] + pim[i, j]
pb[j] = pb[j] + pim[i, j]
# クラメルの連関係数とピアソン残差の算出
for i in range(a):
for j in range(b):
res[i, j] = (pim[i, j] - pa[i]*pb[j]) / np.sqrt(pa[i]*pb[j])
V += res[i, j]**2
Up[i, j] = np.where(res[i, j] > 0, 1, 0)
Um[i, j] = np.where(Up[i, j] == 0, 1, 0)
V = np.sqrt(V / (min(a, b)-1))
# 戻り値:周辺確率(行)、周辺確率(列)、
# ピアソン残差、ピアソン残差が正、ピアソン残差が負、クラメルの連関係数
return pa, pb, res, Up, Um, V
## 算出処理
# 事後分布サンプリングデータから母比率pを取り出し
pis = idata1.posterior.p.stack(sample=('chain', 'draw')).data
# 算出結果を格納するリストの初期化
pas, pbs, ress, Ups, Ums, Vs, xastes = [], [], [], [], [], [], []
# 事後分布サンプリングデータ1件ごとに各統計量を繰り返し算出してリストに格納
for i in range(pis.shape[1]):
pa, pb, res, Up, Um, V = calc_stats2(pis[:, i])
pas.append(pa)
ress.append(res)
pbs.append(pb)
Ups.append(Up)
Ums.append(Um)
Vs.append(V)【実行結果】なし
■ クラメルの連関係数と周辺確率の事後分布
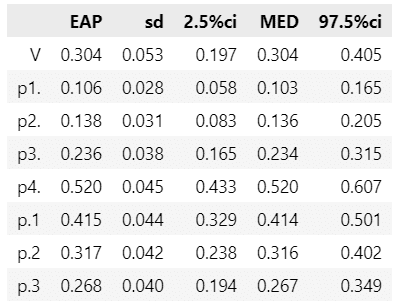
クラメルの連関係数と周辺確率の事後分布を表にまとめます。
テキストの表15.7に相当します。
### 問題(4)と問題(1)(2)のクラメルの連関係数と周辺確率の事後統計量の表示
# ※表15.7に相当
# クラメルの連関係数と周辺確率の事後統計量を算出してデータフレームに格納
stats_df14 = pd.DataFrame({'V': calc_stats1(np.array(Vs)),
'p1.': calc_stats1(np.array(pas)[:, 0]),
'p2.': calc_stats1(np.array(pas)[:, 1]),
'p3.': calc_stats1(np.array(pas)[:, 2]),
'p4.': calc_stats1(np.array(pas)[:, 3]),
'p.1': calc_stats1(np.array(pbs)[:, 0]),
'p.2': calc_stats1(np.array(pbs)[:, 1]),
'p.3': calc_stats1(np.array(pbs)[:, 2]),},
index=colname).T
# データフレームの表示
display(stats_df14.round(3))【実行結果】
テキストの結果とほぼ一致しています。
クラメルの連関係数$${V}$$は$${0.304}$$であり、クロス集計表全体の連関の程度は高くないでしょう。
問題(4)の誤答の比率は$${p_{4.}=0.520}$$であり、テキストは「誤答」が多いことが気になる、とコメントしています。
■ ピアソン残差
続いてピアソン残差を箱ひげ図で確認します。
テキストの図15.3に相当します。
### 問題(4)と問題(1)(2)のピアソン残差e_ijの描画 ※図15.3に相当
## 初期値設定
# x軸目盛ラベルの設定
tmp_names = [r'$e_{11}$正答・0点', r'$e_{12}$正答・1点', r'$e_{13}$正答・2点',
r'$e_{21}$公式・0点', r'$e_{22}$公式・1点', r'$e_{23}$公式・2点',
r'$e_{31}$圧差・0点', r'$e_{32}$圧差・1点', r'$e_{33}$圧差・2点',
r'$e_{41}$誤答・0点', r'$e_{42}$誤答・1点', r'$e_{43}$誤答・2点', ]
# ピアソン残差ressを問題(4)と問題(1)(2)の組み合わせごとに取り出してリスト化
# 箱ひげ図の描画用データに利用
tmp_list = [np.array(ress)[:, i, j] for i in range(a) for j in range(b)]
## 描画処理
# 描画領域の指定
plt.figure(figsize=(8, 4))
ax = plt.subplot()
# ピアソン残差の箱ひげ図の描画
ax.boxplot(x=tmp_list)
# y軸0の赤い水平点線の描画
ax.axhline(0, color='red', lw=0.5, ls='--')
# 修飾
ax.set_xticklabels(tmp_names, rotation=30)
ax.set(ylabel='ピアソン残差 $e_{ij}$', xlabel='問題(4)と問題(1)(2)の組み合わせ',
ylim=(-0.45, 0.61))
plt.show()【実行結果】
ピアソン残差が正のセルは独立な場合より高い比率で観察され、負のセルは独立な場合より低い比率で観察されるそうです。

【分析】~テキストにならって
テキストは$${e_{13}}$$の「問題(4)を正答」で「問題(1)(2)も正答」だけでなく、$${e_{33}}$$「問題(4)を上下水圧差」と答えた「問題(1)(2)も正答」も0超となっている点に着目して、「上下水圧差」と答えた学生にも物体が受ける浮力の大きさが体積に比例することを理解している人が一定数含まれていると考えられる、としています。
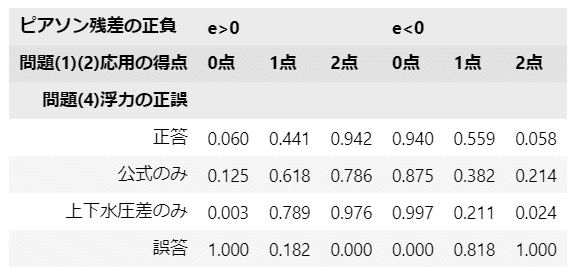
ピアソン残差が0超または0未満になる確率を表にまとめます。
テキストの表15.8に相当します。
### ピアソン残差がe_ij>0(左)、e_ij<0(右)の確率の算出 ※表15.8に相当
## マルチインデックスの設定
# 列
col_arrays = [['e>0']*3 + ['e<0']*3, ['0点','1点','2点']*2 ]
columns = pd.MultiIndex.from_arrays(
col_arrays, names=['ピアソン残差の正負', '問題(1)(2)応用の得点'])
# 行
idx_arrays = [['正答', '公式のみ', '上下水圧差のみ', '誤答']]
index = pd.MultiIndex.from_arrays(idx_arrays, names=['問題(4)浮力の正誤'])
## データフレーム化
# ピアソン残差の正・負データ(Ups,Ums)をデータフレーム化
stats_df15 = pd.DataFrame(np.hstack([np.array(Ups).mean(axis=0),
np.array(Ums).mean(axis=0)]),
columns=columns, index=index)
# データフレームの表示
display(stats_df15.round(3))【実行結果】
基本的な浮力の問題(4)が正答の場合、応用問題(1)(2)を正答する確率が$${0.942}$$です。
基本的な浮力の問題(4)が「上下水圧差」の場合は、応用問題(1)(2)を正答する確率が$${0.975}$$であり、(4)正答の場合よりも確率が高いです!
逆に、基本的な浮力の問題(4)が誤答の場合、応用問題(1)(2)を誤答する確率が$${1}$$です。
ふう、今回の分析は盛り沢山でしたね。
少々休憩しましょう。


モデル2:問題(4)と問題(3)
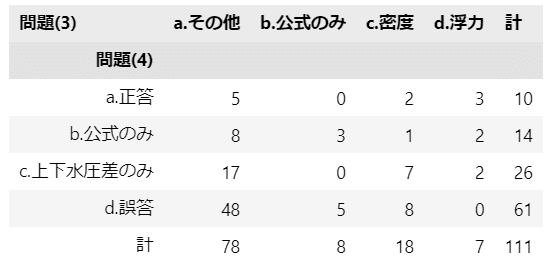
このモデルに投入するクロス集計表を作成します。
出力結果はテキストの表15.9に相当します。
### 問題(4)と問題(3)のクロス集計表の表示 ※表15.9に相当
# データ加工用に一時データフレームを作成
data_tmp = data.copy()
# 問題(4)の値に回答類型名を設定
subtitle3 = ['a.その他', 'b.公式のみ', 'c.密度', 'd.浮力']
data_tmp['q3'] = data_tmp['q3'].apply(lambda x: subtitle3[x])
subtitle4 = ['d.誤答', 'c.上下水圧差のみ', 'b.公式のみ', 'a.正答']
data_tmp['q4'] = data_tmp['q4'].apply(lambda x: subtitle4[x])
# 列名の変更
data_tmp.rename(columns={'q4': '問題(4)', 'q3': '問題(3)'}, inplace=True)
# 問題(4)と問題(1)(2)合計のピボットテーブルの作成
stats_df21 = data_tmp.pivot_table(
index='問題(4)', columns='問題(3)', values='id', aggfunc='count',
margins=True, margins_name='計', fill_value=0)
# ピボットテーブルの表示
display(stats_df21)【実行結果】
問題(3)の a.その他と b.公式のみが誤答、c.密度と d.浮力が正答です。
モデルの数式表現
目指したいPyMCのモデルの「なんちゃって数式」表記です。
大まかにはモデル1と変わっていません。
$${N2}$$はクロス集計表の総計 111 です。
ディリクレ分布の引数$${\text{a}}$$には$${4\times4=16}$$の1が並んでいます。
$$
\begin{align*}
p &\sim \text{Dirichlet}\ (\text{a}=(1,1,\cdots, 1)) \\
likelihood &\sim \text{Multinomial}\ (\text{n}=N2,\ \text{p}=p) \\
\end{align*}
$$
1.モデルの定義
数式表現を実直にモデル記述します。
xv_data2は観測値であり、クロス集計表の各セルを平坦化したものです。
また、テキストの Stan コードではモデル内でクラメルの連関係数やピアソン残差などを計算していますが、このモデルでは計算していません。
### モデルの定義
## データの準備
# 目的変数:問題(4)と問題(3)のクロス集計表を平坦化
xv_data2 = stats_df21.iloc[:4, :4].values.flatten()
# クロス集計表の合計
N2 = xv_data2.sum()
# 添字のリスト
suffix = [int(f'{i}{j}') for i in range(1, 5) for j in range(1, 5)]
## モデルの定義
with pm.Model() as model2:
## coordの定義
# データのインデックス
model2.add_coord('data', values=suffix, mutable=True)
## dataの定義
# 目的変数:クロス集計表の平坦化データ
x = pm.ConstantData('x', value=xv_data2, dims='data')
## 事前分布:確率合計1になるディリクレ分布
p = pm.Dirichlet('p', a=np.ones(len(xv_data2)), dims='data')
## 尤度:多項分布
likelihood = pm.Multinomial('likelihood', n=N2, p=p, observed=x,
dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の1つを設定しました。データの行の座標:名前「data」、値「行インデックス」
dataの定義
次の1つを設定しました。クロス集計表の各セル値:x (目的変数)
パラメータの事前分布
ディリクレ分布を用いて確率パラメータ$${p}$$の合計が1になるようにしています。
尤度
試行回数パラメータに回答者数、確率パラメータにクロス集計表の各セルの比率を持つ多項分布です。
2.モデルの外観の確認
### モデルの表示
model2【実行結果】
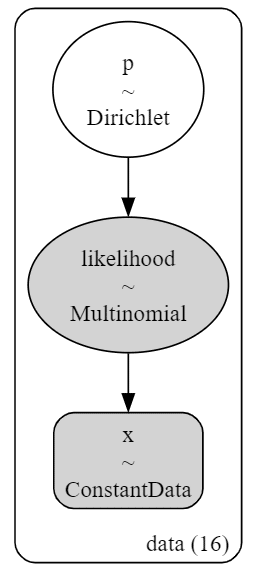
すごくシンプルです2!

### モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ10秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 10秒
# テキスト: iter=11000, warmup=1000, chains=5
with model2:
idata2 = pm.sample(draws=10000, tune=1000, chains=5, target_accept=0.8,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95, round_to=3)【実行結果】
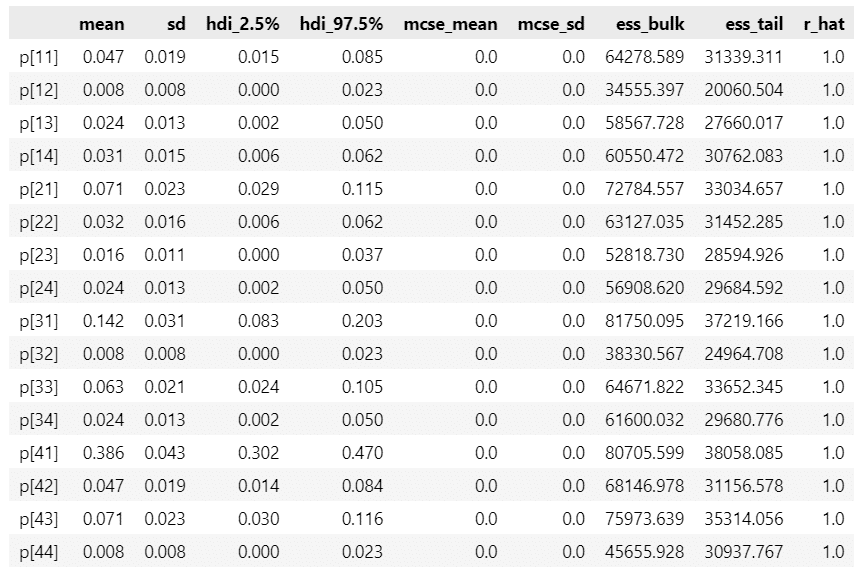
トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata2, compact=False)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.事後予測サンプリング
目的変数$${x}$$の事後予測からサンプリングします。
### 事後予測サンプリング
with model2:
idata2.extend(pm.sample_posterior_predictive(idata2, random_seed=1234))【実行結果】

事後予測プロットでモデルの予測を確認しましょう。
### 事後分布プロットの描画
pm.plot_ppc(idata2, num_pp_samples=100, random_seed=1234);【実行結果】
黒線の観測値とそこそこ近い?感触ということにしましょう。
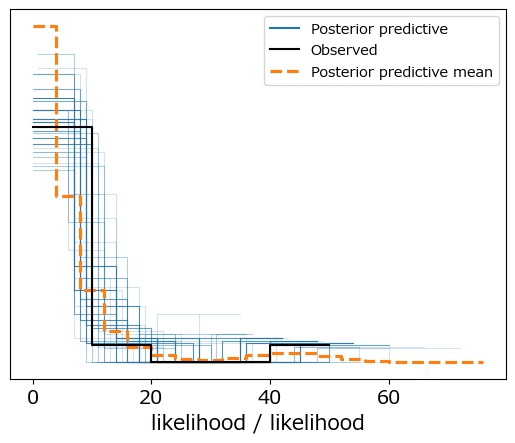
事後予測統計量を確認しましょう。
### 事後予測サンプリングの統計量の表示
pm.summary(idata2.posterior_predictive.likelihood, round_to=1)【実行結果】

6.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata1 をpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch15.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch15.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)
モデル2の分析
共通変数を作成します。
### 共通変数の定義
# 行数a、列数b
a, b, = 4, 4
ab = a * b■ クロス集計表の母比率の事後統計量
クロス集計表の母比率$${p}$$の要約統計量を算出します。
テキストの図15.10上段に相当します。
### 問題(4)と問題(3)のパラメータの事後分布の要約統計量の算出 ※表15.10上に相当
# 表示する変数名の一時リスト化 p11, p12, ・・・, p43, p44
tmp_names = [f'p{i+1}{j+1}' for i in range(a) for j in range(b)]
# 母比率pの事後分布サンプリングデータを取り出して一時変数に格納
tmp = idata2.posterior.p.stack(sample=('chain', 'draw')).data
# p(セルごと)に要約統計量算出を繰り返し処理して一時辞書に設定
tmp_dict = {}
for i in range(ab):
tmp_dict[tmp_names[i]] = calc_stats1(tmp[i])
# データフレーム化
stats_df22 = pd.DataFrame(tmp_dict, index=colname).T
# データフレームの表示
display(stats_df22.round(3))【実行結果】
テキストの結果とほぼ一致しています。
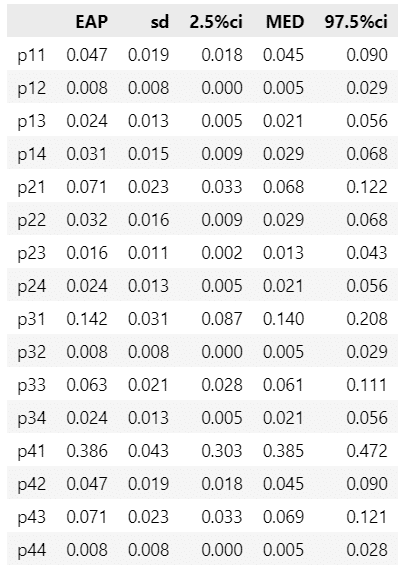
■ クロス集計表の値の事後予測統計量
続いてクロス集計表の値$${x}$$の要約統計量を算出します。
### 問題(4)と問題(3)のパラメータの事後分布の要約統計量の算出
# 表示する変数名の一時リスト化 x*11, x*12, ・・・, x*43, x*44
tmp_names = [f'x*{i+1}{j+1}' for i in range(a) for j in range(b)]
# 目的変数yの事後予測サンプリングデータを取り出し
tmp = idata2.posterior_predictive.likelihood.stack(sample=('chain', 'draw')).data
# x(セルごと)に要約統計量算出を繰り返し処理して一時辞書に設定
tmp_dict = {}
for i in range(ab):
tmp_dict[tmp_names[i]] = calc_stats1(tmp[i])
# データフレーム化
stats_df23 = pd.DataFrame(tmp_dict, index=colname).T
# データフレームの表示
display(stats_df23.round(1))【実行結果】
事後平均値(EAP)は表15.9のクロス集計表の値に近いです。
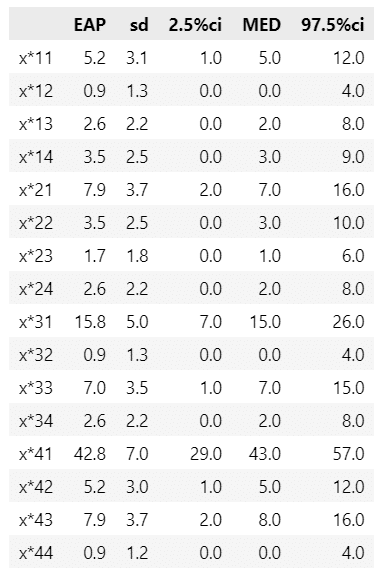
周辺確率、クラメルの連関係数、ピアソン残差を算出します。
### 問題(4)と問題(3)の周辺確率、ピアソン残差、クラメルの連関係数の算出
# 母比率pの事後分布サンプリングデータに基づいて上記統計量を計算します
## 算出処理
# 事後分布サンプリングデータから母比率pを取り出し
pis = idata2.posterior.p.stack(sample=('chain', 'draw')).data
# 算出結果を格納するリストの初期化
pas, pbs, ress, Ups, Ums, Vs, xastes = [], [], [], [], [], [], []
# 事後分布サンプリングデータ1件ごとに各統計量を繰り返し算出してリストに格納
for i in range(pis.shape[1]):
pa, pb, res, Up, Um, V = calc_stats2(pis[:, i])
pas.append(pa)
ress.append(res)
pbs.append(pb)
Ups.append(Up)
Ums.append(Um)
Vs.append(V)【実行結果】なし
■ クラメルの連関係数と周辺確率の事後分布
クラメルの連関係数と周辺確率の事後分布を表にまとめます。
テキストの表15.11に相当します。
### 問題(4)と問題(3)のクラメルの連関係数と周辺確率の事後統計量の表示
# ※表15.11に相当
# クラメルの連関係数と周辺確率の事後統計量を算出してデータフレームに格納
stats_df24 = pd.DataFrame({'V': calc_stats1(np.array(Vs)),
'p1.': calc_stats1(np.array(pas)[:, 0]),
'p2.': calc_stats1(np.array(pas)[:, 1]),
'p3.': calc_stats1(np.array(pas)[:, 2]),
'p4.': calc_stats1(np.array(pas)[:, 3]),
'p.1': calc_stats1(np.array(pbs)[:, 0]),
'p.2': calc_stats1(np.array(pbs)[:, 1]),
'p.3': calc_stats1(np.array(pbs)[:, 2]),
'p.4': calc_stats1(np.array(pbs)[:, 3]),},
index=colname).T
# データフレームの表示
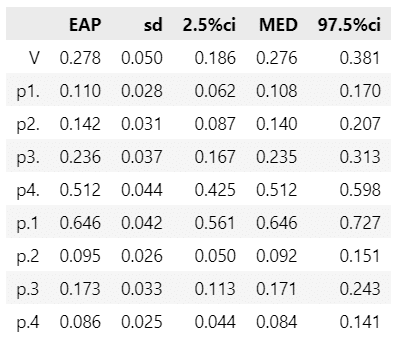
display(stats_df24.round(3))【実行結果】
テキストの結果とほぼ一致しています。
クラメルの連関係数$${V}$$は$${0.278}$$であり、クロス集計表全体の連関の程度は高くないでしょう。
問題(3)の誤答(公式も無し)の比率は$${p_{4.}=0.646}$$です。
■ ピアソン残差
続いてピアソン残差を箱ひげ図で確認します。
テキストの図15.4に相当します。
### 問題(4)と問題(3)のピアソン残差e_ijの描画 ※図15.4に相当
## 初期値設定
# x軸目盛ラベルの設定
tmp_names = [r'$e_{11}$正答・その他', r'$e_{12}$正答・公式', r'$e_{13}$正答・密度',
r'$e_{14}$正答・浮力',
r'$e_{21}$公式・その他', r'$e_{22}$公式・公式', r'$e_{23}$公式・密度',
r'$e_{24}$公式・浮力',
r'$e_{31}$圧差・その他', r'$e_{32}$圧差・公式', r'$e_{33}$圧差・密度',
r'$e_{34}$圧差・浮力',
r'$e_{41}$誤答・その他', r'$e_{42}$誤答・公式', r'$e_{43}$誤答・密度',
r'$e_{44}$誤答・浮力', ]
# ピアソン残差ressを問題(4)と問題(3)の組み合わせごとに取り出してリスト化
# 箱ひげ図の描画用データに利用
tmp_list = [np.array(ress)[:, i, j] for i in range(a) for j in range(b)]
## 描画処理
# 描画領域の指定
plt.figure(figsize=(10, 4))
ax = plt.subplot()
# ピアソン残差の箱ひげ図の描画
ax.boxplot(x=tmp_list)
# y軸0の赤い水平点線の描画
ax.axhline(0, color='red', lw=0.5, ls='--')
# 修飾
ax.set_xticklabels(tmp_names, rotation=30)
ax.set(ylabel='ピアソン残差 $e_{ij}$', xlabel='問題(4)と問題(1)(2)の組み合わせ',
ylim=(-0.45, 0.61))
plt.show()【実行結果】
ピアソン残差が正のセルは独立な場合より高い比率で観察され、負のセルは独立な場合より低い比率で観察されるそうです。

【分析】~テキストにならって
ピアソン残差が0を超えているセルに注目します。
$${e_{14}}$$「問題(4)が正答」「問題(3)の船が浮力で正答」より、浮力を理解している人は船が浮かぶ理由も正しく説明できている傾向があります。
一方で、$${e_{22}}$$「問題(4)が公式のみ」「問題(3)の船が公式のみで誤答」より、公式を暗記している人は船が浮かぶ理由を正確に説明できていない傾向があります。
また、「問題(4)が誤答」(浮力の理解が無い)人は$${e_{41}}$$「問題(3)の船が浮力も誤答(その他)」が正の領域にあり、かつ、$${e_{43}}$$「問題(3)密度」・$${e_{44}}$$「問題(3)浮力」が負の領域にある(この組み合わせは低い)ことから、浮力を理解していない人は浮力や密度で説明できていない傾向があります。
ピアソン残差が0超または0未満になる確率を表にまとめます。
テキストの表15.12に相当します。
### ピアソン残差がe_ij>0(左)、e_ij<0(右)の確率の算出 ※表15.12に相当
## マルチインデックスの設定
# 列
col_arrays = [['e>0']*4 + ['e<0']*4, ['その他','公式のみ','密度', '浮力']*2 ]
columns = pd.MultiIndex.from_arrays(
col_arrays, names=['ピアソン残差の正負', '問題(3)船の正誤'])
# 行
idx_arrays = [['正答', '公式のみ', '上下水圧差のみ', '誤答']]
index = pd.MultiIndex.from_arrays(idx_arrays, names=['問題(4)浮力の正誤'])
## データフレーム化
# ピアソン残差の正・負データ(Ups,Ums)をデータフレーム化
stats_df25 = pd.DataFrame(np.hstack([np.array(Ups).mean(axis=0),
np.array(Ums).mean(axis=0)]),
columns=columns, index=index)
# データフレームの表示
display(stats_df25.round(3))【実行結果】

【分析】~テキストにならって
基本的な浮力の問題(4)が正答の場合、船が浮かぶ理由を「浮力」で説明する確率が$${0.989}$$です。
基本的な浮力の問題(4)が「公式のみ」で、船が浮かぶ理由を「浮力」で説明する確率が$${0863}$$・「公式」で説明する確率が$${0.955}$$です。
このことから、公式を暗記する人は船が浮かぶ理由も公式を説明するだけにとどまる傾向があります。
■ 研究上の問いに関する確率
最後にテキスト167ページの3つの確率に取り組みます。
(式15.3) 浮力問題が正答 かつ 船が浮かぶ理由を浮力で説明する確率
(式15.4) 式15.3 × 浮力問題が誤答 かつ 船が浮かぶ理由を浮力で説明しない確率
(式15.5) 式15.4 × 浮力問題が上下水圧差 かつ 船が浮かぶ理由を密度で説明する確率
### テキスト167ページの同時確率 ※uexxはressから取り出せる
# 浮力問題が正答かつ船問題を浮力で説明する確率
# × 浮力問題が公式かつ船問題を公式で説明する確率
prob1 = ((np.array(ress)[:, 0, 3] > 0)*1 * (np.array(ress)[:, 1, 1] > 0)*1
).sum() / len(ress)
print(f'式15.3: {prob1:.3f}')
# prob1 × 浮力問題が誤答かつ船問題を浮力で説明しない確率
prob2 = prob1 * (np.array(ress)[:, 3, 3] < 0).sum() / len(ress)
print(f'式15.4: {prob2:.3f}')
# prob2 × 浮力問題が上下水圧差かつ船問題を密度で説明する確率
prob3 = prob2 * (np.array(Ups)[:, 2, 2] > 0).sum() / len(ress)
print(f'式15.5: {prob3:.3f}')【実行結果】
ほぼテキストの算出結果と一致しました。

1つ目と2つ目の確率はかなり高そうです。
・浮力問題が正答 かつ 船が浮かぶ理由を浮力で説明する
・浮力問題が誤答 かつ 船が浮かぶ理由を浮力で説明しない
は同時に成り立っていそうですね!
テキストのまとめに沿ってこの記事をまとめます。
浮力の意味を説明できる学生は応用問題や船が浮かぶ理由を適切に説明できる可能性が高い
以上で第15章は終了です。
おわりに
浮かぶ
実はこの原稿を書いている間、頭がぼんやりとして、奇妙な浮遊感に包まれていました。
昨日から微熱が続いているのです。
ぼーっとしながら書いた原稿はきっと、後日に大幅書き直しが発生するでしょう。
それでもいいのです。
体調の良し悪しは確率的な要素が混じっているでしょうし、だったら、ベイズモデルでいい方向に収束させてしまえばいいのです。
おわり
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
