
時系列分析入門【第6章 後編】関数データ解析・関数主成分分析をPythonで実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第6章「多変量時系列データの要約」のRスクリプトをお借りして、Python で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは「関数データ解析」と「関数主成分分析」です!
初めての分析手法であり、とても面白そうだ!と感じて、Pythonのパッケージを探すのが楽しかったです。
(注)テキストの手法の7割程度は私にとって「初物」でした。
しかし、またまた難易度の高いトピック。
今回は・・・、どうでしょう???
さあ、時系列分析を楽しんでいきましょう!
ちなみにこの記事がシリーズ最終回です。
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第6章 多変量時系列データの要約
この記事は「6.4 関数主成分分析」を実践いたします。
インポート
この章で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# WEBアクセス
import requests
# Rデータ読み取り
import rdata
# Rデータセット・動的因子分析
import statsmodels.api as sm
# 非負値行列因子分解
from sklearn.decomposition import NMF
# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')
関数データ解析というジャンル
テキストによると、関数データ解析は時系列データ$${\{ x(t_i):i=1, \cdots, N\}}$$を時刻を変数とする関数$${f(t)}$$とし、この関数の係数に対して統計解析を行う方法、とのこと。基本的な流れを次のように紹介しています。
時系列データを「基底関数」と呼ばれる関数の和で表現する。
時系列データを基底関数に展開できたら、「係数に対して」クラスタ分析や重回帰分析などの多変量解析を実行する。
1点目の基底関数をテキストに沿って確認していきましょう。
フーリエ級数(三角関数の和)とB-スプライン関数に取り組みます。
① データの読み込み
Rのfdaパッケージに含まれるデータセット「gait.knee」を読み込みます。
39人の歩行中の膝関節角度の変化を20時点記録したデータセットです。

大変です!警報発令です!ウーウー!
データセットがRスクリプトに埋め込まれています!

沈思黙考・・・

そうだ、Python 上で R を動かそう💡
pyper パッケージの登場です!

ただし、この方法が成立する前提条件として、利用環境に R がインストールされている必要があります。
R がインストールされていない場合には次善の策として、Google Colaboratory で R を動かして、データ取得する方法があります。
次のリンク記事の「苦肉の策」の部分に、Google Colaboratory で Rコード を動かす例を記載しておりますので、参考になさって下さい。

では、pyper を用いたデータ取得に進みましょう!
### インストール
pip install pyper### インポート
import pyperデータをダウンロードします。
### Rスクリプトファイルのダウンロード
# 設定:ダウンロードファイルの格納先パス+ファイル名
filename = r'./gait.R'
# ダウンロードの実行
url = r'https://www.psych.mcgill.ca/misc/fda/downloads/FDAfuns/R/data/' \
'gait.R'
res = requests.get(url)
with open(filename, mode='wb') as f:
f.write(res.content)【実行結果】なし
続いて R スクリプトを実行して、csvファイルを保存します。
### gait.Rを実行してgait.Knee Angleデータを取得する
# Rオブジェクトの作成
r = pyper.R()
# gait.Rを読みこんで実行
r('source("C:/心理学のための時系列分析入門/gait.R")')
# gait.Knee Angleデータをcsvファイルに出力
r('write.csv(gait[,,2], file="gait.csv", row.names=T)')【実行結果】省略
最後にCSVファイルを pandas のデータフレームに読み込みます。
### データの読み込み
gait_df = pd.read_csv('./gait.csv', index_col=0)
display(gait_df)【実行結果】
インデックスが時点、列のboy1~39が39人の歩行中の膝関節角度の変化データです。

② データの描画
39の時系列データの折れ線グラフを pandas の plot で描画します。
テキストの図6.7上に相当します。
### 元データのプロット ※図6.7上段に相当
gait_df.plot(lw=0.6, ls='--',
figsize=(8, 3), legend=False, xlabel='Time', ylabel='angle');【実行結果】
大まかには、全データの線の傾向が類似しているように見えます。


続いて関数データ解析の「基底関数」を調べましょう。
scikit-fda パッケージを利用します。
機械学習パッケージ scikit-learn のお友達みたいですね。
③ scikit-fda パッケージのインストール
必要に応じてインストールしてください。
### インストール
## scikit-fda
# anaconda
conda install -c conda-forge scikit-fda
# pip
pip install scikit-fdaインストールの際、「Microsoft Visual C++」を求められることがあります。
また、既に「Microsoft Visual C++」がインストール済みであっても、次のようなエラーが発生して、scikit-fda のインストールができない事態が発生することがあります。
【エラーメッセージ(例)】
not modified: 'build\_DP.c'
generating build_DP.c
(already up-to-date)
Compiling src/optimum_reparamN2.pyx because it changed.
[1/1] Cythonizing src/optimum_reparamN2.pyx
error: Microsoft Visual C++ 14.0 or greater is required. Get it with "Microsoft C++ Build Tools": https://visualstudio.microsoft.com/visual-cpp-build-tools/
次のサイトが「Microsoft Visual C++」対応の参考になります!
ありがとうございます!
④ インポート
無事に scikit-fda をインストールできましたら、インポートしましょう。
### インポート
import skfda
from skfda.representation.basis import FourierBasis, BSplineBasis
from skfda.preprocessing.dim_reduction import FPCA
from skfda.exploratory.visualization import FPCAPlot
⑤ データの変換
pandas のデータフレームを scikit-fda のデータ形式「FDataGrid」に変換します。
### pandasのDataFrameをFDataGridデータ形式にインポート
# 変換パラメータの設定 ※行:標本軸・列:時間軸
data_matrix = gait_df.T # データセット全体
grid_points = gait_df.T.columns.astype(float) # 時間軸の時点情報
# FDataGridデータにインポート
fd = skfda.FDataGrid(data_matrix=data_matrix, grid_points=grid_points)変換したデータを描画してみましょう。
scikit-fda の plot を利用します。
先ほどのテキスト図6.7上と同じ図になるはずです。
### 描画 by scikit-fda ※図6.7上段に相当
fig = plt.figure(figsize=(8, 3))
fd.plot(lw=0.6, ls='--', legend=False, fig=fig)
plt.xlabel('Time')
plt.ylabel('angle')
plt.show()【実行結果】
同じ図になりました!

⑥ フーリエ級数:基底関数の作成と当てはめ
いよいよ関数データ解析の「基底関数」の検討に入ります。
まず、フーリエ級数の基底関数を作成します。
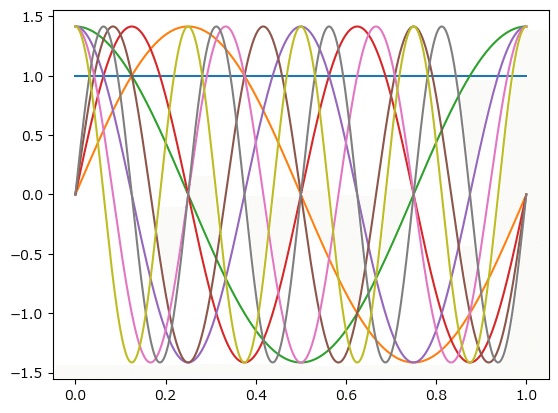
scikit-fda の FourierBasis() で8つの基底関数を組み合わせます。
引数 n_basis=8 で基底関数の数を指定します。
## フーリエ基底関数の作成
# https://fda.readthedocs.io/en/latest/auto_tutorial/plot_basis_representation.html
basis_ft = FourierBasis(n_basis=8)
print(type(basis_ft))
# 描画 by scikit.fda
basis_ft.plot()
plt.show()【実行結果】
basis_ft はフーリエ基底関数のクラスです。

sin・cosの三角関数の波が8つあります。
続いて、データセットに基底関数を当てはめます。
「basis_fd_ft = fd.to_basis(basis_ft)」が当てはめの実行部です。
### フーリエ基底関数の当てはめ
basis_fd_ft = fd.to_basis(basis_ft)
print(type(basis_fd_ft))【実行結果】
basis_fd_ft はFDataBasisクラスであることが分かりました。
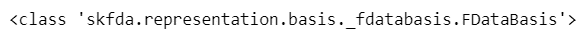
当てはめ後の近似曲線を描画します。
テキストの図6.7中に相当します。
# 描画 ※図6.7中段に相当
fig = plt.figure(figsize=(8, 3))
basis_fd_ft.plot(lw=0.6, ls='--', legend=False, fig=fig)
basis_fd_ft.mean().plot(lw=2, color='black', fig=fig)
plt.xlabel('Time')
plt.ylabel('angle')
plt.show()【実行結果】
黒線がフーリエ級数による平均関数です。
なかなかの適合具合です。
複数の関数を組み合わせてデータを表現するって、面白い発想ですね!


⑦ B-スプライン関数:基底関数の作成と当てはめ
続いて、B-スプライン関数の基底関数を作成します。
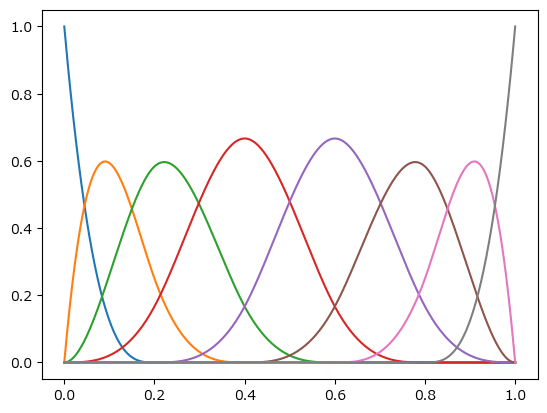
scikit-fda の BSplineBasis() で8つの基底関数を組み合わせます。
引数 n_basis=8 で基底関数の数を指定します。
また、 order=4 は3次のスプラインを指します。
### 基底関数の作成(B-スプライン関数)
## B-スプライン基底関数の作成
# https://fda.readthedocs.io/en/latest/auto_tutorial/plot_basis_representation.html
# 基底関数の数:8、スプラインのオーダー:4=3次
basis_bs = BSplineBasis(n_basis=8, order=4)
# 描画 by scikit.fda
basis_bs.plot()
plt.show()【実行結果】
8つの峰が左から右へ移動するような感じです。
続いて、データセットに基底関数を当てはめます。
### B-スプライン基底関数の当てはめ
basis_fd_bs = fd.to_basis(basis_bs)【実行結果】なし
当てはめ後の近似曲線を描画します。
テキストの図6.7下に相当します。
# 描画 ※図6.7下段に相当 ★テキストと異なる感じがする
fig = plt.figure(figsize=(8, 3))
basis_fd_bs.plot(lw=0.6, ls='--', legend=False, fig=fig)
basis_fd_bs.mean().plot(lw=2, color='black', fig=fig)
plt.xlabel('Time')
plt.ylabel('angle')
plt.show()【実行結果】
黒線がB-スプライン関数による平均関数です。
テキストでは右端に跳ね上がりがありますが、この図では跳ね上がりがほとんどありません。テキストの結果と若干異なる感じです。

2つの基底関数を比べて描画してみましょう。
### 2つの基底関数の当てはめデータの平均値を可視化して比較
fig = plt.figure(figsize=(8, 3))
basis_fd_ft.mean().plot(color='tab:blue', fig=fig, label='フーリエ級数')
basis_fd_bs.mean().plot(color='tomato', fig=fig, label='B-スプライン関数:3次')
plt.legend();【実行結果】
B-スプライン関数のほうが滑らかな曲線になっています。


関数主成分分析(FPCA)
先ほどのフーリエ級数で関数化したデータに対して関数主成分分析による次元削減を実施します。
関数主成分分析も scikit-fda を活用します。
FCPA を利用します。
① 関数主成分分析の実行
基底関数の8を主成分にする(n_components=8)FCPAオブジェクトを生成して、fitメソッドでフーリエ級数で関数化したデータを与えて、FCPAを実行します。
### 関数主成分分析の実行
## 基底関数と同じ数の主成分の算出
# FCPAオブジェクトの生成
fpca = FPCA(n_components=8)
# FCPAの実行 対象データ:フーリエ級数で関数化したデータ
fpca.fit(basis_fd_ft)
print(type(fpca))【実行結果】
fpca は FCPA のクラスです。
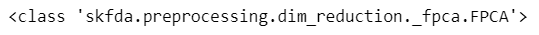
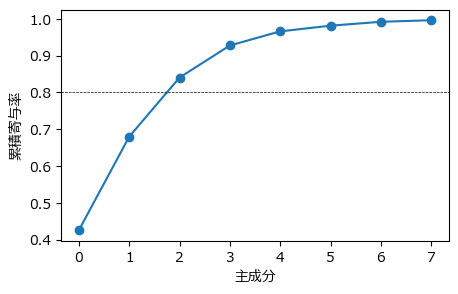
② 累計寄与率の描画
累計寄与率を描画して分析対象の主成分の数を検討します。
テキストの図6.8左に相当します。
### 寄与率の描画
plt.figure(figsize=(5, 3))
plt.plot(fpca.explained_variance_ratio_.cumsum(), '-o')
plt.axhline(0.8, color='black', lw=0.5, ls='--')
plt.xlabel('主成分')
plt.ylabel('累積寄与率')
plt.show()【実行結果】
テキスト通り、第3主成分までで累計寄与率が80%を超えました。
③ 主成分の固有関数の描画
第3主成分までの固有関数を描画します。
テキストの図6.8右に相当します。
### 第3主成分までの主成分関数の描画 ※図6.8右に相当
# ★テキストと比べてPC1が正負逆転している
# ※components_は固有ベクトルを関数化した固有関数と思われる
# 主成分関数の描画 by scikit-fda
fpca.components_[:3].plot(fig=plt.figure(figsize=(4, 4)))
# 修飾
plt.axhline(0, color='black', lw=0.5, ls='--')
plt.xlabel('Time')
plt.ylabel('Values')
plt.legend(['PC1', 'PC2', 'PC3'], bbox_to_anchor=(1, 1))
plt.show()【実行結果】
テキストと比べて、PC1:第1主成分が正負逆転している感じがします。
PC2:第2主成分とPC3:第3主成分はテキストと類似している感じです。
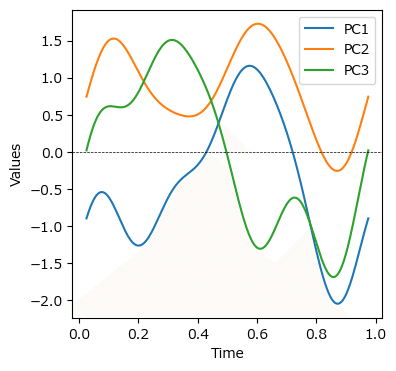
分析結果はテキストのとおりになると思われます。
・第1主成分は0.2と0.9付近の角度の大きさ(凹部分)と関係
・第2主成分は膝を大きく曲げたとき(0.6付近)の角度の大きさと関係
④ 第1~3主成分得点の描画
テキストの図6.9に相当します。
テキストは第1~3主成分得点が$${\pm 1 SD}$$のときの関節の角度変化の特徴を見るプロットです。
この記事では、FPCAPlot() を利用して、係数の2倍のレンジのときの特徴の図になります。
### FPCAプロットの描画 ※図6.9に相当
# ★レンジ:テキストは標準偏差、こちらは係数の倍数
FPCAPlot(
mean=basis_fd_ft.mean()[:3], # 平均関数:FDataオブジェクト
components=fpca.components_[:3], # 主成分関数:FDataオブジェクト
factor=2, # 加算・減算される主成分関数の倍数
fig=plt.figure(figsize=(10, 4)), # figureの指定
n_rows=1, # 描画行数の指定
# n_cols=3, # 描画列数の指定
).plot()
plt.legend(['平均', f'加減算:倍数2', f'加減算:倍数2'], bbox_to_anchor=(1, 1))
plt.tight_layout()【実行結果】
ざっくりとテキストに類似している感じがいたします(細かいことは抜きにして)。

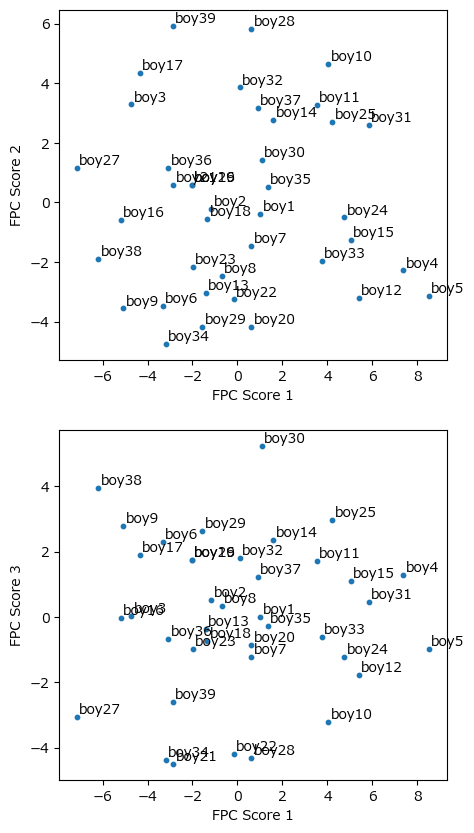
⑤ 各参加者の関数主成分得点の描画
テキストの図6.10に相当します。
③のプロットで分かった通り、第1主成分の正負がテキストと逆転しているので、この⑤のプロットも逆転しています。
### 主成分得点のプロット ※図6.10に相当 ★テキストと比べてPC1の正負が逆転している
# 主成分得点の算出
score = gait_pca.transform(gait_ft)
# 主成分得点の描画
fig, ax = plt.subplots(2, 1, figsize=(5, 10))
for i in range(2):
# 主成分得点の散布図の描画
ax[i].scatter(score[:, 0], score[:, i+1], s=10)
# 参加者の注釈を設定
for j, text in enumerate(gait_df.columns):
ax[i].annotate(text, xy=(score[j, 0]+0.1, score[j, i+1]+0.1))
# 修飾
ax[i].set(xlabel=f'FPC Score {1}', ylabel=f'FPC Score {i+2}')【実行結果】
x軸:第1主成分がテキストと左右逆転していますが、特徴は同じだと思われます。
関数主成分分析による次元削減はうまく行ったと思います!やったね!
8つの関数でデータを表現して、その後に、データの成分を3つに減らして表現し直す、こんなデータ分析でした。
以上で終了です。
お疲れ様でした。

最後に
今回は最終回です。
素晴らしい時系列分析体験の機会をくださった、テキストの著者の先生、誠にありがとうございました。
そして、長期に渡ってお付き合いいただき、ブログを読んでくださって、ありがとうございました。
次の記事

前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
