
チームアップとか数学とか~その2~
チームアップとか数学とか~その1~の続きです。
その2では縦型ではなく、水平ネットワーク型の構造に関してお話しようと思います。
■水平ネットワーク型コミュニケーション構造
前回の記事では縦型ツリー構造のコミュニケーション図を載っけてみました。では「教師ー学生」の一方通行な枠組みが解体された時の組織の構造を挙げてみようと思います。これは僕が哲学の授業で実際に体験した感じです。
今回もnは人、pはコミュニケーションパスの数を表します。

・その1
これはツリーと変わりません。たった1人だとまぁどこでも一緒ですね。

・その2
これもツリーと変わりませんね。2人でも一緒です。
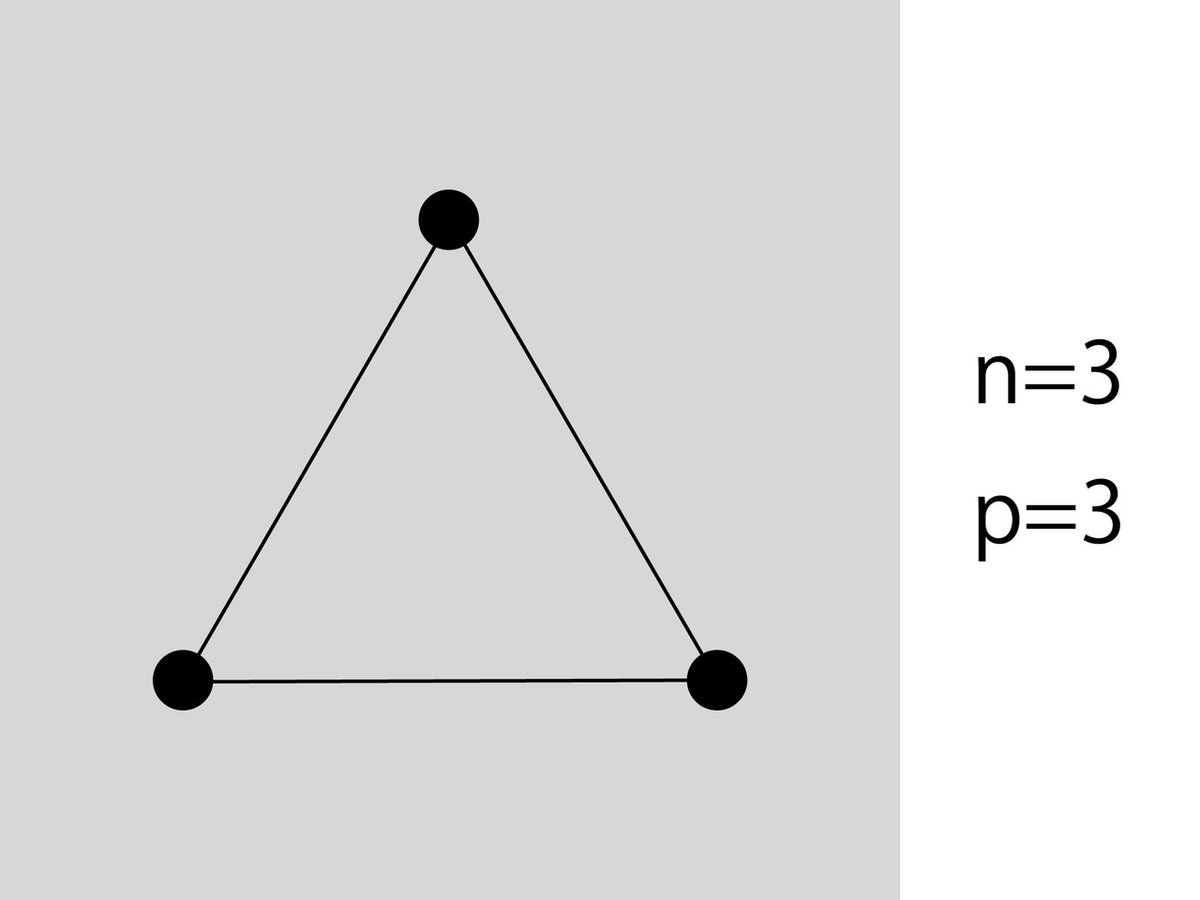
・その3
ここからツリーと変わってきます。ツリーに比べてパスが一つ増えました。
ではここから一気にその6まで並べてみましょう。
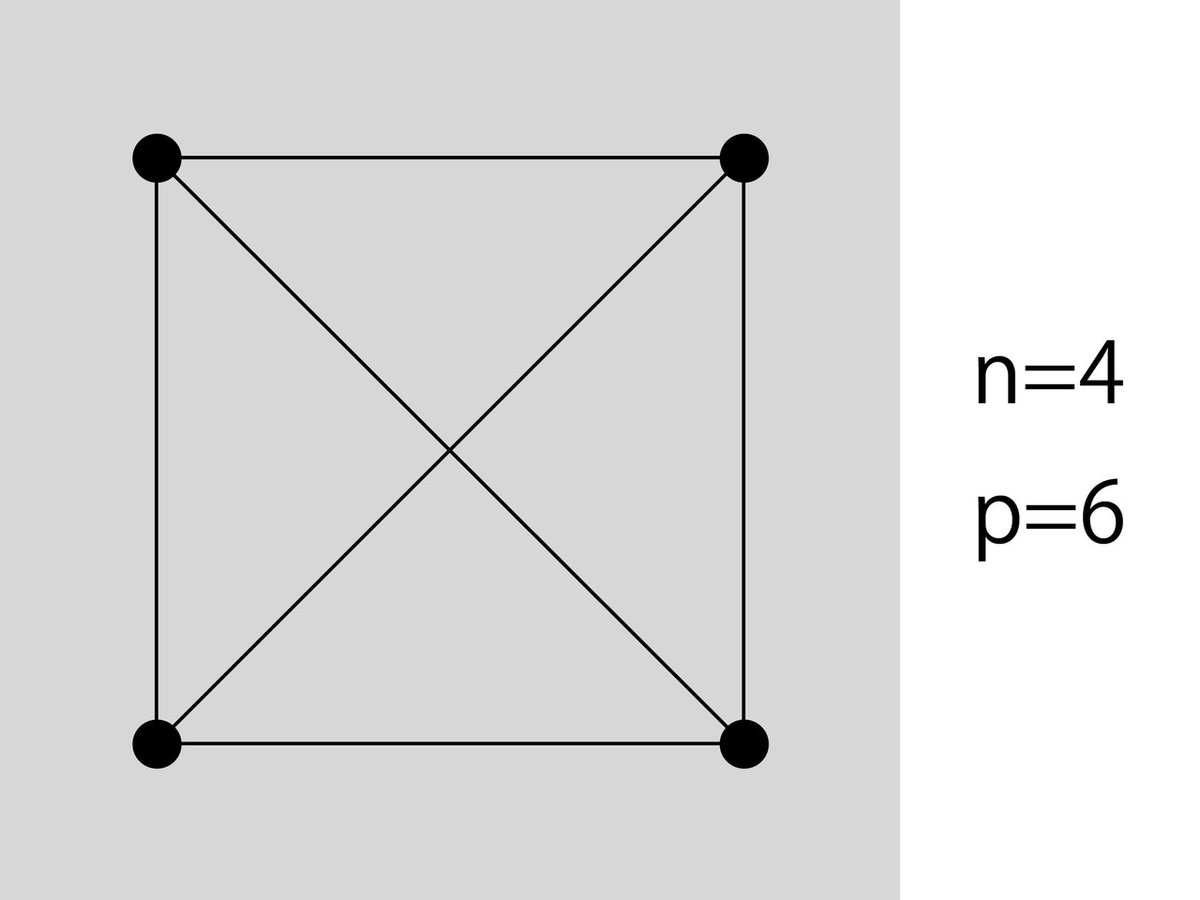


おおすげぇ!ツリーに比べて格段にパス数が増えてる!
表にすると以下のようになります

お、なんか複雑・・・。ん?待てよ

おお!なんか法則あるぞ!(この時の僕はまさかpだけ見てれば良いとは思っていませんでした。アホアホです)
ちょっと複雑なので、一般化は次の項で
■一般化

とりあえず数式としてはこんな感じの漸化式になりました。これどうやって計算したら良いんだっけ?たしかシグマとかにしたはず・・・

表とにらめっこしてたら、こうなってたことに気が付きました。上の漸化式の「n」に当たる部分は「a」の部分だったわけですが、これよくよく考えたらあんまいらなかったみたいです。では計算してみましょう。

以上で一般化完了です。
■んで?コイツはなんなんさ?
で、これなんですが、注目すべきは縦型ツリー構造に対してすごい勢いでコミュニケーションパスの数が増えていることです。
「n=6」の時なんか「p=5対15」ですよ
これだけコミュニケーションの可能性が広がるとすると。組織全体を行き来する情報量が一気に増え出力が格段に上がります。成員各々が各々の教師としてお互いを教育するような空間ができるわけですね。
ただし、やり取りされる情報量やそのためのパスが増えるということは、それらをコントロールしたり、まとめたりするスキルやキャパシティも同じ倍率で増えると考えられます。
つまり、ファシリテーション能力やリーダーシップが取れていないと、空中分解や分断のリスクが跳ね上がります。必然的に成員全員が情報をやり取りするため、意見の食い違いの可能性も高まります。
その2はこんなところで、最後のまとめにその3を書こうと思います。
サポートいただけると励みになります!
