
深層学習で洋服の写真を並び替え(メトリックラーニングアプローチ)|札幌の長期インターンシップインタビュー
私たちダイアモンドヘッド株式会社ではファッションアパレルに特化した商品情報を管理する自社サービスを展開しています。
サービスの中では商品に紐づく写真を多数管理しており、写真は規則に則って順序付け(並び替え)された状態でショッピングモールやショッピングアプリへと写真を含めたデータが配信されてます。
今回の記事は、商品画像の並び順を深層学習を用いて自動化する実験を主に長期インターンシップ参加者と新卒入社数名で取り組んだレポートを記事化しました。
関連レポート
参加したインターンシッププログラム
以下、レポート本文です。
1. 背景
現状では、弊社運営のスタジオで撮影した画像をお客様が閲覧できるようになった後、ECサイトにおいて表示したい画像の並びになるよう人手で並び替えを行っている。
しかし、全商品の全画像を手動で並び替えるのは非常にコストが大きい。
2. 目的
「1. 背景」で述べた画像の並び替えを、近年注目を浴びている人工知能技術である「深層学習」を活用して、自動で高速に行うことを試みる。
「レギュレーションに基づく画像ソート」(以下、本タスク)とは、与えられた画像群内の画像を任意のレギュレーションに基づいて並びかえる(ソート)することである。
例えば、以下のようなレギュレーションのもとで入力となる画像群が与えられたとすると、その画像群内の画像を、「バック」が写っている画像は最初に、「洗濯タグ」が写っている画像は最後に、「袖」が写っている画像は中盤に、というように並び替えることを言う。

3. アプローチ
3-1. 回帰アプローチ
本タスクへのランキング問題としての私のアプローチについて概要を述べる。(分類問題としてのアプローチは別記事を参照。)
画像が入力として与えられた際に、その画像が所望のソートされた画像順列内でどの位置に存在するかを機械学習モデルに予測させたいと考えた。
よって、所望の画像順列の最初を0、最後を1としたときに、画像順列内においてどの程度の位置にあるのかを、入力画像に対してスカラー値を出力させることによって予測させることとした。
例えば、以下のような例であれば、「バック」が写っている画像は「0」を、「裾」が写っている画像は「0.375」を、「ブランドタグ」が写っている画像に対しては「0.875」をそれぞれ出力させたい。
以降、このTargetとなる値のことを “Percentile Rank” と呼ぶこととする。画像群内の全画像に対してこの ”Percentile Rank” を予測させ、その予測値を昇順にソートすることによって、ソートされた画像順列を得る。

つまり、機械学習モデルに対しては、以下のように、画像を入力としてその画像に対する “Percentile Rank” を出力させる。

この機械学習モデルを構築する手法として、近年、自然言語処理や画像認識の分野で注目されている深層学習を用いる。
3-1-1. アーキテクチャ
実験におけるアーキテクチャは以下のようにした。

事前学習済みモデルにSwim Transformer V2[4]を使ったのは、前回の実験である程度性能がよく、学習が早く終わることが分かったためである。
そして、同時にメインカラーとサブカラーを並び替えするため、2次元の特徴量 f' を追加しました。それが「画像内のアイテムがその商品のメインカラーか否か」と「各商品に登録されている画像枚数」です。
全体の流れは、入力画像 x が swin transformer v2 $${\phi}$$(・) に入力し、特徴$${ f}$$ を取り出します。そして、画像特徴$${ f}$$ と追加特徴 $${ f' }$$ を結合させ、全結合層 F に入力し、最終的にPercentile rank $${\hat{y}}$$を出力します。
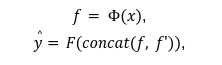
その中、$${concat(A,B)}$$はAとBを結合する関数です。
3-1-2. トレーニング
回帰アプローチでは、回帰問題で一般的に使用される L1 Loss $${Lce}$$を利用して学習を行っております。
L1 loss
L1損失は、予測値 $${\hat{y}}$$ と実際の値(ターゲット) $${y}$$ との差の絶対値の合計を計算する方法です。この損失を最小化することで予測したPercentile Rankは理想のPercentile Rankとより近くなります。
具体的には、L1損失は次のように定義されます:
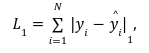
その中Nは全部のサンプル数、$${|・|_1}$$ は絶対値を意味します。
3-1-3. 推論
推論では、アプローチで書いたように、入力が画像で出力がPercentile Rankとなっております。最終的にPercentile Rankによって画像の並び替えを行います。
3-2. 分類アプローチ
以前取り組んだランキング問題としてのアプローチ、すなわち、PointWise的な「Percentile Rank」を用いたアプローチとPairwise的なアプローチでは、新たなレギュレーションに基づいた画像ソートが必要になったときに、そのレギュレーションに則った教師データの作成が必要であることを指摘いただき、そのようなコストを削減するために画像分類によるアプローチを考えた。
これは、1枚の画像に対して、画像に「裾」が写っているのか「袖」が写っているのかなどを機械に予測させ、そのラベルに基づいて単純な辞書のソートなどで画像の並びを得ようとするものである。つまり、画像を分類し、その分類クラスを用いてソートする。
この分類問題としてのアプローチのメリットとデメリットをまとめると以下のようになる。
メリット
画像のクラスに基づいてソートするため、レギュレーションごとに学習させる必要がなくなる。
各画像につき一度しか深層学習モデルに入力しないため、計算量が画像枚数に対して線形。(pairwise手法では$${O(N^2):N}$$は画像枚数)
デメリット
クラス分類の性能がそのままソートの性能に直結する。(回帰より、モデルの出力値がソート結果に大きく影響する。)
ディープランニングの方法として、大量なラベル付きの訓練データが必要です。未来可能なカテゴリー横展開や、違うクライアントで利用する際は、高いラベリングコストが想像できます。
結論から述べると、商品及びモデルの画像に対する分類は以下のような結果になった。
結果
商品画像とモデル画像の全17クラス分類でもある程度の性能は発揮できる。
裾や袖の間違いが多い。
学習データに含まれていないような珍しいカットや撮影方法の画像は間違えやすい。→幅広いジャンルと撮影スタイルのデータで学習することが最も重要に思える。
3-2-1. アーキテクチャ
実験におけるアーキテクチャは以下のようにした。事前学習済みモデルにConvNeXt[3]を使ったのは、前回の実験である程度性能がよく、学習が早く終わることが分かったためである。
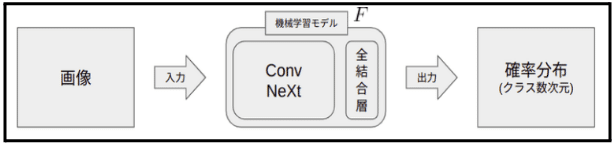
全体の流れは、入力画像 $${x}$$をモデル $${F(・)}$$に入力し、各クラスの確率分布 $${\hat{y}}$$ を出力します。式は以下です:
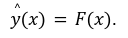
3-2-2. トレーニング
分類アプローチでは、分類問題で一般的に使用される CrossEntropy Loss $${Lce}$$を利用して学習を行っております。
CrossEntropy Loss
CrossEntropy Lossは、分類タスクの性能を評価するためによく使われる損失関数の一つです。この損失関数は、デルが予測するクラス $${\hat{y}}$$と実際のクラス $${y}$$との違いを数値化し、モデルの訓練中に最小化しようとする損失関数です。この損失を最小化することで、モデルは正確な分類を行うように学習します。式は以下です:

その中Nは全部のサンプル数、Mは全部のクラス数です。
3-2-3. 推論
推論では、アプローチで書いたように、入力が画像で出力が各クラスの確率分布となっております。最終的に各クラスの確率分布の中で確率が一番高いクラスを分類結果として見ます。その分類結果によって画像の並び替えを行います。
3-3. メトリックラーニング
以前の分類問題アプローチでは、ConvNeXtを用いた直接的な分類手法が採用されていました。この手法は、大量の訓練データが必要であり、現在では各クラスに対して千枚の画像を使用することで良好な結果を得ています。ただし、将来的にクラスの数が増加すると、ラベリングのコストが膨大になる可能性があるため、新しいアプローチを模索しました。
そのため、今回はメトリックラーニング(Metric Learning)のアプローチを採用しました。メトリックラーニングは、データポイント間の距離や類似性を学習し、その情報を活用してクラス分類、クラスタリング、異常検出などのタスクを実行します。
これは、少量のデータで効果的に学習できる機械学習のアプローチの一つです。メトリックラーニングは、データポイント間の相対的な距離や類似性に焦点を当てるため、少量のデータでも効果的な学習が可能です。少数のデータポイントから距離や類似性のパターンを抽出し、モデルの性能向上に寄与します。
このメトリックラーニングのメリットとデメリットをまとめると以下のようになる。
メリット
よりカテゴリーを横展開しやすい。少量なデータしかない状況でも、学習することが可能となりました。
所要な訓練時間が減ります。訓練の際は少量なデータで学習を行うため、大量データと比べ所要な訓練時間が減ってます。
デメリット
効果はどうしても大量訓練データで学習するモデルより悪いです。クラス分類の性能がソートの性能に直結するため、最終のソートの性能に負の影響を与える可能性があります。
結論から述べると、商品及びモデルの画像に対する分類は以下のような結果になった。
結果
各クラスでのサンプルが10枚のみの状況でもある程度の性能は発揮できます。
3-3-1. アーキテクチャ

実験におけるアーキテクチャは上の図に示します。事前学習済みのConvNeXt$${\phi}$$ を使って画像 $${x}$$ をembedding空間に投影し、特徴 $${f}$$と転換します。そして、この特徴を全結合層 $${F}$$ に入力し、確率分布 $${\hat{y}}$$ を出力します。式は以下となります:

3-3-2. トレーニング
今回のアプローチでは、主に分類問題において一般的に使用される CrossEntropy Loss $${Lce}$$と、メトリックラーニングに広く採用されている Triplet Loss $${L_{tri}}$$ が利用されています。それぞれの説明は以下となります。
CrossEntropy Loss
CrossEntropy Lossは、分類タスクの性能を評価するためによく使われる損失関数の一つです。この損失関数は、デルが予測するクラス $${\hat{y}}$$と実際のクラス $${y}$$との違いを数値化し、モデルの訓練中に最小化しようとする損失関数です。この損失を最小化することで、モデルは正確な分類を行うように学習します。式は以下です:
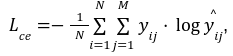
その中Nは全部のサンプル数、Mは全部のクラス数です。
Triplet Loss [2]
Triplet Lossは、類似性を評価するために使用され、3つのサンプル(トリプレット)から構成されます:
Anchor(アンカー): 類似性を評価したいオブジェクトや画像のサンプル。
Positive(ポジティブ): Anchorと類似しているサンプル。同じクラスまたは同じカテゴリに属するもの。
Negative(ネガティブ): Anchorと異なるサンプル。異なるクラスまたは異なるカテゴリに属するもの。
Triplet Lossの目標は下の図で示した様に、AnchorとPositiveの間の距離をできるだけ縮め、同時にAnchorとNegativeの間の距離をできるだけ広げることです。
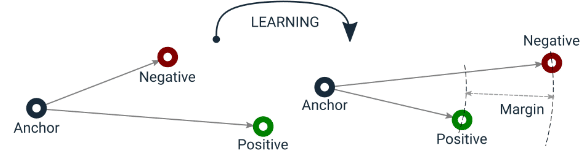
具体的に今回の流れは下の図の様です。まずはデータ・セットから目標のanchor $${x}$$ とそれに対応するpositive sample $${x^+}$$ や、negative sample $${x^-}$$ をランダムで選び、重み共有のモデル(ConvNeXt)で特徴を取り出します。
Anchorや、positive sample、negative sampleの特徴はそれぞれ $${f}$$、$${f^+}$$、$${f^-}$$ と表します。これによってtriplet lossを計算します。
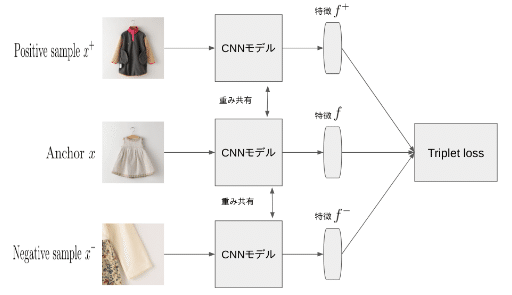
Triplet lossの式は以下です:
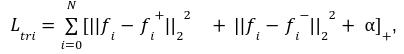
その中、$${|{|・||_2}^2}$$ は Euclidean distance (ユークリッド距離)の2乗を表し、 は余分な margin (マージン、しきい値)を示します、$${[・]_+}$$は正の部分を抽出する事を示します。
Overall Loss
以上のlossを加えてモデルの訓練を行っております。式は以下です:

その中$${\lambda_{ce}}$$,$${\lambda_{tri}}$$は各lossをバランスさせるための重みです。デフォルトでは全部1と設定されてます。
3-3-3. 推論
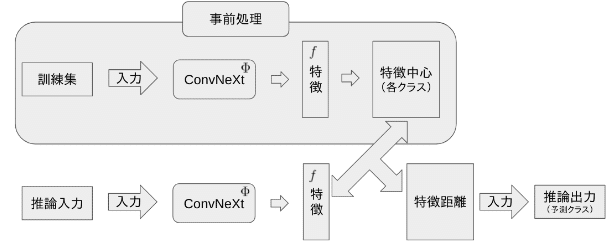
推論を行う前に、事前処理として、訓練集中の各クラスの特徴中心を計算します。そして、推論では、入力画像の特徴を取り出し、計算済みの各クラスの特徴中心と距離を計算し、距離が一番近いクラスを最終の分類結果とします。そして、その分類結果によって画像の並び替えを行います。
4. 実験
実験は主に3つの部分と別れて掲載します:
メインカラーとサブカラーのTopsに対して、回帰アプローチの効果。
Topsで計17クラスに対し、分類アプローチの効果。
少量の訓練データで学習を行う条件に対し、一般的な分類アプローチとメトリックラーニングの分類アプローチの効果差。
4-1. [回帰アプローチ] メインカラーとサブカラーのTops
本実験では、サブカラーも含むTシャツ・Yシャツに対して、以下のようなレギュレーションでの画像ソートを試みた。

レギュレーションを見るとわかるように、実験サブカラーを含めたレギュレーションにした。
ただし、サブカラー内の順番(例えば、サブカラーに赤と青があるとき、どちらをさきにならべるか)は定義しておらず、無秩序になっている。
また、全部で 20 epochの学習を行った。Trainの損失は以下のようになった。最適化のステップを重ねるごとに徐々に損失が下がっており、学習が進んでいることが確認できた。
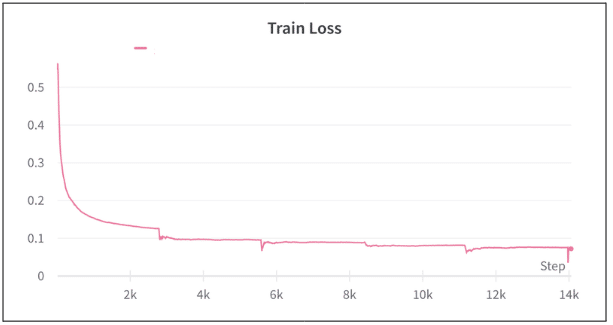
検証ロスは以下のようになった。
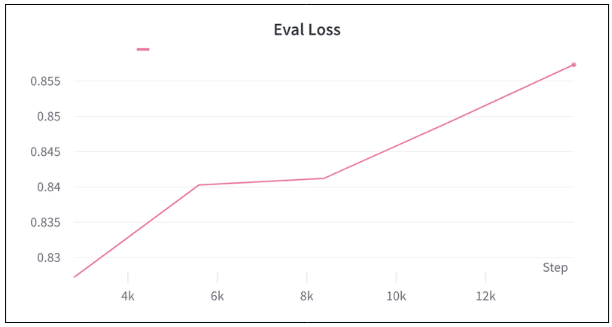
考察:評価に用いた412品番中 204品番 で正解データとモデルの予測が完全に一致。残りの208品番では、どこかしら間違っている。
原因は、画像にうつっているものがメインカラーの画像か否かをうまく認識できていないからであると予測される。例を以下に示す。


商品の形状に引っ張られすぎており、メインカラーか否かを追加した特徴量のみでは識別できない。一方で正解しているものは以下のようなもので簡単なものが多かった。


単色カラー内での並び替えを目的としたPercentileRankを予測する回帰を、複数カラー内での並び替えに特徴量を追加して無理やり適用したが、結果はあまり良くなかった。
複数カラー内での並び替えには、それに適したモデルを開発するほうが適切であると思われる。
4-2. [分類アプローチ] Topsで計17クラスの画像入れ替え
本実験ではレギュレーションに基づく画像ソートの分類問題としてのアプローチの最終目標として、モデルが写った画像と服の画像を同時に分類するモデルの作成を試みた。ここで定義したクラスは以下の17クラスである。
1_brand_tag (ブランドタグ)
2_material (生地感)
3_print (プリント)
4_wash_tag (お洗濯タグなどのタグ類)
5_sleeve (袖)
6_sleeve_hem (袖&裾)
7_hem (裾)
8_feature (特徴カット)
9_collar (襟)
10_back (後ろからなど全体像を撮ったもの)
11_far_back (モデルの全身&後ろ向き)
12_far_front (モデルの全身&前)
13_far_side (モデルの全身&横)
14_near_back (モデルのより&後ろ)
15_near_front (モデルのより&前)
16_near_side (モデルのより&横)
17_near_zoom (モデルの一部分ズーム)
各クラスの例を次ページ以降に挙げる。



上記のクラスのラベル付けを行い学習を行った。Trianの損失は以下のようになった。

Validの損失は以下のようになった。
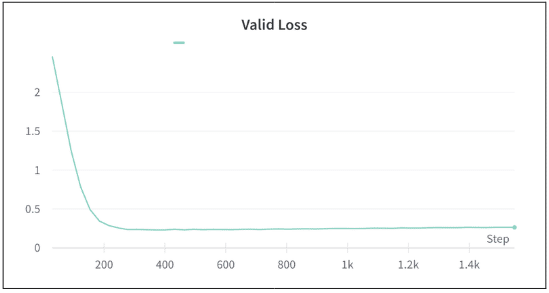
次に、学習に使用した汎用的なカテゴリとは別のカテゴリ5つに対して推論を行い検証した。以下がその検証結果である。
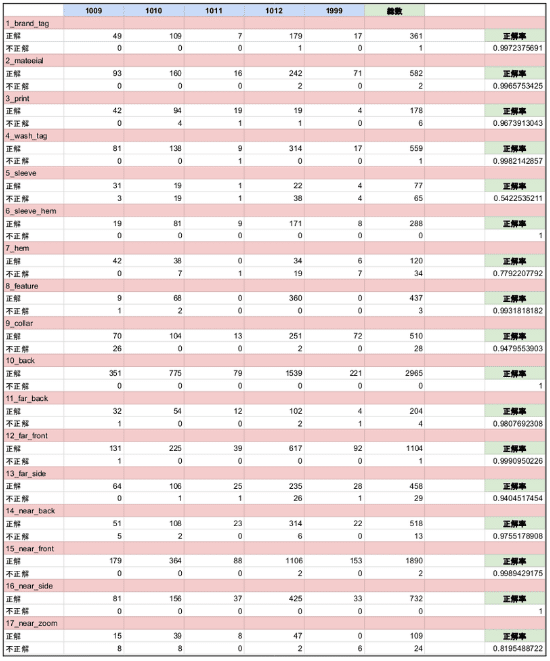
袖と裾の性能が著しく悪く、17_near_zoomもその次に悪い。一方で、それ以外のクラスではある程度の性能は出ている。
次に間違えたものの例を記載する。
1_brand_tag :
ブランドタグについて、唯一の間違いは以下であった。

これは、1_brand_tagとしたのは理解できるが、9_collar として欲しいところなので、間違いとなっている。
2_material:
間違った2つは以下であった。

ポケットを左のように写したような画像は訓練データにほとんどない。
右は人が着ているので17_near_zoomとしているが、この判定はかなり難しいように思える。
3_print:
間違えた6件は以下のようなものであった。

左上は人判定できていない。右上の間違いは、文字列に反応しているように思える。洗濯タグは間違えたくない。
4_wash_tag:

brand_tagとのミスが予想されていたが、予想通りになった。
5_sleeve:

基本的に学習データにあまり含まれていない画像で間違える。肘パッチやパーカー等の前開きの服を裏返したような画像は少なかった。
左下は裾も写っているので不正解としているが、sleeveともとれなくないし、featureともとれなくない。
6_sleeve_hem:
間違いはなかった。
7_hem :

5_sleeveでも述べたように、前開きの服の裏地を撮ったものは少ない為間違えたと考えられる。
左下以外は裾が写っておりhemとしても間違いではないかと思う。左下のように袖を裾と判別するのは避けたい。
8_feature :

真ん中や右はfeatureと考えられるような考えられないような。
9_collar :

上記のようなベストが間違いの全てであった。ベストは学習データにほとんど含まれていない。
11_far_back:

数枚の間違いがある。基本的にはfar_frontと間違える。
12_far_front:

farとnearの判定を間違えている。
13_far_side:

far内で間違える。原因は不明。
14_near_back:

マネキンに服を着せて撮影された画像は学習データにほとんど含まれていないため、間違えたように思える。おそらくマネキンを人と判定している。
15_near_front:

マネキンに服を着せて撮影された画像は学習データにほとんど含まれていない。
17_near_zoom:

マネキン画像とベストは学習にあまり含まれていない。右上と左下はあまり間違えたくない。
4-3. [メトリックラーニング] 少量の訓練データで学習を行う
人物なしで、一定の資料量を持つ計9つのクラスの中からサンプルを選び、深層学習の訓練を行います。嘗て栗田さんは各クラスで100枚から200枚くらい利用して訓練するのと違って、今回は少量データで訓練することを検討してます。少量データでの訓練を目指すため、各クラスからそれぞれ10枚を選んで訓練セットとします。
また、検証セットでは50枚のサンプルを選び、残りのサンプルはすべてテストセットとして使用します。[100枚から200枚=>10枚]
以下に利用するクラスを示します:

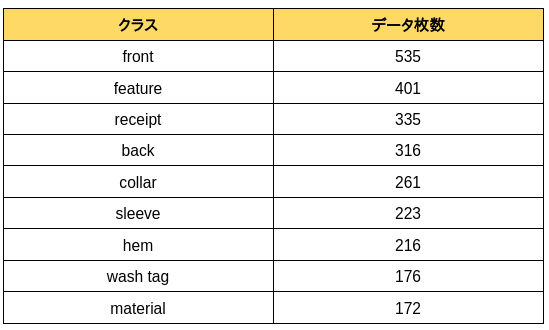
標準分類アプローチ
ここでまず試した方法は標準のCNN分類です。やり方は「3-2. 分類アプローチ」と同じく、ただ各クラスのサンプル数を本来の100〜200枚から10枚に変更するのみです。
TrianとValidの損失は以下のようになった。
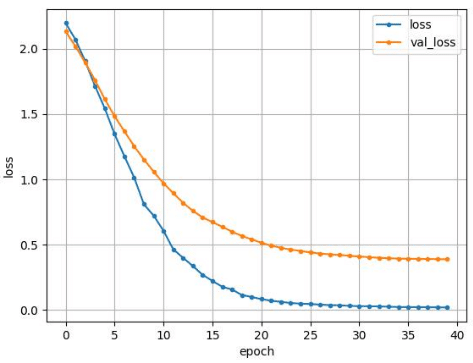
上記のグラフから、overfittingを起こしていないことが分かります。
訓練の結果は以下となります
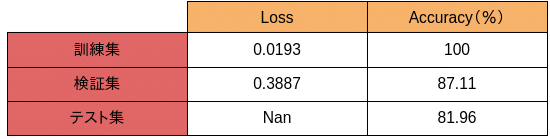
検証集や、テスト集での精度は基本80以上出しています。
各クラスのテスト精度は以下となります。wash tagとreceiptは完璧に分類しています。だが、feature、back、frontの精度が相対的に低いです。
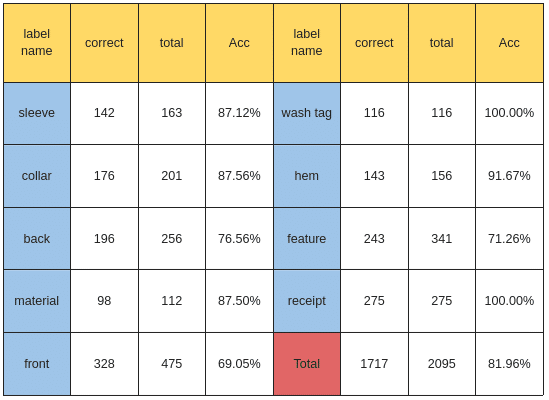
多かった間違い
服の正面と背面は同じく間違えやすい傾向が存在しています。
そして、特徴(feature)の中にポケットや、ボタン、紐など違う要素が存在しているので、よく素材(material)や、袖(sleeve)と間違います。
メトリックラーニング(CrossEntropy+Triplet loss)
メトリックラーニングは標準分類方法と違って、分類器を訓練して分類するのではなく、画像を同じクラスは近い、違うクラスは遠いの特徴空間を投影し、その空間で特徴距離を計算することで分類を行います。
TrianとValidの損失は以下のようになった。
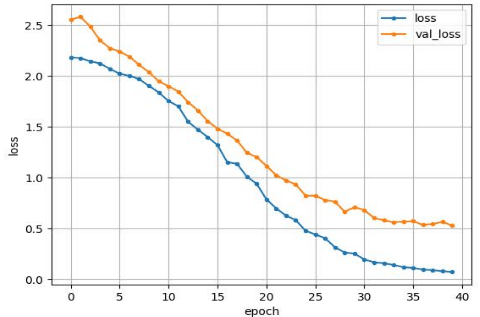
上記のグラフから、overfittingを起こしていないことが分かります。
訓練の結果は以下となります
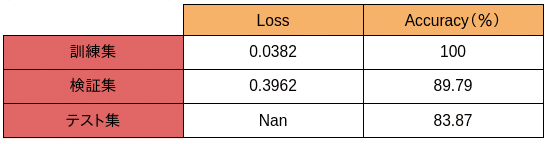
検証集や、テスト集での精度は基本80以上出しています。そして、標準分類方法と比べると少し効果が上がってます。
標準分類方法とメトリックラーニング(CrossEntropy+Triplet loss)の訓練集、検証集、およびテスト集における精度を比較した結果を以下に示します。メトリックラーニングは標準分類方法と同様に分類器を使用するため、分類器を利用した精度と特徴距離に基づく分類の精度も比較します。
分類器を利用した精度は「metric(分類器)」と表示し、特徴距離に基づく分類の精度は「metric(距離)」と表示します。
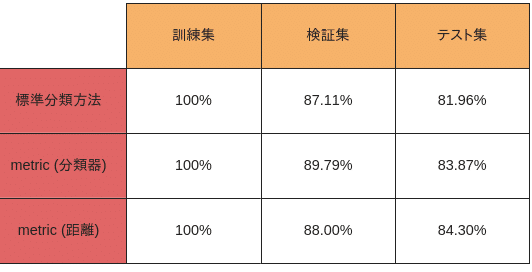
各クラスのテスト精度は以下となります。wash tagとreceiptは完璧に分類しています。feature、backの精度は上がりましたが、collarとfrontの精度は下がっております。
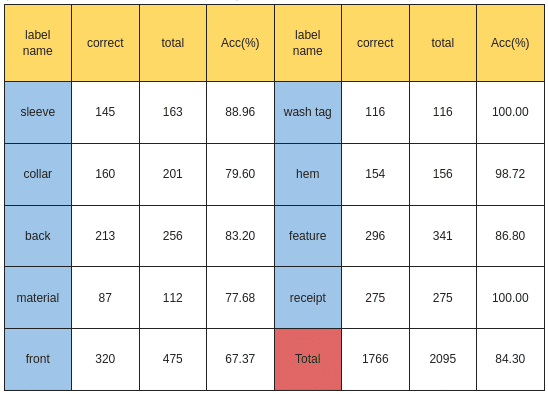
多かった間違い
服の正面と背面は同じく間違えやすい傾向が存在しています。
collarはsleeveや、featureなどと間違えやすいです。
5. これまでのまとめ[総評]:
9クラスそして、各クラス10枚で訓練したとしても、一定分類能力を持つモデルを訓練することが可能ということが分かりました。
服の正面や背面の間違いが多い
これからの課題
違うカテゴリーや、クライアントでモデルの学習効果を試します。
Reference
[1] Y. Wen, K. Zhang, Z. Li, and Y. Qiao, ‘A Discriminative Feature Learning Approach for Deep Face Recognition’, in Computer Vision – ECCV 2016, B. Leibe, J. Matas, N. Sebe, and M. Welling, Eds., in Lecture Notes in Computer Science. Cham: Springer International Publishing, 2016, pp. 499–515. doi: 10.1007/978-3-319-46478-7_31.
[2] E. Hoffer and N. Ailon, ‘Deep Metric Learning Using Triplet Network’, in Similarity-Based Pattern Recognition, A. Feragen, M. Pelillo, and M. Loog, Eds., in Lecture Notes in Computer Science. Cham: Springer International Publishing, 2015, pp. 84–92. doi: 10.1007/978-3-319-24261-3_7.
[3] Z. Liu, H. Mao, C.-Y. Wu, C. Feichtenhofer, T. Darrell, and S. Xie, ‘A ConvNet for the 2020s’. arXiv, Mar. 02, 2022. doi: 10.48550/arXiv.2201.03545.
[4] Z. Liu et al., ‘Swin Transformer V2: Scaling Up Capacity and Resolution’. arXiv, Apr. 11, 2022. doi: 10.48550/arXiv.2111.09883.
Appendix.
Appendix 1. Triplet loss の Positive sample と Negative sample 選び方
Positive sample と Negative sampleの選び方に対して、一番簡単なやり方はランダムでanchor と同じクラスのサンプルを positive sample とみなし、anchor と違うクラスのサンプルを negative sampleとみなします。しかし、より良い効果を求めるため、今回はhardest pairを利用しました。
Hardest pair(最も難しいペア)を利用する理由は、モデルの訓練効率を向上させ、学習プロセスを安定化させるためです。最も難しいペアは、Triplet の中で、anchorサンプルとnegativeサンプルとの距離が最も近いものを指します。それ以外にhardest positive pairも利用しています、即ち、anchorサンプルとpositiveサンプルとの距離が最も遠いものを選びます。この選び方によって、より効果的な特徴の学習と訓練プロセスの安定化が期待できます。
Appendix 2. Center Loss [1]
Center Lossは、Triplet Lossと同様に、類似性を評価するための損失関数の一つですが、Triplet lossとは異なり、サンプル間のトリプレットを使用せず、代わりに各クラスごとにサンプルの中心(クラス固有の特徴的な表現)を学習します。
Center Lossの主なアイデアは下の図の様に、各クラスごとにそのクラスの中心(centroid)を定義し、ネットワークがこれらの中心にサンプルを近づけるように学習することです。
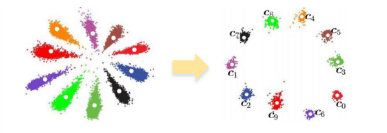
具体的なやり方としては、先ず各クラスの中心点 c を下の式で計算します。

その中、もし $${\delta}$$(条件) の条件達成したら $${\delta}$$(条件)=1、達成しないなら $${\delta}$$(条件)=0。
そして、各クラスの中心点を計算した後、中心点とサンプル特徴の距離を計算することでサンプルをよりクラス中心に近づけるように学習します。Center loss $${L_{center}}$$の式は以下となります。
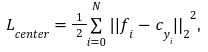
その中、 $${|{|・||_2}^2}$$は Euclidean distance (ユークリッド距離)の2乗を表します。
インターンシップに興味をお持ちの方へ
募集要項や応募選考フローや良くある質問などの情報を長期インターンシップ募集サイトにまとめました。興味をお持ちの方はリンク先をご確認下さいますようお願いします。

