統計検定準1級ワークブックの解説(第7章の本文例題,章末問題)
統計検定準1級ワークブックのマガジン
自己紹介
QC検定1級, 統計検定2級を持っています。現在は統計検定準1級の合格を目指しています。まずは統計準1級ワークブックを進めています。そこで自分なりの解答を共有していこうと考えています。※解答のみで問題は載せません。
所感
極限定理と漸近理論の章です。中心極限定理について詳しく書かれていました。Xnが独立に正規分布N(μ, σ²)に従うと仮定する。このとき
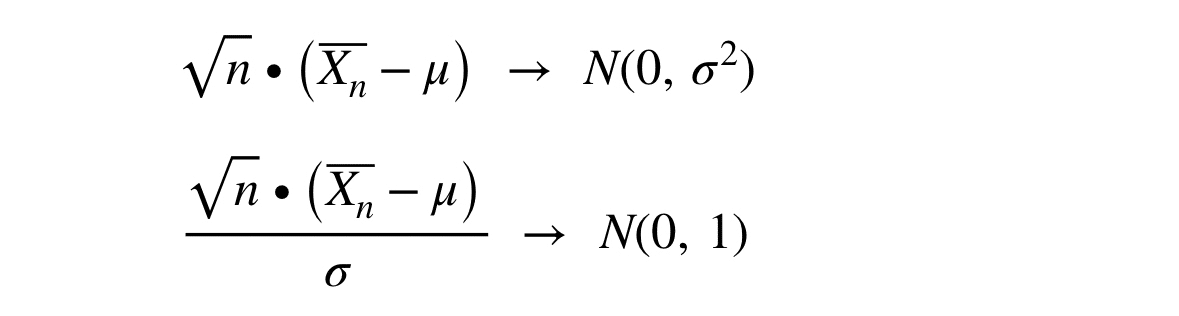
正規分布に収束する。上の2つの式は同じ内容です。本文中では上の式が使われてます。しかし個人的に下の式の方が分かりやすいです。収束先も標準正規分布になります。自分の分かりやすい解釈で覚えていきたいです。他にはデルタ法が初見でしたが便利そうです。
本文例題の解説
例7.1
求めるのはZnがどのような値に収束するかである。問題文より

例7.2
求めるのはXnがどのような分布に収束するかである。まずΦは標準正規分布の累積分布関数で

例7.3
理解できなかったため省略。
例7.4
求めるのは分布の収束先。f(x)=x²としてデルタ法を使う。このとき

例7.5
求めるのは分布の収束先。問題文よりXnとYnが標準正規分布に収束する。連続写像定理よりXn²+Yn²は自由度2のχ²分布に分布が収束する。
章末問題の解説
問7.1
求めるのは確率の近似値。k回目に数字の3が現れる確率変数Xkはベルヌーイ分布に従う。

したがって、期待値=1/6, 分散=1/6•5/6=5/36。求める確率は

の形に式変形する。このとき右辺は正規分布N(0, 1)に収束する。式の形としては、正規分布N(1/6, 5/36)を標準化している。

問7.2(1)
求めるのは

がどのような分布に収束するかである。これは中心極限定理そのものである。したがって正規分布N(0, 1)に収束する。
(2)

f(x)=x³としてデルタ法を考える。f(x)が連続微分可能なのでテイラー展開より

(3)
求めるのは

がどのような分布に収束するかである。2乗の中身は(1)よりN(0, 1)に収束する。その2乗なので、自由度1のχ²分布に収束する。
問題文が掲載されている書籍
Amazonのアソシエイトとして、このアカウントは適格販売により収入を得ています。
