
Pythonを用いた住宅ローンシミュレーション(金利上昇時の想定前編)
こんにちは。分析屋のFと申します。
前回の「Pythonを用いた住宅ローンシミュレーション(繰上げ返済後編)」に続き、住宅ローンについて今回は金利上昇を想定するという内容でお伝えしていきます。
前回の記事はこちらになります。
住宅ローンは金利タイプには大きく変動金利と固定金利に分類できます。変動金利は短期プライムレートに連動して、返済期間中は随時変動するものとなっております。固定金利は長期プライムレートに連動しますが、契約時の金利が完済まで適用されます。住宅ローンの金利タイプをどちらにすべきかお悩みの方、既に変動金利を契約中の方で金利上昇に不安を感じている方が多いと思いましたので金利上昇時のシミュレーションによって、総返済額、総利息への影響をお伝えできればと思います。今回のシミュレーションでは実際にとある銀行が発表している2023年11月時点の金利を使用致します。その他の基本情報は前回と変わらず返済期間420ヶ月(35年)、借入額4000万と致します。
本記事の構成は以下の通りとなります。
1.金利上昇の概要
変動金利では毎年4月と10月に金利が改定されますが金利が上昇しても毎月の返済額への影響がすぐに出るのかと言うとそうではございません。「5年ルール」と「125%ルール」がそれぞれ存在しているからです。(金融機関によっては適用していない処もございます。)
5年ルールとは金利が上昇しても5年間は毎月の返済額が変わらないというルールになります。
125%ルールとは金利が上昇した際に(5年ルールを経た上での)返済額は現在の返済額の125%が上限となります。
いずれのルールも金利上昇時の毎月の返済額の急上昇を防ぐための利用者にとってはありがたいルールに思えますが、注意が必要です。5年ルールの適用は5年間は毎月の返済額が変わらないと述べましたが、毎月の返済額に占める元金の割合が小さくなりますため返済スピードが遅くなります。更に5年経過後は毎月の返済額も増えるため、その結果として総返済額は増えることになります。
今回は変動金利を選択した場合に金利上昇開始時期をユーザーの入力により指定し、金利上昇幅を0.05%刻みに総返済額を算出致します。例えば契約時の変動金利が0.3%として金利上昇開始時期が8年目、金利上昇幅が0.1%ならば以下のような金利推移になります。(実際にこのような右肩上がりの金利推移は考えられないですが。)
1年目〜7年目は0.3%
8年目〜12年目は0.4%
13年目〜17年目は0.5%
18年目〜22年目は0.6%
23年目〜27年目は0.7%
28年目〜32年目は0.8%
33年目〜35年目は0.9%
プログラムで出力する内容の一つ目として、変動金利が全く上昇しなかった場合と比較して総返済額の差を出力致します。二つ目としては固定金利の総返済額と比較して損益分岐点を導出するプログラムを作成致しました。
今回のプログラムは5年ルールは考慮いたしますが、125%ルールは考慮しておりません。(125%ルールの考慮が必要な金利上昇はあまり現実的と考えておりません。)
2.金利上昇時のプログラムの仕様
2-1. 償還表
基本情報に加えて、変動金利の場合の金利(%)、固定金利の場合の金利(%)、金利上昇開始時期をユーザーにて入力頂く必要がございます。これに加えてfixfl(固定フラグ)を引数で指定して固定金利/変動金利の指定により、後続の「総返済額の比較表」にて比較できるように致しました。
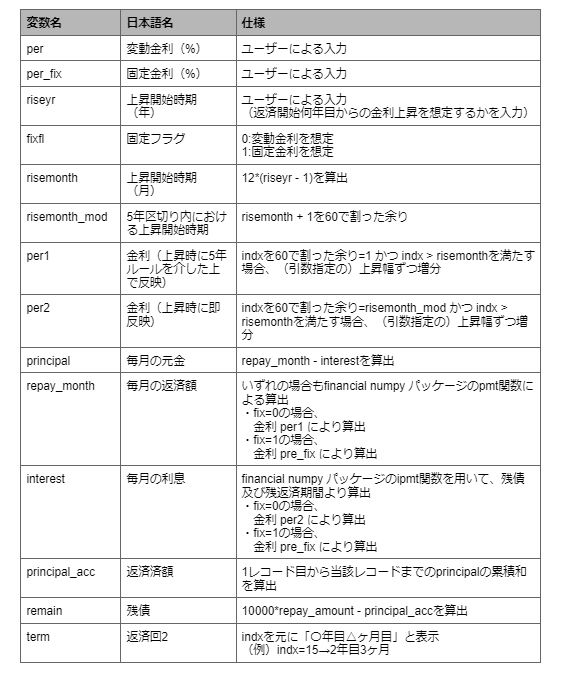
2-2. 総返済額の比較表
2-1.で作成した償還表作成時のユーザーによる入力情報及びfixfl(固定フラグ)を用いて各種比較を行います。本表の「変動勝利」「固定勝利」への切替わるper_fluを出力することで損益分岐点が分かります。

3.金利上昇時のプログラム及び実行結果
今回は実際にとある銀行が2023年11月に発表している内容(変動金利0.375%、固定金利1.93%)にて金利上昇開始時期を5年目と15年目それぞれにてプログラムを実行致します。
<プログラム>
import numpy as np
import numpy_financial as npf
import pandas as pd
import math
##############################
#### 基本情報(元利均等返済) ####
##############################
# 金利
per = 0.375
per_fix = 1.93
# 返済期間
period = 12*35
# 借入額
repay_amount = 4000
########################
#### 金利上昇開始時期 ####
########################
riseyr = 5
# 空のデータフレーム
kihon = pd.DataFrame()
# 関数定義
def create_term(x):
if x % 12 == 0:
y = str(math.ceil(x/12))+'年目12ヶ月目'
else:
y = str(math.ceil(x/12))+'年目'+str(x%12)+'ヶ月目'
return y
def get_lag(x, y, z):
if x != 1:
w = y + z
return w
# 償還表作成
def rise(riseyr_ , width_ , fixfl):
# 毎月の返済額
repay_month = math.floor(npf.pmt(0.01*per/12, period, -repay_amount*10000))
risemonth = 12 * (riseyr_ - 1)
risemonth_mod = np.mod(risemonth + 1, 60)
per1 = per
per2 = per
# 返済済
principal_acc = 0
# 空のデータフレーム
kihon = pd.DataFrame()
for indx in range(1, period+1):
if indx == 1:
remain = repay_amount * 10000
# 毎月の返済額
if fixfl == 0:
if np.mod(indx, 60) == 1 and indx > risemonth:
per1 = per1 + width_
repay_month = math.floor(npf.pmt(0.01*per1/12, period-indx+1, -remain))
# 毎月の利息
if np.mod(indx, 60) == risemonth_mod and indx > risemonth:
per2 = per2 + width_
interest = math.floor(npf.ipmt(0.01*per2/12, 1, period-indx+1, -remain))
else:
repay_month = math.floor(npf.pmt(0.01*per_fix/12, period, -repay_amount*10000))
interest = math.floor(npf.ipmt(0.01*per_fix/12, 1, period-indx+1, -remain))
# 毎月の返済額中の元本部分
principal = repay_month - interest
# 返済済
principal_acc += principal
# 当該月時点の残債
remain = repay_amount*10000 - principal_acc
kihon_new = pd.DataFrame([[indx, repay_month, interest, principal, principal_acc, remain, per1, per2]],
columns=["indx", "repay_month", "interest", "principal", "principal_acc", "remain", "per1", "per2"])
kihon = pd.concat([kihon, kihon_new])
kihon.loc[kihon["indx"]==period, "principal"] = kihon.loc[kihon["indx"]==period-1, "remain"]
kihon.loc[kihon["indx"]==period, "repay_month"] = kihon.loc[kihon["indx"]==period, "principal"] + kihon.loc[kihon["indx"]==period, "interest"]
kihon.loc[kihon["indx"]==period, "principal_acc"] = repay_amount*10000
kihon.loc[kihon["indx"]==period, "remain"] = 0
return kihon["repay_month"].sum(), kihon["interest"].sum(), kihon
# 空のデータフレーム
tbl = pd.DataFrame()
print("金利上昇開始が", riseyr , "年目で5年あたりの上昇幅が以下の場合、金利上昇が起きなかった場合と比べて")
for width in range(1, 60):
per_flu = 0.05*width
interest_sum = rise(riseyr, 0.05*width, 0)[1]
interest_sum_chg = rise(riseyr, 0, 0)[1]
interest_sum_fix = rise(riseyr, 0, 1)[1]
diff1 = interest_sum - interest_sum_fix
diff2 = interest_sum - interest_sum_chg
if diff1 > 0:
result = "固定勝利"
else:
result = "変動勝利"
tbl_new = pd.DataFrame([[per_flu, interest_sum, interest_sum_chg ,interest_sum_fix, diff1, result]], columns=["per_flu", "interest_sum", "interest_sum_chg", "interest_sum_fix", "diff1", "result"])
tbl = pd.concat([tbl, tbl_new])
print(f'{per_flu:.2f}', "%ならば" , '¥{:,.0f}'.format(diff2),"総返済額が増えます。")
tbl_1 = tbl.loc[tbl["result"]=="変動勝利"].tail(1)
tbl_2 = tbl.loc[tbl["result"]=="固定勝利"].head(1)
print("")
print("金利上昇開始が", riseyr , "年目の場合、5年あたりの上昇幅が" , f'{tbl_1["per_flu"].sum():.2f}', "%ならば総返済額は" , '¥{:,.0f}'.format(-tbl_1["diff1"].sum()),"変動金利がお得です。")
print("金利上昇開始が", riseyr , "年目の場合、5年あたりの上昇幅が" , f'{tbl_2["per_flu"].sum():.2f}' , "%ならば総返済額は" , '¥{:,.0f}'.format(tbl_2["diff1"].sum()),"固定金利がお得です。
<実行結果>
金利上昇開始が 5 年目で5年あたりの上昇幅が以下の場合、金利上昇が起きなかった場合と比べて
0.05 %ならば ¥758,887 総返済額が増えます。
0.10 %ならば ¥1,531,572 総返済額が増えます。
0.15 %ならば ¥2,318,220 総返済額が増えます。
0.20 %ならば ¥3,119,006 総返済額が増えます。
0.25 %ならば ¥3,934,062 総返済額が増えます。
0.30 %ならば ¥4,763,564 総返済額が増えます。
0.35 %ならば ¥5,607,613 総返済額が増えます。
0.40 %ならば ¥6,466,433 総返済額が増えます。
0.45 %ならば ¥7,340,144 総返済額が増えます。
0.50 %ならば ¥8,228,872 総返済額が増えます。
0.55 %ならば ¥9,132,823 総返済額が増えます。
0.60 %ならば ¥10,052,103 総返済額が増えます。
0.65 %ならば ¥10,986,860 総返済額が増えます。
0.70 %ならば ¥11,937,274 総返済額が増えます。
0.75 %ならば ¥12,903,466 総返済額が増えます。
0.80 %ならば ¥13,885,553 総返済額が増えます。
0.85 %ならば ¥14,883,675 総返済額が増えます。
0.90 %ならば ¥15,898,052 総返済額が増えます。
0.95 %ならば ¥16,928,719 総返済額が増えます。
1.00 %ならば ¥17,975,869 総返済額が増えます。
・・・
2.90 %ならば ¥71,088,653 総返済額が増えます。
2.95 %ならば ¥72,860,139 総返済額が増えます。
金利上昇開始が 5 年目の場合、5年あたりの上昇幅が 0.70 %ならば総返済額は ¥424,622 変動金利がお得です。
金利上昇開始が 5 年目の場合、5年あたりの上昇幅が 0.75 %ならば総返済額は ¥541,570 固定金利がお得です。
金利上昇開始が 15 年目で5年あたりの上昇幅が以下の場合、金利上昇が起きなかった場合と比べて
0.05 %ならば ¥260,888 総返済額が増えます。
0.10 %ならば ¥524,210 総返済額が増えます。
・・・
1.80 %ならば ¥11,045,433 総返済額が増えます。
1.85 %ならば ¥11,404,266 総返済額が増えます。
1.90 %ならば ¥11,766,081 総返済額が増えます。
1.95 %ならば ¥12,131,004 総返済額が増えます。
2.00 %ならば ¥12,498,874 総返済額が増えます。
2.05 %ならば ¥12,869,825 総返済額が増えます。
・・・
2.90 %ならば ¥19,657,213 総返済額が増えます。
2.95 %ならば ¥20,085,628 総返済額が増えます。
金利上昇開始が 15 年目の場合、5年あたりの上昇幅が 1.95 %ならば総返済額は ¥230,892 変動金利がお得です。
金利上昇開始が 15 年目の場合、5年あたりの上昇幅が 2.00 %ならば総返済額は ¥136,978 固定金利がお得です。まず、金利上昇開始時期が5年目と15年目で総返済額に大きな差があることをご確認頂ければと存じます。固定金利と比較した場合の損益分岐点に着目致しますと、金利上昇開始時期が5年目の場合は上昇幅が0.70〜0.75%の間、金利上昇開始時期が15年目の場合の損益分岐点は上昇幅が1.95〜2.00%の間にあることが分かります。後者の場合は35年目で8%に達する計算でして、これはバブル期と同水準であることを意味しております。
4.結言
今回は住宅ローンの金利上昇時の総返済額への影響についてシミュレーション致しました。プログラムとしては5年ルールの処理が最も手を焼いたものの、上昇時の金利が利息へ反映されるタイミングと返済額へのタイミングが同じでない点を学ぶことができ、収穫がありました。
さて、返済計画という点においては金融のプロのご見解の中には固定金利を推す方も多いと思いますが、現在は歴史的な低金利で推移しておりますため、この恩恵を最大限に享受しておくべきというのが個人的な考えとしてございます。そのため契約時は変動金利を選択し、利息の割合が大きい返済初期に返済を進めておく(残債を減らしておく)ことが重要であり、返済終盤の金利上昇が大きな痛手にならないことは本シミュレーションが示しております。本シミュレーションを逃げ切る(金利上昇時の家計負担を最小限に留める)ための一ツールとしてご活用頂けますと嬉しく思います。ただし、その際は軍資金(繰上げ返済資金)の準備が条件と考えます。後編ではこのあたりを詳細に検証していく予定でございます。次回以降もご期待頂ければと存じます。
尚、本プログラムはご自身の責任においてご利用頂けますようお願いいたします。当社はいかなる損害についても一切の責任を負いかねます。
免責事項は以下の記事に記載しております。
ここまでお読みいただき、ありがとうございました!
この記事が少しでも参考になりましたら「スキ」を押していただけると幸いです!
これまでの記事はこちら!
株式会社分析屋について
弊社が作成を行いました分析レポートを、鎌倉市観光協会様HPに掲載いただきました。
ホームページはこちら。
noteでの会社紹介記事はこちら。
【データ分析で日本を豊かに】
分析屋はシステム分野・ライフサイエンス分野・マーケティング分野の知見を生かし、多種多様な分野の企業様のデータ分析のご支援をさせていただいております。 「あなたの問題解決をする」をモットーに、お客様の抱える課題にあわせた解析・分析手法を用いて、問題解決へのお手伝いをいたします!
【マーケティング】
マーケティング戦略上の目的に向けて、各種のデータ統合及び加工ならびにPDCAサイクル運用全般を支援や高度なデータ分析技術により複雑な課題解決に向けての分析サービスを提供いたします。
【システム】
アプリケーション開発やデータベース構築、WEBサイト構築、運用保守業務などお客様の問題やご要望に沿ってご支援いたします。
【ライフサイエンス】
機械学習や各種アルゴリズムなどの解析アルゴリズム開発サービスを提供いたします。過去には医療系のバイタルデータを扱った解析が主でしたが、今後はそれらで培った経験・技術を工業など他の分野の企業様の問題解決にも役立てていく方針です。
【SES】
SESサービスも行っております。
