【勉強の秋編(その2)】電磁気演習問題解説(自習用):相対論
技術者にとって、実務での応用力や発想力を伸ばして行くためには、知識や技術の裾野を広げ続けることが必須であり、専門技術分野の深耕+関連技術分野も分野横断的に修得することにより、新技術・新製品を開拓する総合技術者であることが重要となります。
例えば、電気・電子系の技術者でも、製品に依っては、材料科学や伝熱工学等の分野横断的な見識を持ち、複合技術から新しい技術を創造する鍛錬が必要な場合も多く存在しています。
【参考文献】
電磁気学は、4つの法則ががっちりスクラムを組んで、綻びのない理論体系を作り上げています。
この電磁気学には、私たちの好奇心を掻き立ててくれる不思議が随所に隠れています。
ここでは、電磁気学の奥深いところを覗いてみるのも、もしかしたら面白いのではないかと思い立ち、相対性理論との関係を取り上げて、実際の問題を解いてみることで、そのリアルな世界を、感じて頂ければと思います(^^)
【概要】
さて、ニュートン力学が絶対視されていた19世紀。
慣性系座標変換の規範となっていたガリレイ変換をマクスウェルの方程式に適用すると、厳密には成立しない問題がありました。
そのため、電磁気学は、当時、近似の理論と見なされていたんです。
アインシュタインは、この点に着目し、電磁気学の方に真実があることを見抜き、ニュートン力学を近似理論とする特殊相対性理論を作り上げました。
その理論が規範とした座標変換は、ローレンツ変換です。
本記事では、マクスウェルの方程式が、ローレンツ変換に対して不変であること(共変性を有すること)を問題を解く事で簡単に触れてみますね。
電磁気学は、20世紀に吹き荒れた相対性理論による力学革命の嵐を無傷で乗り越え、現代の力学理論の一翼を担っています。
【要旨】
物理法則は、ある範囲内で、いつでも、どこでも、ある程度は普遍的・恒常的に、その形を保つのでなければ法則の名に値しません。
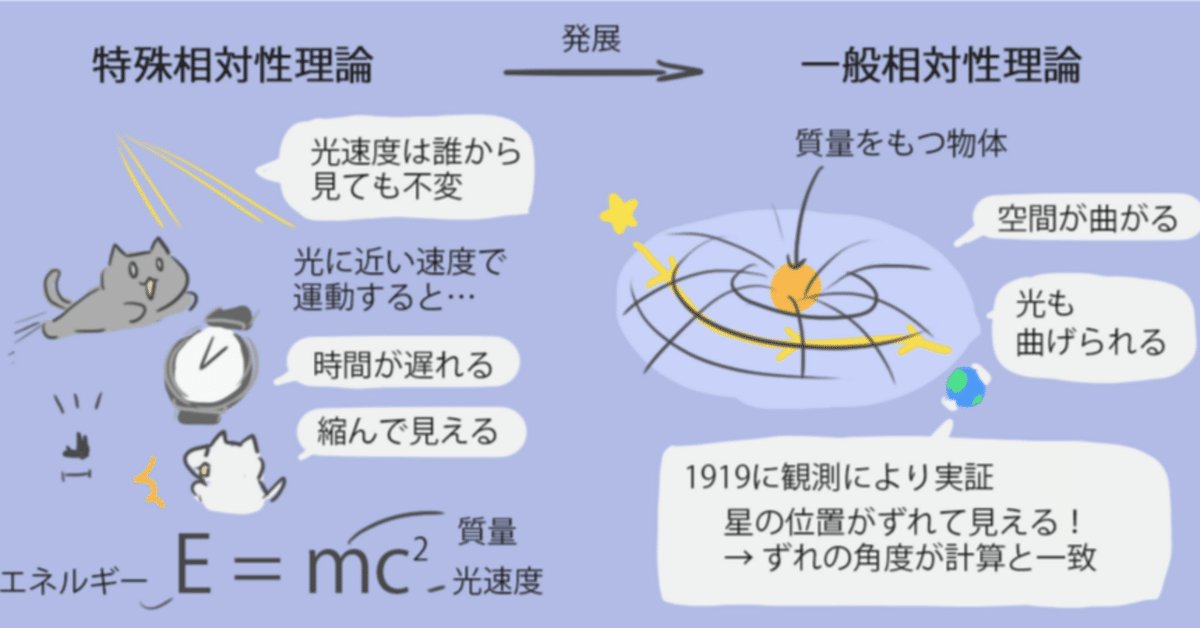
そこで、アインシュタインは「互いに等速度運動するすべての基準系で物理法則は同じ形式を持つ」ことを先験的に認めるよう主張しました。
これをアインシュタインの特殊相対性原理といいます。
この原理の精神に従えば、「どの慣性系(特殊相対性理論では、マックスウェル方程式が成り立つ基準系を慣性系と呼んでいます。)でも、真空中の光速は、光源の運動状態に関係なく、全ての方向へ同じとなる」と考えられます。
これを光速不変の原理といいます。
これら2つの原理に基づいてたてられた理論が特殊相対性理論です。
今回の演習では、まず、相対論的な時空の性質を座標変換式は時空を反映することから、どのような変更になっているかをローレンツ変換式から調べます。
これは、19世紀末に、真空放電内で電子が発見され、その運動が詳しく研究されて、ニュートン方程式でけいさんされた電子の運動と実験結果とが電子の速度が大きくなるにつれて、偏差を生じることが明らかとなってきました。
すなわち、低速の間は、両者がよく一致するのに対して、速さが光速に近くなると、電子の質量が増大したと解釈されるような偏差が現れてきました。
まず、ニュートンの運動方程式は、ガリレイ変換に対して不変です。
つまり、マックスウェルの電磁方程式がローレンツ変換に対して不変であるというのは、力学法則と電磁法則とが異なる座標変換式に従うことになり、荷電粒子の運動のように、両法則が関与する問題に対して不都合が生じてしまいます。
その結果、ローレンツ変換に対し不変なマックスウェル電磁方程式は、そのまま残すことにしました。
そして、新しい運動方程式として、ローレンツ変換に対して不変で、速度が小さい極限では、ニュートン方程式に近づくように、相対論的な運動方程式をもとめることを考えつきます。
最後に、加速器は、科学技術の広い分野において重要な基礎技術であり、今回の演習の終わりに、電子貯蔵リングに焦点を当て、放射光の一般的性質について、実際に、シンクロトロン放射によるエネルギー損失と粒子のエネルギーについて計算してみました。
【電磁気演習問題:相対論】
3次元静止座標系A(x、y、z)に対して、x方向に一様な速度vで運動している座標系B(x’、y’、z’)を考える。
注:式中の数字は、基本的に累乗(以下同様)です。
設問(1):
座標系Aから座標系Bへのローレンツ変換
x’=γ(x-vt)、y’=y、z’=z、t’=γ(t-vx/c2)
およびローレンツ逆変換
x=(1-v2/c2)-1/2
を導け。
設問(2):
ローレンツ変換より、座標系Aでのy方向加速度と座標系Bでのy’方向加速度がV’x=0の状況で、
d2y’/dt2=γ2(d2y/dt2)
となることを導け。
設問(3):
垂直方向の一様磁界Bにより、光速に限りなく近い速度(99.999%程度)で周回運動している電子が径方向の加速度で制動放射(シンクロトロン放射)する場合の単位時間当りの損失エネルギーが、
P=(1/6πε0)(e4/m4c5)B2E2
となることを導け。
但し、加速度aを受ける電子の制動放射
P=(1/6πε0)(e2a2/c3)
電子のエネルギー
E=γmc2
を用いよ。
また、半径ρの円周を一周する間に損失するエネルギーが
U0[keV]=88.5E4[GeV]/ρ[m]
となることを導け。
悲劇の加速器と言われた日本の電子、陽電子衝突型加速器TRISTANは、30GeVのエネルギーで周長3km、コーナーの曲率半径は平均半径の約半分である。
損失エネルギーはビームエネルギーの何%か。
また、同じ損失エネルギー比で100GeVの電子リングを設計すると周長は何kmになるか求めよ。
【問題の説明】
何事も同じだと考えますが、疑問に思った瞬間に行動を起こさないと、本人にとっては、永遠の疑問になってしまうものだと思いますので、例えば、今回の設問に対する参考図書としては、古い本ですが、以下が参考になると思います。
<参考図書>
「場の古典論(原書第6版)」 (ランダウ=リフシッツ理論物理学教程) エリ・ランダウ/イェ・エム・リフシッツ(著)恒藤敏彦(訳)

「加速器ハンドブック」日本加速器学会(編)

<参考記事>
設問(1):
・四元ベクトルを使ったか?:時間と空間の融合を理解したか?
・γ>0を考察したか?:時間の非可逆性に疑問を持ったか?
設問(2):
・ローレンツ変換数学的扱い:tとt’を混乱していないか?
・速度のローレンツ変換を理解したか?
・加速度のローレンツ変換を理解したか?
設問(3):
・制動放射の相対論的扱い:aとa’を混乱していないか?
・大型電子加速器の理解:平均半径の考え方を理解したか?
・接線方向へ亜速度を受ける場合の制動放射は?
・大型陽子加速器設計ではどうか?
【解答例】
設問(1)の解答例:
この問題は、一見、ただの計算演習だが、式の意味を良く考え、常日頃、当たり前と思っている事を考察してみることを想定している。
まず、基準座標系Sに対して、x方向にvで動く座標系S’へのローレンツ変換を行列変換の形で表現してみる。(注:表記上、行列式の[]は、省略(以下同様)しています。)
X' γ 0 0 -γv x
y' = 0 1 0 0 * y 式(1)
z' 0 0 1 0 z
t' -γv/c2 0 0 γ t
ここで、ミフコンスキーがやったように、このベクトルに物理的な意味を持たせてみます。
つまり、唯一の絶対速度「光速度」が見つかったことにより、座標と時間を同じベクトルの成分として扱うことが可能になります。
結論を急ぐためにtの代わりに、jct(jは虚数単位)を使用します。
このような座標成分をとることによって、ベクトルの大きさは、式(2)に示す通り、座標系によらず不変量となる。
s=√X2+y2+Z2-C2t2 式(2)
このようなベクトルを4元ベクトルと言い、4元ベクトルで表される点を世界点、2つの世界点の距離を世界感覚と呼んでいる。
ベクトルの大きさsは、ある原点から、ある世界点までの世界間隔となる。
世界間隔が不変量となるのは、世界点を光が伝搬した点ととることによって座標系に拠らず、必ずゼロになることから明らかである。
この世界間隔で不変量という条件だけからローレンツ変換は導けるが、興味が有る方は、是非、やってみて下さい。(ベクトルの大きさが不変量となる変換は、回転変換であることを思い出して頂ければ解けるのではないかと思います。)
さて、問題に戻って、今、変換に影響しないy及びz軸を省力すると、式(3)が導けます。
X' γ jγv/c x
= * 式(3)
ict' -jγv/c γ jct
同様に、ローレンツ逆変換は、
X γ - jγv/c x'
= * 式(4)
ict jγv/c γ jct'
と書けるため、式(3)と式(4)から、
γ jγv/c γ - jγv/c 1 0
* = 式(5)
-jγv/c γ jγv/c γ 0 1
となり、
γ2-(γ2v2/C2)=1、
γ=±√(1-(v2/c2) 式(6)
を得る。
さて、ここからが少し難しくなる。
まず、x座標が実数であることから、v<cでなければならない。
つまり、光速度より早く移動する座標系へのローレンツ変換(逆に、ローレンツ変換で定義づけられる世界では、光速度より早い速度のもの)は許されない。
また、ある事象に対する絶対的未来、絶対的過去及び絶対的隔離領域が定義できることになる。
これは、ある事象O(原点)に因果関係を与えられるのは、x=±ctで囲まれた領域だけであること。
つまり、光速度以下の伝達手段でのみO点(原点)との世界線(複数の世界点の連続)を結ぶことが可能となっていることから理解できる。
これは光円錐と呼ばれている。
<参考文献>
ミンコフスキー時空
https://mcm-www.jwu.ac.jp/~physm/buturi17/soutaisei/minko.html
今、ゼロでない世界間隔を持つ事象が絶対的未来に存在するとき、世界間隔は保持されるため、世界間隔がゼロの原点へローレンツ変換するのは不可能である。
従って、時間的に隔たった事象は、いかなる座標系をとっても、同時には起こり得ない。
変換の一般性から、絶対的未来の事象は、いかなる座標系をとっても絶対的過去には起こり得ない。
これが、式(6)でプラスをとる意味である。
γ=±√1-(v2/c2) 式(7)
さて、ここで、解答例として、v=0でx’=x、t’=tという条件からγ>0を結論付けてしまうと、これでは数学的には根拠がないことになる。
つまり、マイナスの座標軸へ写像してはいけないという制限は、どこにもないことになるからである。
敢えて言うなら、極限として古典力学のガリレオ変換にならねばならないと答えるべきである。
但し、これはガリレオ変換でマイナスの時間の議論が充分されていないだけで、やはり、数学的には根拠がない。
こういう一見、当たり前の問題に直面した時には、何がわかっていて、何が議論として残っているかを洞察することが、科学を進歩させる力になるので、決して常識や感覚に流されないように注意する必要がある。
設問(2)の解答例:
ローレンツ逆変換の変分をとる。
δx=(δx'+vδt')/√(1ー(v2/c2)、
δy=δy'、
δz=δz'、
δt=(δt'+(v/c2)δx')/√(1-(v2/c2)) 式(8)
δtで割り、その極限として静止座標系Aでの速度を求める。
dx/dt
=δx'+vδt'/(δt'+(v/c2)δx')
=v'x+v/(1+((v・v'x)/c2))
dy/dt
=(δy√1-(v2/c2)/δt'+((v/c2)δx')
=v'y/(1+(v・v'x)/c2))・(1/γ)
dz/dt
=δz√1ー(v2/c2)/δt'+((v/c2)δx')
=v'z/(1+((v・v'x)/c2))・(1/γ) 式(9)
これが速度に関する逆ローレンツ変換である。
式(9)の変分をとる。
δvx=
((δv'x・(1+(v・v'x)/c2)))ー((v'x+v)・((v・δv'x)/c2))))/(1+((v・v'x)/c2))2
=(δv'xー((v2・δv'x)/c2))/(1+((v・v'x)/c2))2
=(δv'x/(1+((v・v'x)/c2))2・(1/γ2)
δvy=((δv'y・(1+((v・v'x)/c2)))ー(v'y・((v・δv'x)/c2)))/(1+((v・v'x)/c2))2・(1/γ)
δvz=((δv'z・(1+((v・v'x)/c2)))ー(v'z・((v・δv'x)/c2)))/(1+((v・v'x)/c2))2・(1/γ) 式(10)
δtで割り、その極限として静止座標系Aでの加速度を求める。
dvx/dt
=δv'x/(δt'+((v/c2)・δX'))・γ・(1+((v・v'x)/c2))2・(1/γ2)
=(dv'x/dt')/(1+((v・v'x)/c2))3・(1/γ3)
dvy/dt
=(((δv'y・(1+((v・v'x)/c2)))ー(v'y・((v・δv'x)/c2)))/(δt'+((v/c2)・δX'))・γ・(1+((v・v'x)/c2))2・(1/γ)
=((dv'y/dt・(1+((v・v'x)/c2)))ー((v'y・v/c2)・(dv'x/dt')))/(1+((v・v'x)/c2))3・(1/γ2)
dvz/dt
=(((δv'z・(1+((v・v'x)/c2)))ー(v'z・((v・δv'x)/c2)))/(δt'+((v/c2)・δX'))・γ・(1+((v・v'x)/c2))2・(1/γ)
=((dv'z/dt・(1+((v・v'x)/c2)))ー((v'z・v/c2)・(dv'x/dt')))/(1+((v・v'x)/c2))3・(1/γ2) 式(11)
これが加速度に関するローレンツ変換である。
v'x=0、dv'x/dt=0
の条件で書き直すと以下となる。
dvx/dt=dv'x/dt'・(1/γ3)
dvy/dt=dv'y/dt'・(1/γ2)
dvz/dt=dv'z/dt'・(1/γ2) 式(12)
従って、以下を得る。
d2y'/dt'2=γ2・d2y/dt2 式(13)
設問(3)の解答例:
加速度aを受ける電子の制動放射
P=(1/(6πε0))・((e2・a2)/c3) 式(14)
において、加速度aは、周回運動する電子の接線方向(x)の速度で移動する慣性系の径方向(y’)加速度a'とみなすことができる。
今、実験室系の加速度aで、式(14)を書き直すと式(13)により下記となる。
P=(1/(6πε0))・((e2・a2)/c3)・γ4 式(15)
半径ρで光速に限りなく近い速度で円運動する電子に関し、下記を用いる。
a=v2/ρ≒c2/ρ、ρ=(m・v・γ)/(e・B)≒(m・c・γ)/(e・B) 式(16)
P=(1/(6πε0))・((e2・c)/ρ2)・γ4
=(1/(6πε0))・((e4・B2)/(m4・c))・γ2
=(1/(6πε0))・(e4/(m4・c5))・B2・E2 式(17)
また、BをρおよびEで書き直すと、下記のようになる。
P=(1/(6πε0))・(e2/(m4・c7・ρ2))・E4 式(18)
ここで、電子の古典半径を導入する。
r0=(1/(4πε0))・(e2/(m・c2))=2.818×10-15m 式(19)
従って、一周あたりに損失するエネルギーは下記となる。
U0=P・(2πρ)=(4π/3)・(r0/(mc2)3)・(E4/ρ)=8.85×10-5(m/(GeV3))・(E4/ρ) 式(20)
日本の電子・陽電子衝突型加速器TRISTANは、30GeVのエネルギーで周長3km(半径にして約500m)だが、U0=143MeVとなる。
実際には、円弧の半径は、約1/2であり、U0=300MeVとなり、ビームエネルギーの1%である。
仮に、100GeVのビームエネルギーのシンクロトロンを同じエネルギー効率(放射エネルギーがビームエネルギーの1%)で設計しようとすると、半径は9km」(周長56km)の巨大なものになってしまう。
そのちょうど半分(周長27km)の加速器が電子サイクロトロンの限界(その当時)と言われるECのLEPである。
<参考文献>
【関連記事】
【食欲の秋編(兼読書の秋)】おいしい酒の肴
https://note.com/bax36410/n/n4f91f559aea6
【紅葉の秋編】紅い天井、真っ赤なじゅうたん。
https://note.com/bax36410/n/nd7e55e4d2186
【美術の秋編(その1)】足立美術館の名園とともに名画を観る
https://note.com/bax36410/n/n6d41c14be8aa
【美術の秋編(その2)】足立美術館が誇る主庭「枯山水庭」
https://note.com/bax36410/n/n7543cb7de2b2
【勉強の秋編(その1)】扉を開けると、世界が広がる!
https://note.com/bax36410/n/n1b284b20cc98
【読書の秋編】ボルツマンの原理(熱力学と統計力学)を理解しよう
https://note.com/bax36410/n/n2f1477f95dfc
【睡眠の秋編(兼読書の秋)】生物時計と睡眠の遺伝子について学んでみた
https://note.com/bax36410/n/nd4d37bf5339a
【収穫の秋編(兼読書の秋)】不可能を可能にした自然栽培と「奇跡のリンゴ」
https://note.com/bax36410/n/n494e744b4687
【旅行の秋編(その1)】ブロードウェイでミュージカル「マンマ・ミア!」を観る
https://note.com/bax36410/n/ne32be3fe2d1f
【旅行の秋編(その2)】海外の風景:スタッテン島行きフェリー
https://note.com/bax36410/n/nd76fa68be7dd
【行楽(レジャー)の秋編(その1)】真剣に遊ぶ男(大人)=闘う男論
https://note.com/bax36410/n/n15b36a3c5332
【行楽(レジャー)の秋編(その2)】大人の探検ごっこ
https://note.com/bax36410/n/na59f4997dd19
【ファッションの秋編】やっぱり青が好き
https://note.com/bax36410/n/nd8ac6b3998d9
【運動(スポーツ)の秋編】風に乗ってパラグライダーで飛ぶ!
https://note.com/bax36410/n/n4fa51a036e2a
【実りの秋編】「NO RICE NO LIFE」
https://note.com/bax36410/n/nb57c659657e6
【音楽の秋編】音楽の講義が聞きたい
https://note.com/bax36410/n/n73cad903467f
