数学を分けて「読む」
みなさんこんにちは!あしまるです!
さて、本日の記事は数学を分けて「読む」です。え?数学なのに読むの?と思った方。数式君だって伝えたいことがあるんですよ、本当は!!その「伝えたいこと」を読み取れるようになれば、数学は宇宙語じゃなくなるはずです。
そこで、今回は高校数学における必須テクニック「平方完成」をできるだけ最短ルートで処理する方法を考えていきます。この方法はものぐさ高校生(中学生)あしまるくんが、平方完成を丁寧にやりたくなくて編み出した(?)ものを、あしまる先生がきちんと整理整頓したものです。あしまる式なんて言っても、ものぐさ高校生が編み出すぐらいなので、間違いなくどっかの偉い先生も思いついているでしょう。しかし、今回大切なのは「情報を区切って理解する」ということですのであしからず。
1.超高速!あしまる式?平方完成
まあ大体の人は「平方完成が超高速で出来るなら教えてくれ!」と思うでしょうから、先に説明します。いろいろ方法はあると思いますので、今の自分のやり方で十分だと思う人は参考までに。もしかしたらもっと早い方法もあるかもしれないですからね!逆に平方完成が遅すぎてつらい人はぜひ活用してください。
あしまる式を使用するにあたって用意するものは、下にある分数の棒線(括線というらしい)と-1を含んだ掛け算の式だけです。
用意するもの(1)
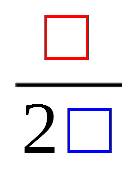
用意するもの(2)
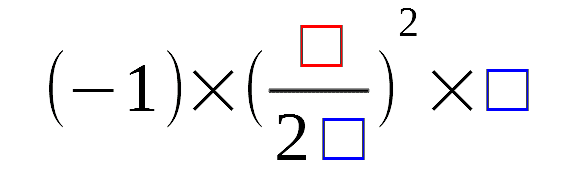
今回はy=2x² -6x+1を平方完成してみましょう。
【手順①】x² の前についている数字を前に出して( x - )² を用意。
【手順②】用意するもの(1)に入れるべき数字を放り込んで計算します
【手順③】手順②で出てきた数字を用意するもの(2)に放り込んで計算します
【手順④】最後に+1を添えて、あとは計算できるところを計算しておしまい
画像で示すと以下のようになります。
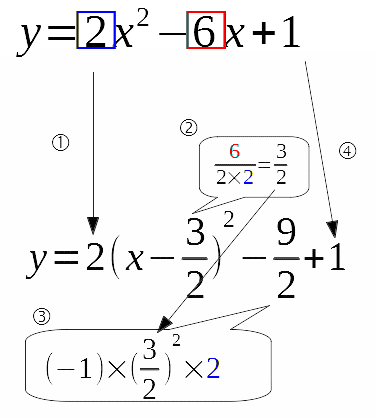
早い話が、吹き出し②と③の部分をどっか余白に計算するなり暗算するなりして、入れるべき場所に書き込めば、ほぼほぼ完成形が見えてしまうってことなんです。この変形に途中式を記述せねばならない理由なんてありませんから、突然この式が誕生しても何の問題もありません。②の計算も③の計算も中1ぐらいの計算ですから、慣れれば暗算も簡単です。しかも、③の計算をするときは、③以外見なくていいのですから、話は一気に単純化するはずです。
2.あしまる式?の仕組み
ここまで読んだ皆さんの中には、こう思った人もいるはずです。「いや、y=ax²+bx+cを平方完成した式に代入しているだけでは?そんなの今どきの参考書ならどこにでも書いてあるよ」と...
いや、まったくもってその通りなんです!笑
解の公式とやってることがぱっと見では変わらないですね!
でも、この事実に気づいたのは高校を卒業してからでした。つまり、「式を一般化して、いつでも使えるような公式として平方完成しよう」と考えたわけではないんです。「平方完成という計算を分解して読んだ結果、計算はこれだけでいいのでは?」と気づいたのです。
私は、平方完成のやり方自体は通常通り式変形していく方法で習っています。しかし、同時にこの事実を習いました。
「この解法の発想は『足りないものは足して引けば元通り』ということ。勉強した乗法公式を使うために必要な数字を探って解いている!」
そう、平方完成を初めて習ったとき、平方完成自体は全くの新しい知識ではなく、既習の知識を使うための考え方なのだと知ったのです。それがわかると、あしまる式平方完成の意味もわかってきます。上にあるあしまる式というのは実は
(1)前半2項(2x² -6x)に区切って、【乗法公式:( x + a )² = x² + 2ax + a² 】を適用【手順①、②】
(2)出てきた軸の部分を使って、【足りないものは足して引けば元通り】を適用【手順③】
という考えで計算をしていたんです。分けて見て、部分的に暗算するために計算を最適化しているんですね。
元々この方法が編み出されたのは、バスの中で宿題をするせいで、あんまり書きたくないから暗算しやすいように考え直しただけ、というとんでもない理由だったのですが...さすがものぐさ学生...
3.知っていることを探し出し、分解する
2.で紹介した思考パターンは、おそらく人によって異なっていく部分ではあると思います。しかし、「自分の知っていることを探し出す」という姿勢は、学習において必要不可欠です。私の授業ではよく「なぜ?」とか「なにをやっているのか?」とかそういう問いかけを多く行います。この問いかけは「今の自分の知識を使ってみたときに、どんな予測が立つか?」を考えてもらうための質問でもあったのです。新しい学びを、自分の知識の延長に置くことができないと、「新しい」が多すぎて脳がパンクします。
自分の知っていることを探すことが、情報を整理する重要な手掛かりになるんです。例えば私は、数学IIIをほぼ独学で勉強しましたが、この時に「知識探し」をしました。最初のページである「複素数平面」のページを開いてみたときにすぐ考えたことは「今の知識を無理やり適用したらどうなる?」ということ。そうやって「自分の知っていること」を探し出していった結果、新しいことはとりあえず「今までの座標P(a,b)がz = a + biで表示されて、複素数そのものを考えることができる平面になってる」と考えて、問題を解いていきました。知っているところは、もうある程度自信をもって考えられますから、新しいことだけに集中できるようになっていったんですね!
どんな学習も、完全に新しい知識だけということはありません。必ず自分の知っていることが隠れているはずなんです。あなたも「自分が知っていること」を探そうとするだけで、今まで難しく感じていた1つのことが、分かれた情報になっていくはずです。数学に限らず、「分けて読む」というのがいかに重要か、少しでもつかんでいただければ幸いです。
