ラプラス変換によるRL直列回路の解法(交流電源の場合)

図1.RL直列回路(交流電源)

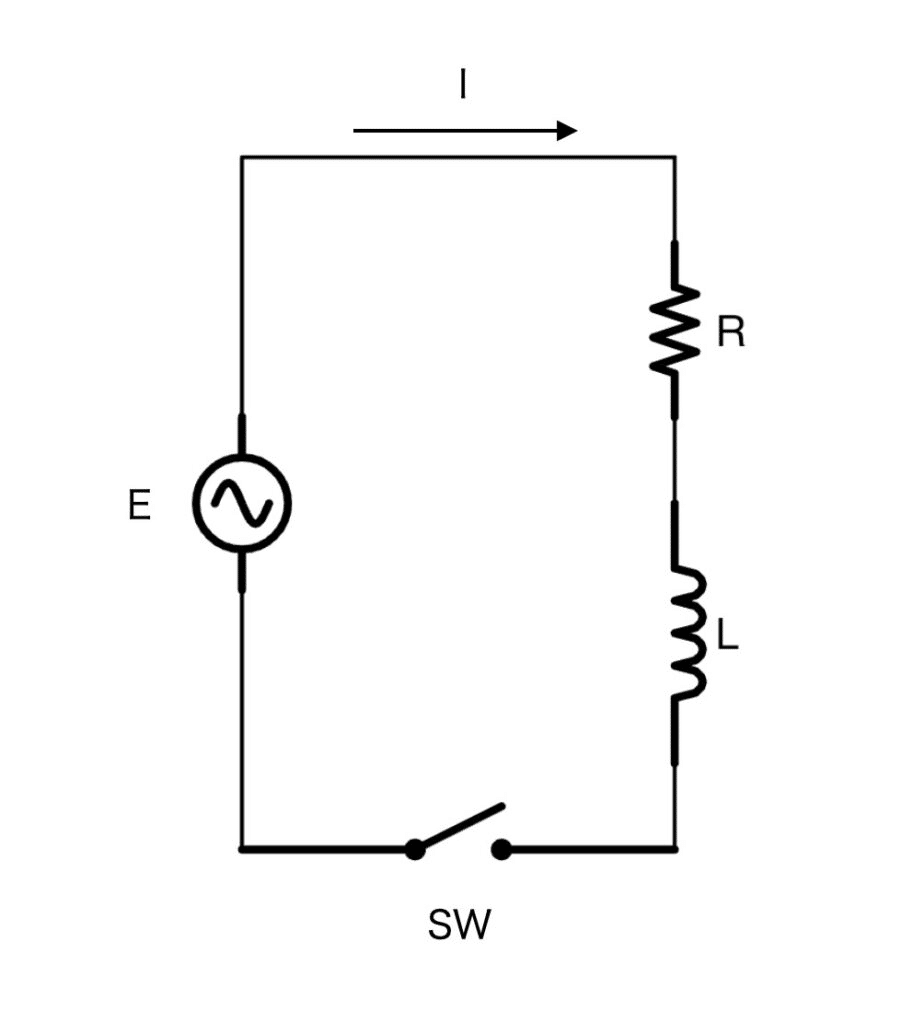
今、図1のようなRL直列回路を考え、交流電源をEとして、スイッチを入れてからt秒後に流れる電流Iを求める方法について考えてみます。
今、図1の回路において、回路方程式

$${\Large RI+L\frac{dI}{dt}=E_m\sin\omega t\hspace{50pt}(1)}$$

が成り立ちます。今、

$${\Large RI+L\frac{dI}{dt}=E_m\sin\omega t=f(t)}$$

としてf(t)のラプラス変換を

$${\Large F(s)=\mathcal{L}f(t)}$$

とします。(1)式の両辺をラプラス変換すると

$${\Large RI(s)+L\{sI(s)-I(0)\}=E_m \frac{\omega}{s^2+\omega^2}}$$

電流の初期値I(0)=0とすると、

$${\Large RI(s)+LsI(s)=E_m \frac{\omega}{s^2+\omega^2}\hspace{50pt}(2)}$$

(2)式をI(s)について解くと、

$${\Large I(s)=\frac{\omega E_m}{(R+Ls)(s^2+\omega^2)}\hspace{50pt}(3)}$$

(3)式の右辺をLで割ると

$${\Large I(s)=\frac{\frac{\omega E_m}{L}}{(s+\frac{R}{L})(s^2+\omega^2)}}$$

等式変形して

$${\Large \frac{L}{\omega E_m}I(s)=\frac{1}{(s+\frac{R}{L})(s^2+\omega^2)}\hspace{50pt}}$$

$${\Large \frac{L}{\omega E_m}I(s)=\frac{1}{(s+\frac{R}{L})(s+j\omega)(s-j\omega)}\hspace{50pt}(4)}$$

ここで(4)式の右辺を部分分数分解するために

$${\Large \frac{1}{(s+\frac{R}{L})(s+j\omega)(s-j\omega)}=\frac{\alpha}{s+\frac{R}{L}}+\frac{\beta}{s+j\omega}+\frac{\gamma}{s-j\omega}\hspace{50pt}(5)}$$

$${\Large =\frac{\alpha(s+j\omega)(s-j\omega)+\beta(s+\frac{R}{L})(s-j\omega)+\gamma(s+\frac{R}{L})(s+j\omega)}{(s+\frac{R}{L})(s+j\omega)(s-j\omega)}\hspace{30pt}(6)}$$

今、分母を揃えたので、分子の値が一致すれば良いので、(5),(6)式から

$${1=\alpha(s+j\omega)(s-j\omega)+\beta(s+\frac{R}{L})(s-j\omega)+\gamma(s+\frac{R}{L})(s+j\omega)\hspace{10pt}(7)}$$

であれば良いです。
α,β,γを求めるために、(7)式のsに適当な値を代入します。
簡略化の為に$${\frac{R}{L}=X}$$とおきます。

①$${s=-jω}$$を代入すると

$${\large {1=-2j\omega \beta(X-j\omega)\hspace{50pt}}}$$

$${\Large \beta=-\frac{1}{2j\omega(X-j\omega)}\hspace{50pt}}$$

ここで

$${\large Z=X-j\omega \hspace{50pt}}$$

とすると（図2を参照）

$${\large Z=|Z|e^{j\varphi}\hspace{50pt}}$$

より

$${\Large \beta=-\frac{1}{2j\omega \sqrt{X^2+\omega^2}e^{-j\varphi}}\hspace{50pt}}$$

$${\Large =-\frac{e^{j\varphi}}{2j\omega \sqrt{X^2+\omega^2}}\hspace{50pt}(8)}$$

図2.共役複素数

②$${s=jω}$$を代入すると

$${\large 1=2j\omega \gamma(X+j\omega)\hspace{50pt}}$$

$${\Large \gamma=\frac{1}{2j\omega(X+j\omega)}\hspace{50pt}}$$

$${\Large =\frac{1}{2j\omega \sqrt{X^2+\omega^2}e^{j\varphi}}\hspace{50pt}}$$

$${\Large =\frac{e^{-j\varphi}}{2j\omega \sqrt{X^2+\omega^2}}\hspace{50pt}(9)}$$

③$${s=-\frac{R}{L}}$$を代入すると

$${\large 1=\alpha(-X+j\omega)(-X-j\omega)\hspace{50pt}}$$

$${\Large \alpha=\frac{1}{(X-j\omega)(X+j\omega)}\hspace{50pt}}$$

$${\Large =\frac{1}{X^2+\omega^2}\hspace{50pt}(10)}$$

(5)式に求めた$${\alpha,\beta,\gamma}$$を代入すると

$${\Large \frac{L}{\omega E_m}I(s)=\frac{1}{(X^2+\omega^2)(s+X)}-\frac{e^{j\varphi}}{2j\omega \sqrt{X^2+\omega^2}(s+j\omega)}+\frac{e^{-j\varphi}}{2j\omega \sqrt{X^2+\omega^2}(s-j\omega)}}$$

$${I(s)}$$$${=}$$$${\Large \frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{1}{\sqrt{X^2+\omega^2}(s+X)}-\frac{e^{j\varphi}}{2j\omega(s+j\omega)}+\frac{e^{-j\varphi}}{2j\omega(s-j\omega)}\biggr\}\hspace{50pt}(11)}$$

(11)式の両辺をラプラス逆変換すると

$${\mathcal{L^{-1}}I(s)}$$$${=}$$$${\Large \frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{e^{-Xt}}{\sqrt{X^2+\omega^2}}-\frac{e^{j\varphi}e^{-j\omega t}}{2j\omega}+\frac{e^{-j\varphi}e^{j\omega t}}{2j\omega}\biggr\}}$$

$${\Large =\frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{e^{-Xt}}{\sqrt{X^2+\omega^2}}+\frac{e^{j(\omega t-\varphi)}-e^{-j(\omega t-\varphi)}}{2j\omega}\biggr\}\hspace{30pt}(12)}$$

ここでオイラーの公式より

$${\large e^{j(\omega t-\varphi)}=\cos(\omega t-\varphi)+j\sin(\omega t-\varphi)\hspace{30pt}(13)}$$

$${\large e^{-j(\omega t-\varphi)}=\cos(\omega t-\varphi)-j\sin(\omega t-\varphi)\hspace{30pt}(14)}$$

$${※\cos(-\theta)=\cos\theta,\hspace{10pt}\sin(-\theta)=-\sin\theta}$$

(13)+(14)を計算すると

$${\large e^{j(\omega t-\varphi)}+e^{-j(\omega t-\varphi)}=2\cos(\omega t-\varphi)}$$

$${\large \cos(\omega t-\varphi)}$$$${=}$$$${\Large \frac{e^{j(\omega t-\varphi)}+e^{-j(\omega t-\varphi)}}{2}\hspace{50pt}(15)}$$

(13)-(14)を計算すると

$${\large e^{j(\omega t-\varphi)}-e^{-j(\omega t-\varphi)}=2j\sin(\omega t-\varphi)}$$

$${\large \sin(\omega t-\varphi)}$$$${=}$$$${\Large \frac{e^{j(\omega t-\varphi)}-e^{-j(\omega t-\varphi)}}{2j}\hspace{50pt}(16)}$$

(16)式より(12)式は

$${\Large =\frac{\omega E_m}{L\sqrt{X^2+\omega^2}}\biggl\{\frac{e^{-Xt}}{\sqrt{X^2+\omega^2}}+\frac{\sin(\omega t-\varphi)}{\omega}\biggr\}\hspace{30pt}(17)}$$

$${\Large =\frac{\omega E_m}{L\sqrt{\frac{R^2}{L^2}+\omega^2}}\biggl\{\frac{e^{-\frac{R}{L}t}}{\sqrt{\frac{R^2}{L^2}+\omega^2}}+\frac{\sin(\omega t-\varphi)}{\omega}\biggr\}\hspace{30pt}(18)}$$

$${\Large =\frac{E_m}{\sqrt{R^2+\omega^2L^2}}\biggl\{\frac{\omega L}{\sqrt{R^2+\omega^2L^2}}e^{-\frac{R}{L}t}+\sin(\omega t-\varphi)\biggr\}}$$

$${\Large =\frac{E_m}{\sqrt{R^2+\omega^2L^2}}\biggl\{\sin(\omega t-\varphi)+e^{-\frac{R}{L}t}\sin\varphi\biggr\}\hspace{30pt}(19)}$$

(19)式の第一項は定常状態で流れる電流値、第二項の指数関数がついている項はスイッチを入れた瞬間に流れる過渡的な電流値であり、t→∞の時、0になります。

RL直列回路(直流電源)の場合と比べて、ラプラス変換を用いたとしても、計算が結構大変。

最後まで読んでいただいてありがとうございました。