科学と統計
AKIRAです。
本日は、私がちょっと気になったお話について。
統計は、厳密には因果関係を証明するものではない
サブタイトルにもある通り、統計は因果を証明するためのツールではありません。正確には、「異なる事象の相関関係を示す」ことが目的です。

図のように、相関関係と因果関係では、言葉の意味が大きく変わってきます。私は数学的関連付けのできる事象同士の関係を相関関係、生物学的関連付けのできる事象同士の関係を因果関係と考えています。
どういうことかというと、相関関係の場合は、二つの事象AとBにおいてそれぞれが示している数字の大きさや動きがただただ連動している関係を言います。すなわち、相関関係の示された事象が生物学的な意味合いを持つかと言われると、それは完全に別物である、ということです。もっと乱暴な言い方にするなら、「ただ数字が動いているだけ」です。
一方、因果関係のほうは、文字通り両者(AとB)に原因と結果を明確に示す生物学的な事象が見られたこと、すなわち「これまでの生物学的な知見に基づいた考察ができる範囲内で」各々の事象のうちどちらかが原因でその結果もう片方の事象が発生したと判断できる補助データが必要なのです。
有意差の概念
その意味で、よく研究に用いられる単語「有意差」
これは、読んで字のごとく「意味のある差」であり「偶然ではない」と言える差を示す統計の概念ですが、そもそもこれには大きな誤解があるのです。
というのも、自然界における誤差、それ以外の意味のある差は明確に区別の付けられるものではありません。なぜかというと、地震や竜巻などの天災にしろ、空気汚染やバイオハザードなどの公害にしろ、それらが引き起こされる物理的な条件がおおむね異なってしまっているためです。
例えば、雪国は通常の国に比べて雪害が多いことは当たり前ですし、一方で、雪の全く降らない地域で豪雪があった場合は文句なしの異常気象認定ですよね?
このように、すべての条件をフラットにして考えることなど不可能。多数の条件の違いを一気に比較することは、科学的な考え方であるとは言えません。
ゆえに、我々は研究において実験条件を設定し、対照実験による「一部の条件を変えたことによる変化」の「統計学的相関関係を調べる」ことで因果関係を推測しているにすぎません。
そして、そこに同じ条件で違う実験者による再現(ある意味これも対照実験と言えなくもない)の数が積み重なって、定説になっていくのです。
話がそれましたが、要は、「有意差の検証は、厳密な実験条件を設定していることが前提」ということなのです。先ほど申し上げた因果関係を証明するための補助データとは、この条件を指しています。
では、実際の研究において統計はどう扱われているのか?
では、実際の研究における統計の利用について、皆様に解説をしようかと思います。
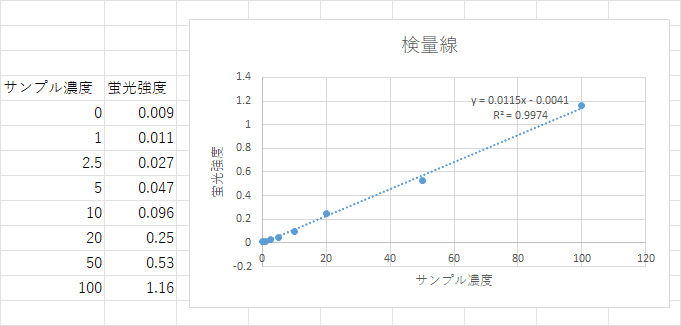
こちらの図は、私が適当に数値を充てて実験データっぽく作った検量線と呼ばれるものです。
これは、タンパク質の濃度測定をモデルにしています。
つまり、実際に何かをサンプルを測定した結果ではありません。
しかし、実際に実験をやってある程度うまくいけば、このようにサンプルの濃度と蛍光強度はきれいに比例し、直線状に並ぶことになります。
しかし、だからと言ってすべてが完全に線上かというと、そうでもないですよね?
どちらかというとわずかに上や下にずれていますよね?
そう、実際には理論値のようにきれいにはいかないのです。しかし、ある程度直線になるようなグラフになるので、一番「それっぽい」直線を引くことで濃度の分からないサンプルの蛍光強度から、濃度を求めることができます。
では、その「それっぽい直線」はどうやって求めるのでしょうか。
下の図をご覧ください。

これは、一般的なデータグラフの拡大版です。
本来この破線上に乗っていなければならない各点がそれぞれ微妙に破線からずれていることが分かります。
これは、実際の化学現象には誤差があるため、わずかに予測される直線からずれてしまうためです。
この時、各点から最も近いであろう直線にプロットの位置を修正する統計的手法があります。これを最小二乗法と言います。興味のある方は、「最小二乗法」で調べてみてください。
最小二乗法によって作成されたこの直線を近似直線と言い、この直線が分かれば、中学の数学よろしく、「yの値が分かるからxの値もわかる」ということで、蛍光強度(yの値)を直線の式に代入すれば濃度(xの値)が分かるという寸法です。
いや、ムズすぎ(笑)
すみません。自己満足で解説してしまいました。
しかし、なにも難しい話をしようというわけではなくて、要は「理論的に求められている法則も、実際にはエラーで外れることがあるからそれを補正してやろう」というときに使うもの。
それが統計学である、ということなのです。
つまり、統計学単体で示された事実は、そのまま生命現象や物理現象の再現性を保証するわけではないのです。
ではなぜ、最小二乗法のような使い方ができるかというと、統計とは独立した理論が存在するためです。
基本的にタンパク質と試薬が反応したことで発される蛍光の強さとタンパク質の濃度は比例することが科学的に分かっています。この話は、どちらかというと数学ではなく理科の化学における理論です。統計とは別の概念であるということですね。
つまり、「濃度と蛍光強度が比例する」という話は「タンパク質が濃くなればそれだけ反応も強くなる」という科学的知見をもとにして言っているため、あくまでも最小二乗法のような統計は「その反応の強さ(蛍光)は比例するはずだから、補正できるよね」としているだけです。
これは、教科書に書かれているレベルの話です。
さっきの私が適当に作ったデータの図にも、「R^2 = 0.9974」とありますが、これも統計学では「相関係数」と呼ばれる数値で、どれだけ直線にデータが近いかを表している値になります。
具体的には1に近いほど直線に近いです。
つまり、このデータはかなり精確な検量線である、ということになりますね。
つまり、無秩序な統計的手法は因果関係を示さない
この例からもわかるように、統計的手法はAとBの関係性を「なんかようわからんけど、数字は連動してるなあ……これ関係あんじゃね?」と推測する程度の信頼性を示すだけです。
だから、一つ条件が異なればこの「関連性」は途端に吹き飛びます。
先ほどのタンパクの例であれば、反応液の中に変なものが混ざったことで色が薄まって、直線にならないこともあります。
それくらいしっかりと条件を定めないといけないのです。
さて。ここまで話せばこの記事で私が言いたいことも自ずとご理解いただけるのではないかと思います。
・・・そうです。ワクチンです。
ワクチンを接種したことによる安全性リスク評価の研究モデルは複数種あります。しかし、mRNAワクチンに関しては、その多くが「統計学的有意差と2者のデータ比較による相関関係の検証」をモデルとしています。
先ほども申し上げた通り、有意差と相関関係についてはあくまでも「厳密な条件設定を前提とした」数学的な法則性に因果関係を見出すことに科学的意義があります。
しかし、mRNAワクチンにおいては、その生理活性(実際に体の中でどのようにはたらくのか、その機序)が不透明な部分が多く、想定されていなかった毒性の存在(LNPによる炎症をベースとした副作用の話、詳しくは私の「裸のmRNA」を参照ください)も少なくない数が報告されています。
つまり、従来型ワクチンに見られる典型とは違う、これまでにない作用機序による「大前提の相違」がmRNAワクチンに存在する中で、その前提による厳密な条件設定が一切合切無視されているということなのです。
具体的には「細胞の中でmRNAによる遺伝子発現でタンパクを大量に合成する」という今までのワクチンにはない機序の影響を過小評価しています。これを相関関係や有意差検定の悪用によって問題ないとする「無理のある事実化」が横行しています。
もっとざっくばらんな表現をするなら、統計による相関関係や有意差が確認されるのであれば、その研究モデルがガバガバなものであっても、それを事実として解釈しようとする傾向が、mRNAワクチン開発研究で多くみられるということです。
まさしく「統計学の悪用」
長々と語りましたが、現状、以上のような統計を利用した無理な事実化が横行しています。
そして、それが実際に世の中で起こっている科学的現象との大きな乖離を生んでいます。
「なんでワクチンが効いているはずなのに、感染者が増えるんだろう?」とか、「ワクチンが重症化予防に一役買っているのなら、なんで隠れコロナ死や超過死亡、コロナ後遺症などの影響が増長しているのだろうか?」と疑問が残ってしまうのは、ワクチンの効果や安全性を保障する統計学的な解析モデルの多くが大きな間違いをはらんでいるためです。
だから、科学現象との明確な乖離を生んでしまう。現実と想定でこれだけの差が出てしまうのです。
しかし、おおよそ研究の世界に接していない方は、その違和感を感じるだけの機会を得ることができません。未来で起こることが誰にも予測できないのと同じで、「統計で予測された、検証された」と聞けば、「それなら確かなものなんだろう」という漠然とした理解で飲み込むしかないためです。
ですので、あえて再三ではありますが、私はもう一度、申し上げます。
「今、統計は悪用されており、条件検討もされていない状態で、ワクチンの安全性研究がなされている」
以上になります。
