
三角形を通る線2本の交点の内分比の公式
今回は中学~高校数学ⅠAくらいまでで使える公式の紹介です。(前回の記事で書こうと思っていたものですがさすがに導出や説明が長すぎて分けることにしました)
公式の内容
公式は以下の図において成立するものになります。

△ABCにおいて、AB上にP,BC上にQ,CA上にRをとり、AQとPRの交点をMとする。
$$
上図において、\\
\dfrac{QM}{AM}=\dfrac{QC}{BC}(\dfrac{BP}{AP}-\dfrac{CR}{AR})+\dfrac{CR}{AR}\\
\\
また、同じことだが\\
AM:QM=1:\dfrac{QC}{BC}(\dfrac{BP}{AP}-\dfrac{CR}{AR})+\dfrac{CR}{AR}
$$
ちょっと複雑な式に見えますが、よく図と照らし合わせてみると意外と単純です。
導出① 使用する定理
今回の公式の導出には高校数学で習うであろうメネラウスの定理を使います。定理自体はものすごく簡単なものです。
(1) 定理の内容
メネラウスの定理とは、主に下図において成り立つ定理です。
三角形の辺の延長線上と三角形の頂点を通らない直線です。

$$
\dfrac{PB}{AP}\times\dfrac{RC}{BR}\times\dfrac{QA}{CQ}=1
$$
これは下のように直線が三角形の外部にある場合も成立します。

(2) 定理の証明
ここでは正確な証明は省略し、方針だけ書いておきます。
直線PQに平行な線を3本引きます(A,B,Cを通します)。

$${上図において、平行線と比の性質から\\BR:RC=BP:PD, CQ:QA=DP:PA\\したがって、\dfrac{RC}{BR}=\dfrac{PD}{BP}, \dfrac{QA}{CQ}=\dfrac{PA}{DP}}$$
ここから$${\dfrac{PB}{AP}}$$との掛け算をして、右辺がすべて約分されて1になることから導出されます。
導出② 補助線を引いて三角形を作る
ここからいよいよ導出です。
メネラウスの定理が分かれば中学生でも余裕で理解できるものです。
(1) 延長線を引く
まずは先ほどのメネラウスの定理が使えるように下のような感じで補助線を引きます。
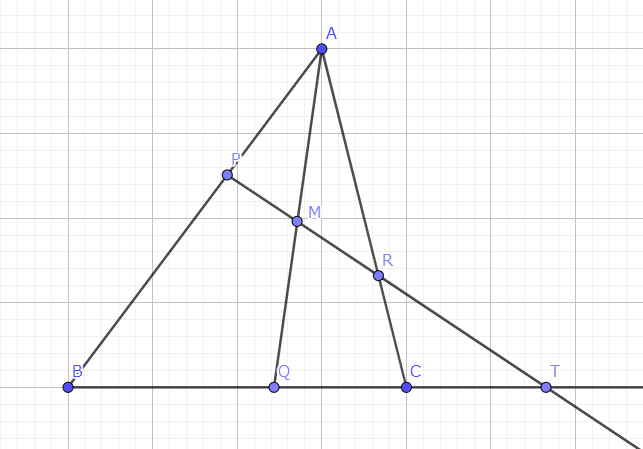
補助線はよくありそうな感じですね。一応言葉で説明すると下のようになります。
$${辺BCをCの方向に延長した半直線BCと、\\線分PRをRの方向に延長した半直線PRとの交点をTとする。}$$
(2) 延長線と三角形、交差する直線
先ほどの図をもう一度見てみましょう。この図にはメネラウスの定理が使えそうな三角形と直線の組がたくさんあることが分かります。

今回はそのうち2つに着目して公式を導出していきます。
導出③ 式変形
(1) △ABCと直線PTに着目してTCを求める
まずは$${\triangle ABC}$$に着目します。
$${△ABCにおいて、メネラウスの定理より、\dfrac{TC}{BT}\cdot\dfrac{AR}{CR}\cdot\dfrac{BP}{AP}=1\\これをTCについて解くと、TC=\dfrac{BT\cdot CR\cdot AP}{AR\cdot BP}\\BT=BC+TCより、TC=\dfrac{BC\cdot CR\cdot AP}{AR\cdot BP}+\dfrac{TC\cdot CR\cdot AP}{AR\cdot BP}\\再度TCについて解くと、TC=\dfrac{CR\cdot AP\cdot BC}{AR\cdot BP-CR\cdot AP}}$$
(2) △AQCと直線MTに着目してQM/AMを求める
今回求めるのは$${\dfrac{QM}{AM}}$$なので、とりあえず補助線によってできた$${T}$$を使ってもよいのでそれぞれの値で表していきます。今回の場合は先ほど求めた$${TC}$$を使って表していくのが目標です。
$${△AQCにおいて、メネラウスの定理より、\dfrac{QM}{AM}\cdot\dfrac{TC}{QT}\cdot\dfrac{RA}{CR}=1\\これを変形して、\dfrac{QM}{AM}=\dfrac{QC\cdot CR+TC\cdot CR}{TC\cdot RA}=\dfrac{QC\cdot CR}{TC\cdot RA}+\dfrac{CR}{RA}}$$
導出④ 代入してひたすら計算
(1) 代入
かなり面倒ですが、さきほどの$${\dfrac{QM}{AM}}$$の式に$${TC}$$の式を代入していきます。
$${\dfrac{QM}{AM}=\dfrac{QC\cdot CR}{TC\cdot RA}+\dfrac{CR}{RA}\\TC=\dfrac{CR\cdot AP\cdot BC}{AR\cdot BP-CR\cdot AP}より、\\\dfrac{QC\cdot CR}{TC\cdot RA}+\dfrac{CR}{RA}\\=\dfrac{QC\cdot CR}{\frac{CR\cdot AP\cdot BC\cdot RA}{AR\cdot BP-CR\cdot AP}}+\dfrac{CR}{RA}\\=\dfrac{QC\cdot CR\cdot ({AR\cdot BP-CR\cdot AP})}{CR\cdot AP\cdot BC\cdot RA}+\dfrac{CR}{RA}\\=\dfrac{QC\cdot CR\cdot AR\cdot BP}{CR\cdot AP\cdot BC\cdot RA}-\dfrac{QC\cdot CR\cdot CR\cdot AP}{CR\cdot AP\cdot BC\cdot RA}+\dfrac{CR}{RA}\\=\dfrac{QC\cdot BP}{BC\cdot AP}-\dfrac{QC\cdot CR}{BC\cdot AR}+\dfrac{CR}{RA}}$$
最終的には約分されて割ときれいになりますが、途中はものすごく面倒です。
(2) 代入後の2通りの整理方法
最後に$${\dfrac{QC\cdot BP}{BC\cdot AP}-\dfrac{QC\cdot CR}{BC\cdot AR}+\dfrac{CR}{RA}}$$を整理します。2通りのくくりかたがあるので、それを書いておきます。
$${① \dfrac{QM}{AM}=\dfrac{QC}{BC}(\dfrac{BP}{AP}-\dfrac{CR}{AR})+\dfrac{CR}{AR}\\ \\② \dfrac{QM}{AM}=\dfrac{QC\cdot BP}{BC\cdot AP}-\dfrac{CR}{AR}(\dfrac{QC}{BC}-1)}$$
【補足】直線PRの傾きが逆の場合
今回は直線PRの傾きが右下がりですが、右上がりの場合はABとの交点はABの延長線上のBではなくAのほうにあります。このときも、交点をTとおくとメネラウスの定理より導出に使った2つの式を得ることができるので、直線PRの傾き方は公式には関係がないとわかります。
練習問題
最後にこの公式を使う練習問題を1つ。
$${△ABCにおいて、辺AB上に点P、辺BC上にQ、辺AC上にRをとる。\\PとR、AとQを結び、PRとAQの交点をMとする。\\AP:PB=1:2,BQ:QC=3:5,AR:RC=3:2のとき、\\AM:QMの値を求めなさい。}$$
↓↓↓解答・解説↓↓↓
解答・解説
問題文の文字は今回の場合は公式通りなので、そのまま代入して大丈夫ですが、$${BQ:QC=3:5}$$だけ注意しましょう。公式はBCとQCを使うので、BQ:QCではなく、BC:QCにする必要がありますね。$${BQ:QC=3:5}$$より、$${BC:QC=(BQ+QC):QC=(3+5):5=8:5}$$です。
これを公式に代入すると、$${\dfrac{5}{8}(\dfrac{2}{1}-\dfrac{2}{3})+\dfrac{2}{3}=\dfrac{3}{2}}$$
したがって、$${AM:QM=2:3}$$
このように、本来は相似などを使って解く問題をすぐに簡単に解くことができます。ぜひ覚えて使ってみてください!
