
関数描画ソフトGeoGebraで原子のモデル図を作る
関数描画ソフトのGeoGebra(https://www.geogebra.org/calculator)。いろいろなことができますが、今回は原子のモデル図を作る方法を紹介します。
完成図としては下のようになります。
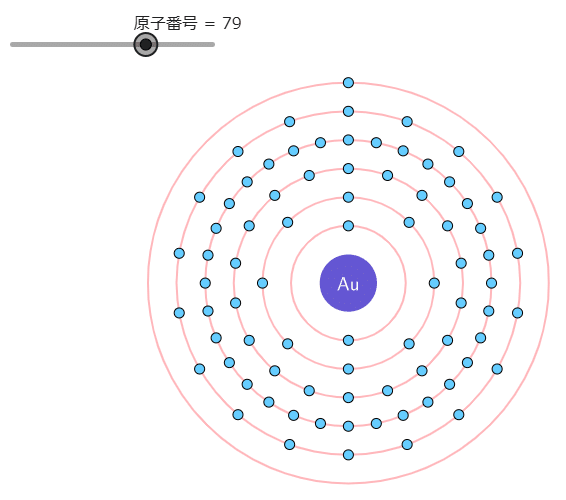
1. 原子に関する基礎知識
まずは軽く作成に必要な知識を書いておきます。
(1) 原子の構造
原子は、基本的には大雑把に言うと陽子、中性子、電子からなります。また、陽子と中性子をまとめて原子核ともいいます。水素以外の原子(イオン、同位体を除く)は陽子、中性子、電子の数はすべて原子番号に等しくなります(水素原子は中性子がなく、陽子と電子が1つずつ)。例えば、原子番号17の塩素(Cl)は陽子17個、中性子17個、電子17個、原子番号100のフェルミウム(Fm)は陽子100個、中性子100個、電子100個といった感じです。そして、原子核は原子の中心に位置し、電子はその周りを軌道に乗って回っているような感じになっています(正確には電子は確率の雲として存在していますがここではややこしくなるので省略します)。一般に、この軌道を電子軌道、電子の配置を電子配置と言ったりします。
(2) 電子軌道、電子配置
電子軌道ですが、こちらにはいくつか種類があり、現在発見されている118番までの範囲ではs,d,f,pの4種類です。また、それぞれの前に数字を付けて1s,2s,3p,3d,…などと表します。この数字が同じものはモデル図では同じところに入るとして書かれます。例えば、4s,4f,4d,4pはモデル図ではすべて同じ円上に電子を配置するように書きます。ここでは各元素の詳しい電子配置などは省略しますが、だいたい内側から埋まっていくという規則性があります。また、この数字の軌道を内側からK殻、L殻、M殻、…と表したりします。(現在は7pまであるのでQ殻まであります。)
2. 使うGeoGebraの基本関数
ここではすべての関数を紹介するわけではありませんが、リストに関する基本関数を紹介しておきます。(若干プログラミング要素が入ります)
(1) Element関数
まずはリストから何番目の値を取り出すかを指定する$${\verb|Element|}$$です。この関数の構文は次のようになります。
Element(リスト, 取り出す要素が左から何個目か)例えば、リスト$${\verb|a={0,1,2,3}|}$$と定義したとき、$${\verb|Element(a,2)|}$$を入力すると$${\verb|a|}$$の左から2番目の要素である$${\verb|1|}$$が出力されます。
(2) Sequence関数
次に$${\verb|Sequence|}$$です。これは初項1,公比1で指定した数までの等差数列をリストとして出力する関数です。構文は次のようになります。
Sequence(指定する数)例えば、$${\verb|Sequence(5)|}$$とすると、初項1、公比1の等比数列を5までリストにした$${\verb|{1,2,3,4,5}|}$$が出力されます。
(3) Flatten関数
これはリストを名前の通り”Flat”にする関数です。構文より先に例を見たほうが早いと思います。例えば、$${\verb|Flatten({1,2,{3,4},{5,{6,7}}})|}$$のようにリストの中にリストが入ったりしている複雑な形を$${\verb|Flatten|}$$に入れると、$${\verb|{1,2,3,4,5,6,7}|}$$ときれいに1つのリストにまとめられます。構文は次のようになります。
Flatten(整理したいリスト)(4) Take関数
これは$${\verb|Element|}$$関数のエリア指定バージョンのようなものです。構文は以下のようになります。
Take(リスト, 取り出すエリアの最初, 取り出すエリアの最後)例えば、$${\verb|a={0,1,2,3,4,5}|}$$として、$${\verb|Take(a,2,5)|}$$と入力すると、$${\verb|a|}$$の左から2番目の要素から左から5番目の要素の間をすべて取り出し、$${\verb|{1,2,3,4}|}$$が出力されます。
(5) Text関数
これは指定したテキストを指定した場所に書いてくれる関数です。構文は以下のようになります。(構文は色々ありますが一番指定しやすいものを紹介します)
Text(書くテキスト,書く座標,変数代入するか,LaTeX形式にするか,水平方向配置,垂直方向配置)座標は$${\verb|(0,0)|}$$のような書き方で、変数代入とLaTeXに関しては真偽値($${\verb|true/false|}$$)、水平方向配置と垂直方向配置は$${\verb|-1,0,1|}$$のいずれかの値を入れます。水平方向と垂直方向の配置の値に対応する配置は次のようになります。
$${\verb|-1:水平方向に左へシフト/垂直方向に下へシフト|\\\verb|0:水平方向/垂直方向に中央揃え|\\\verb|1:水平方向に右へシフト/垂直方向に上へシフト|}$$
変数代入に関しては書くテキストの中に変数が含まれる場合に変数の値を代入して書くか($${\verb|true|}$$)、変数名をそのまま書くか($${\verb|false|}$$)という値です。
3. 原子核と電子軌道の円を作る
いよいよGeoGebraを使って作っていきます。
(1) 原子核
こちらは簡単で、半径1の円の内側を塗りつぶすだけです。つまり、$${x^2+y^2<1}$$という式になります。入力したら式の右側にある︙マークをクリック→設定 と押して色や線などの調整をします。下のような画面が出ればOKです。
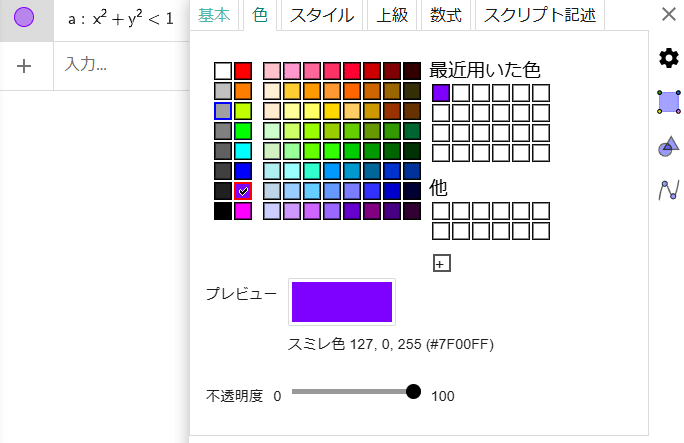
入力して設定画面を閉じると下のように円が表示されているはずです。ここで注意点ですが、もし$${a:x^2+y^2<1}$$になっている場合は下のように$${b:x^2+y^2<1}$$に変更しておいてください。(変更しないと後で少し面倒なことになります)
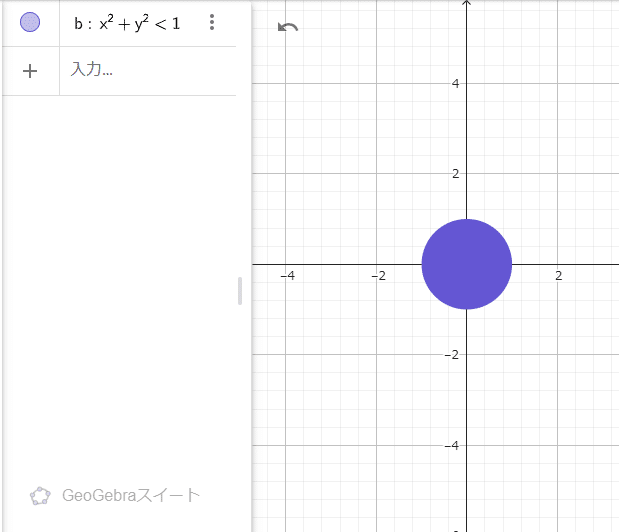
(2) スライダーを作る
次に、下のように入力してスライダーを作ります。

そして、-5と書かれているところをクリックして下のように入力します。

Enterキーなどを押すとスライダーの上限の値が変わり、左側にある〇をクリックすると下のようにグラフにスライダーが表示されるはずです。

こちらも設定を開いて、「a=」ではなく「原子番号=」にラベルを変えてもいいと思います。

参考にどうぞ。
(3) 軌道のリストと軌道の描画
軌道の数は基本的に周期表における周期の値の数に等しくなります。例えば、カルシウム(Ca)は第4周期なので軌道は4つです。このことを参考にリストを作ります。下の構文を入力します。コピペで大丈夫です。
Z=Flatten({1,1,2*((Sequence(8))/(Sequence(8))),3*((Sequence(8))/(Sequence(8))),4*((Sequence(18))/(Sequence(18))),5*((Sequence(18))/(Sequence(18))),6*((Sequence(32))/(Sequence(32))),7*((Sequence(32))/(Sequence(32)))})これはかなり強引な方法で、$${\verb|2*((Sequence(8))/(Sequence(8))|}$$は2を8個作りたいがために約分で打ち消して2を掛けています。8個というのは第2周期の元素が8個であることからです。他も同様です。こちらのリストは$${\verb|a|}$$番目の値が何個の軌道かどうかを表しています。
次に、軌道の半径を変数として作っておきます。下の構文を入力してください。
r=Unique(Take(Z,1,a))+1$${\verb|Unique|}$$関数は引数のリストの重複する要素を削除して、かつ昇順に並べ替える関数です。中身の$${\verb|Take|}$$関数は軌道の円が複数個できるのでその半径をすべて取り出すということをしています。最後の$${\verb|+1|}$$は半径1から始めてしまうと原子核に重なってしまうのでそれを避け、1個目の軌道を半径2にするためです。
最後に円を作ります。これが構文は一番単純です。
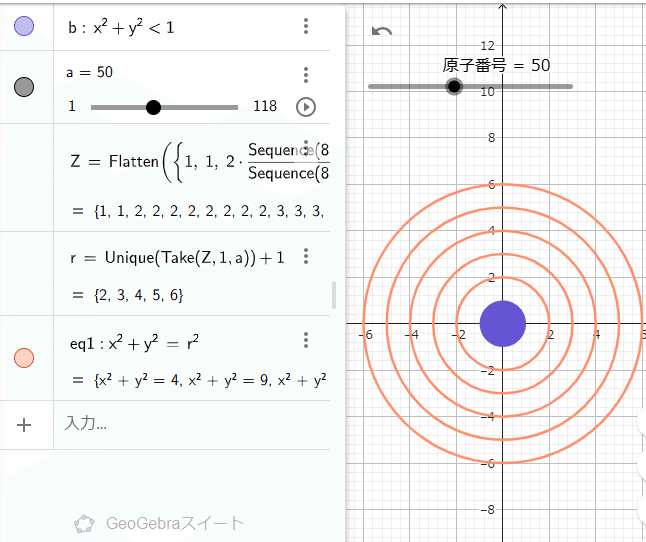
x^(2)+y^(2)=r^(2)これを入力すると下のようになるはずです。

ここまでできたらスライダーを動かしてみましょう。軌道の円が増えたり減ったりするはずです。
4. 電子の配置の前に ~円周のn等分点~
さて、次に電子の配置に入っていくのですが、ここからは一気に構文が複雑になるので、その前に電子配置がどのような座標になるかを紹介しておきます。
(1) 電子の軌道上の配置
電子は、モデル図では基本的に軌道をきれいに等分した点におかれます。軌道上の電子の数が奇数の場合は、そのまま等分する点と1つ足した数で等分して左上だけ欠けた状態にするという2つのパターンがありますが、イオンになりやすいという不安定さを表現するためにも今回は後者を選びます。(前者の場合も後で作るときに少し紹介します)
(2) 円周上のn等分点の座標
どこを基準点(n=1のときの点)とするかで式は変わりますが、今回は$${(0,r)}$$を基準点とします。(一般的な基準点は$${(r,0)}$$です)
結論から言うと座標は次のようになります。
$$
半径rの円のn等分点のk番目の座標は、\\
(-r\sin(\frac{2\pi k}{n}),r\cos(\frac{2\pi k}{n}))
$$
一応導出を書いておきます。
$${半径 r の円周上の点の座標を極座標で表すと、\\(r\cos\theta,r\sin\theta)\\ここで、円周を n 等分することを考えると、\\円周は2\pi_{(RAD)}であるので、角度は\dfrac{2\pi}{n}ずつずれる。\\したがって、k番目は\theta=\dfrac{2\pi k}{n}で表されるので、座標は、\\(r\cos\dfrac{2\pi k}{n},r\sin\dfrac{2\pi k}{n})\\しかし、これでは基準点(k=0)のとき(r,0)になるので、\\これを反時計回りに\dfrac{\pi}{2} {}_{(RAD)}回転させると、\\(-r\sin(\dfrac{2\pi k}{n}),r\cos(\dfrac{2\pi k}{n}))}$$
(3) 奇数の"欠けた"表現方法
軌道に入る電子が奇数のときの欠けた表現とは、具体的には下のようになります。

ここで、一番内側のK殻にある2つの電子は全く関係ないので、その次のM殻に入る7個の電子を考えればよいです。ここで、次の元素のネオン(Ne)を見てみましょう。

M殻の電子の形はF、Neともに左上があるかないかの違いだけです。つまり、奇数の場合は電子の配置は+1した偶数の値(7の場合は8)の配置にしただけです。式は次のように変更されます。
$$
(-r\sin(\dfrac{\pi k}{\lceil \frac{k}{2}\rceil}),r\cos(\dfrac{\pi k}{\lceil \frac{k}{2}\rceil}))
$$
$${\lceil x\rceil}$$は$${ x }$$を整数に切り上げすることを意味します。これの導出は省略しますが、基本的に分母分子を2で割るだけです。
5. 電子を配置する
次に配置ですが、基本的に配置用のリストを作って配置用の構文をコピーするだけです。
(1) K殻
まずはK殻からやっていきます。K殻の配置用のリスト構文は下のようになります。
k=Flatten({1,2*((Sequence(117))/(Sequence(117)))})配置用の関数構文は下のようになります。
K=(-Element(r,1) sin(((π (Sequence(Element(k,a))+1))/(ceil(((Element(k,a))/(2)))))),Element(r,1) cos(((π (Sequence(Element(k,a))+1))/(ceil(((Element(k,a))/(2)))))))この2つを入れると下のようになります。
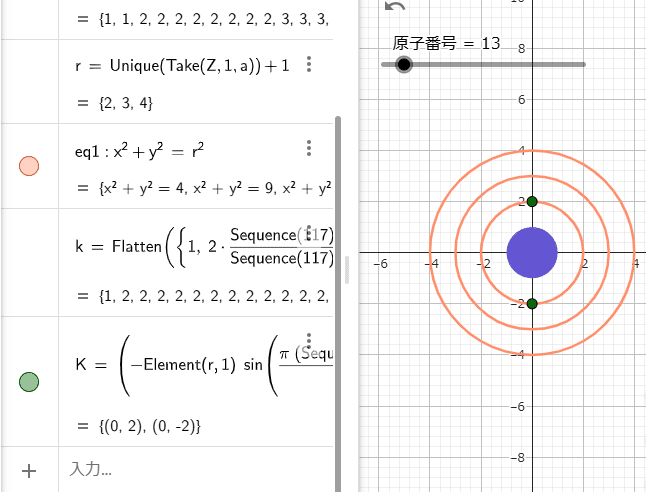
$${\verb|Element(r,1)|}$$は円の半径を表し、$${\frac{\verb|Element(k,a)|}{\verb|2|}}$$は等分する数を表します。分子の$${\verb|Sequence(Element(k,a))|}$$は変数の値をすべてまとめたもので、最後の$${\verb|+1|}$$は空白位置の調整用です。
(2) L殻
次にL殻ですが、配置用のリスト構文を変え、また関数の構文の半径と変数をいじるだけです。
l=Flatten({0,0,1,2,3,4,5,6,7,8*((Sequence(109))/(Sequence(109)))})L=(-Element(r,2) sin(((π (Sequence(Element(l,a))+1))/(ceil(((Element(l,a))/(2)))))),Element(r,2) cos(((π (Sequence(Element(l,a))+1))/(ceil(((Element(l,a))/(2)))))))これを入力すると次のようになります。
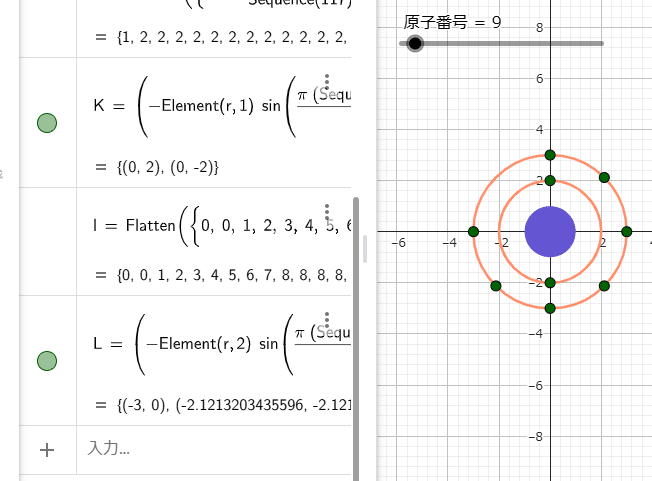
(3) M殻以降
M殻以降も、L殻と同様にコピーをしていくだけです。
まずは配置用のリストの構文一覧です。
m=Flatten({0*((Sequence(10))/(Sequence(10))),1,2,3,4,5,6,7,8,8,8,9,10,11,13,13,14,15,16,18*((Sequence(90))/(Sequence(90)))})n=Flatten({0*((Sequence(18))/(Sequence(18))),1,2,2,2,2,1,2,2,2,2,1,2,3,4,5,6,7,8,8,8,9,10,12,13,13,15,16,18*((Sequence(12))/(Sequence(12))),19,21,22,23,24,25,25,27,28,29,30,31,32*((Sequence(49))/(Sequence(49)))})o=Flatten({0*((Sequence(36))/(Sequence(36))),1,2,2,2,1,1,2,1,1,0,1,2,3,4,5,6,7,8,8,8,9,9,8,8,8,8,8,9,8,8,8,8,8,8,9,10,11,12,13,14,15,17,18*((Sequence(12))/(Sequence(12))),20,21,22,24,25,25,27,28,29,30,31,32*((Sequence(17))/(Sequence(17)))})p=Flatten({0*((Sequence(54))/(Sequence(54))),1,2*((Sequence(22))/(Sequence(22))),1,1,2,3,4,5,6,7,8,8,8,9,10,9,9,9,8,8,9,8,8,8,8,8,8,9,10,11,12,13,14,15,16,18*((Sequence(8))/(Sequence(8)))})q=Flatten({0*((Sequence(86))/(Sequence(86))),1,2*((Sequence(23))/(Sequence(23))),1,2,3,4,5,6,7,8})次に配置用の関数の構文です。
M=(-Element(r,3) sin(((π (Sequence(Element(m,a))+1))/(ceil(((Element(m,a))/(2)))))),Element(r,3) cos(((π (Sequence(Element(m,a))+1))/(ceil(((Element(m,a))/(2)))))))N=(-Element(r,4) sin(((π (Sequence(Element(n,a))+1))/(ceil(((Element(n,a))/(2)))))),Element(r,4) cos(((π (Sequence(Element(n,a))+1))/(ceil(((Element(n,a))/(2)))))))O=(-Element(r,5) sin(((π (Sequence(Element(o,a))+1))/(ceil(((Element(o,a))/(2)))))),Element(r,5) cos(((π (Sequence(Element(o,a))+1))/(ceil(((Element(o,a))/(2)))))))P=(-Element(r,6) sin(((π (Sequence(Element(p,a))+1))/(ceil(((Element(p,a))/(2)))))),Element(r,6) cos(((π (Sequence(Element(p,a))+1))/(ceil(((Element(p,a))/(2)))))))Q=(-Element(r,7) sin(((π (Sequence(Element(q,a))+1))/(ceil(((Element(q,a))/(2)))))),Element(r,7) cos(((π (Sequence(Element(q,a))+1))/(ceil(((Element(q,a))/(2)))))))これを入力すれば基本は完成になります。スライダーを動かすとモデル図も変わるはずです。
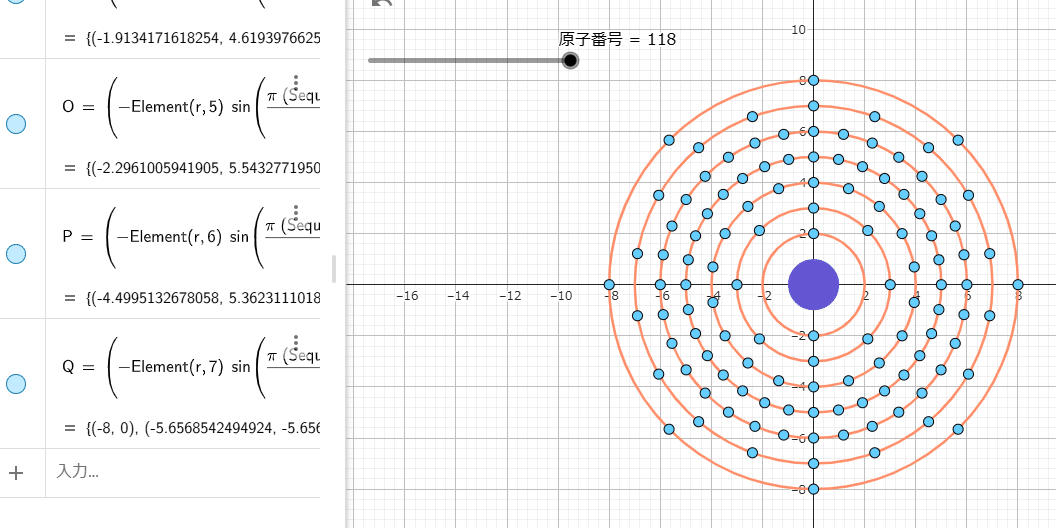
6. 元素記号を書く
次に原子核の中央に元素記号を書いていきます。
まずは元素記号のリストを定義します。
name1={"H","He","Li","Be","B","C","N","O","F","Ne","Na","Mg","Al","Si","P","S","Cl","Ar","K","Ca","Sc","Ti","V","Cr","Mn","Fe","Co","Ni","Cu","Zn","Ga","Ge","As","Se","Br","Kr","Rb","Sr","Y","Zr","Nb","Mo","Tc","Ru","Rh","Pd","Ag","Cd","In","Sn","Sb","Te","I","Xe","Cs","Ba","La","Ce","Pr","Nd","Pm","Sm","Eu","Gd","Tb","Dy","Ho","Er","Tm","Yb","Lu","Hf","Ta","W","Re","Os","Ir","Pt","Au","Hg","Tl","Pb","Bi","Po","At","Rn","Fr","Ra","Ac","Th","Pa","U","Np","Pu","Am","Cm","Bk","Cf","Es","Fm","Md","No","Lr","Rf","Db","Sg","Bh","Hs","Mt","Ds","Rg","Cn","Nh","Fl","Mc","Lv","Ts","Og"}ただひたすらに元素記号を並べただけのリストです。
次にテキストをグラフ上に描画する構文です。
text1=Text(Element(name1,a),(0,0),true,true,0,0)$${\verb|Text|}$$関数を利用して$${\verb|(0,0)|}$$に中央揃えで番号に対応する記号を書いています。この2つを入力すると次のようになるはずです。
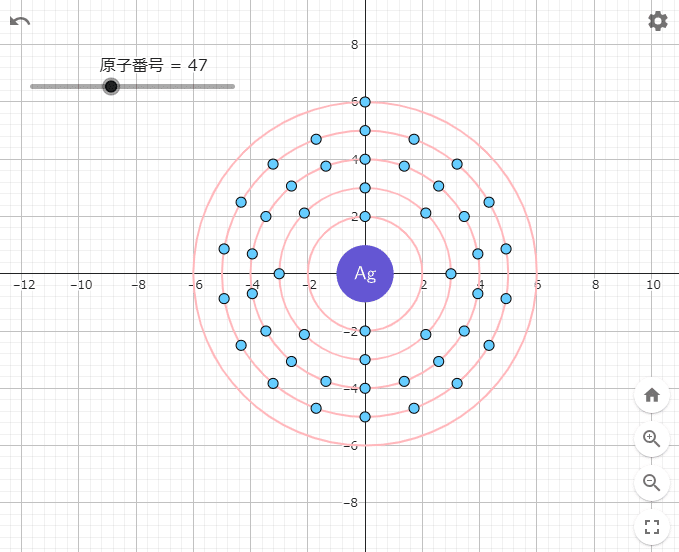
最後に右上の設定から「軸を表示」をOFFにしてグリッドを「グリッドなし」にします。
これでモデル図は完成です。発展として元素名などの情報を書き込んでもいいと思いますが、ここでは省略します。
