
数学が嫌いだけどできるようになりたい人が見る取扱説明書⑤
↑↑前回の続きになっています.是非ご覧ください
↑↑初めて来られた読者は最初から読むことをおすすめします.
前回は数学の勉強方法の前半部分について解説を行った.再度復習を行うと
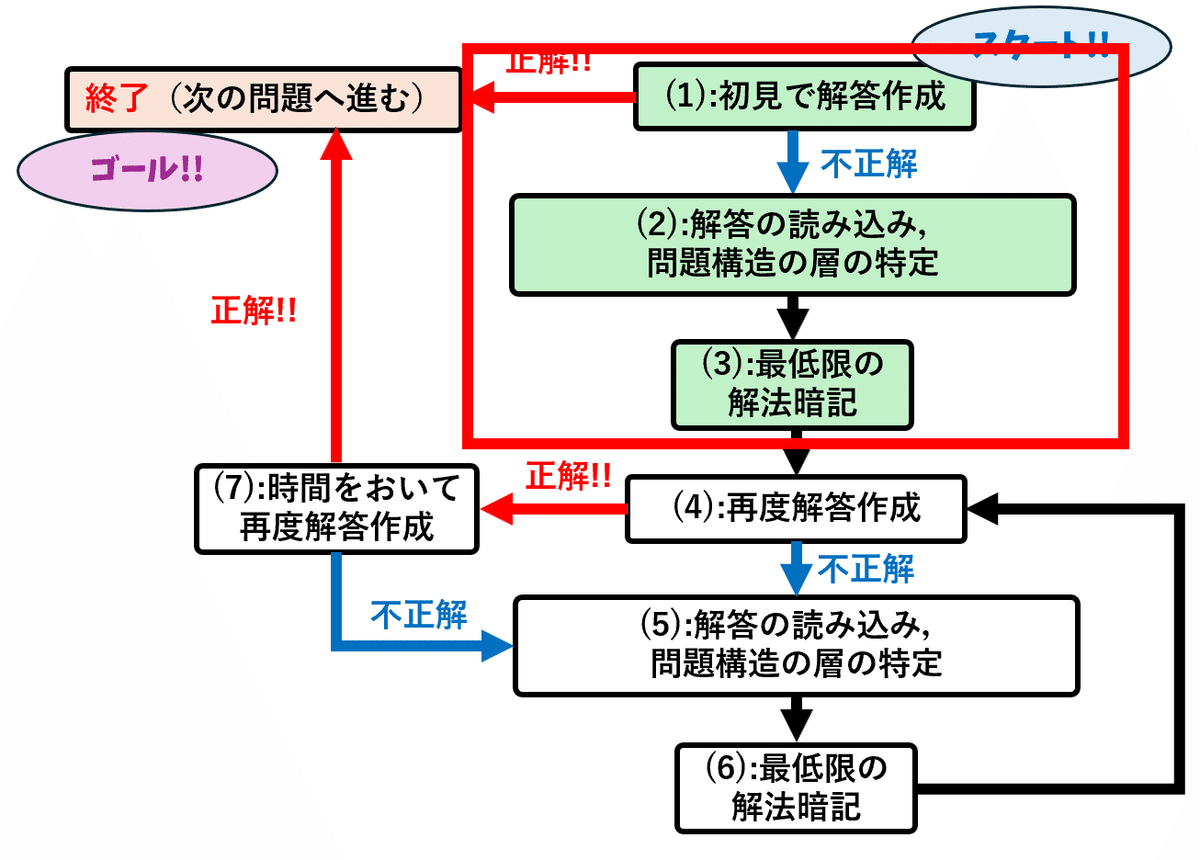
(1):まずは問題に取り掛かり,自分のできる範囲で解答を作る.解答が思いつかない場合は早い段階で諦め,スピード感を持って解答解説を熟読する.・正解の場合→終了(次の問題へ) ・不正解の場合→(2)に進む
(2):解答解説を読み込んで,自分はどの部分が思いつかなかったのか・誤解していたのかを問題構造の層として捉え,課題設定を行う.さらに未到達の問題構造の層と仕分けを行う必要もある.・完了後→(3)に進む
(3):(2)で課題設定を行った思いつかなかったり,誤解していたり,計算ミスをしてしまった問題構造の層についてのみ暗記する.決して未到達の問題構造の層については暗記してはいけない.・完了後→(4)に進む
このことを踏まえて今回は数学の勉強方法の後半部分について詳しく解説しようと思う.
1. 数学の勉強法と具体例(後半戦)
(4):再度問題にチャレンジし,できる範囲で解答作成してみる.思いつかない場合は気持ちを切り替えて解答解説を読み込む.
・正解の場合→(7)に進む ・不正解の場合→(5)に進む
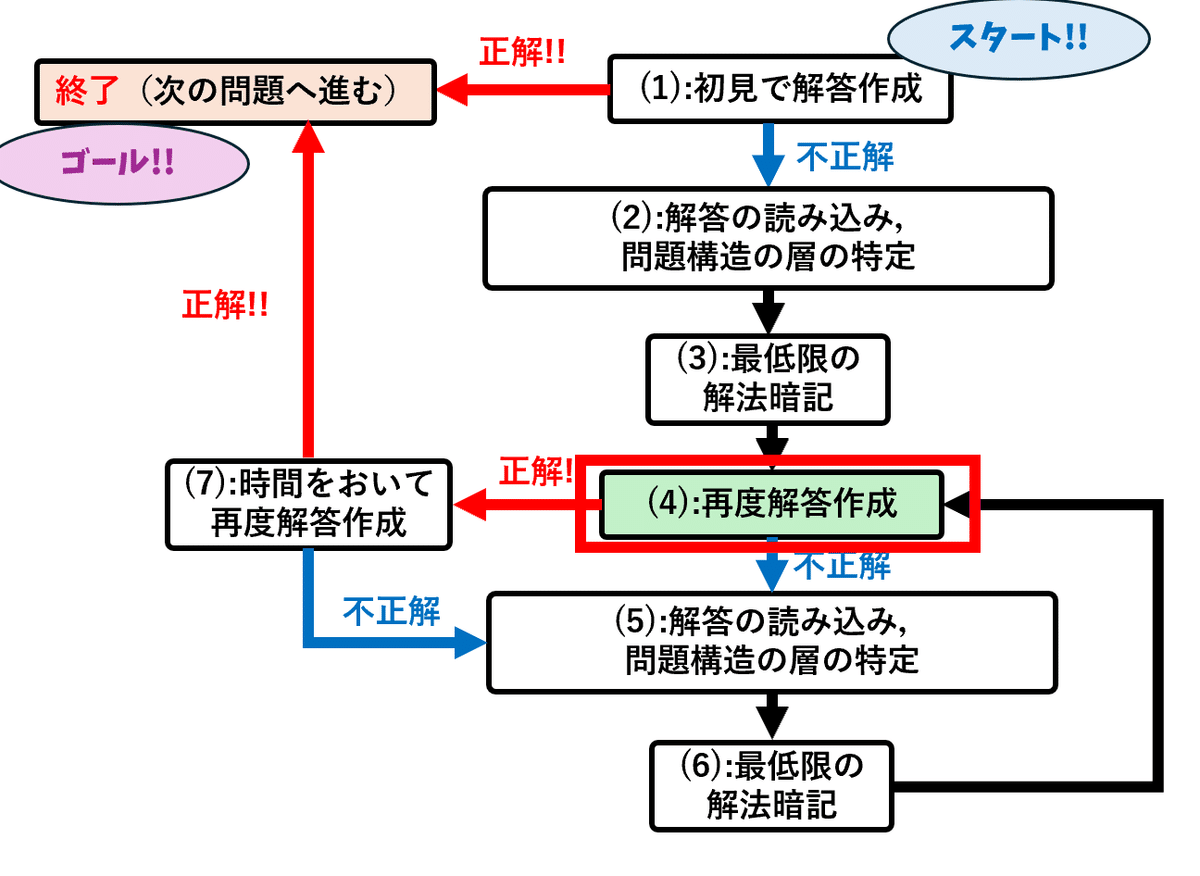
(3)にて思いつかなかったおよび誤解していた問題構造の層について課題設定を行い,解法暗記を行った.再度問題にトライし解答作成を行ってみよう.
具体的に前回解説を行った日比谷高校の数学の問題で解説を行う.
<復習>

今回は「直角二等辺三角形の二等分線と垂線の性質」および「直角二等辺三角形の二等分角と垂線の性質」について完全習得(暗記)したので筆者が再度解答を実際に作成したものを提示する.

結果,直角二等辺三角形の性質を理解していたため,点Hを2つの表現を用いて連立するフェーズまで運ぶことができた.しかしtの2乗を消去してaだけの1次方程式を解いた結果,a=-1/2 という解が得られ問題文の条件a>0 の題意に矛盾する形になってしまった.→不正解
このように解答解説を読み込んでいたとしても実際に再トライしてみると違った方向で躓いて正解にたどり着かないパターンも多い.
なぜなら初見では前半部分で躓いていた解答が解答解説を読み込みこむことで次の段階へと駒を進めることができたが,初見の段階では遭遇していなかった未到達の問題構造の層へ2回目にして初遭遇したためである.
2回目の解答作成でも初めて到達した問題構造の層は初見で解答作成するのとほとんど変わらないので,1度解答を見たからという理由で解答を習得した気持ち(慢心)でいると実体は全く数学の能力として身についていないという無駄な時間を過ごす結果になってしまう.
少々面倒くさい気持ちは分かるが数学が苦手な人こそ1つずつ,1つずつ「できない項目」や「覚えていない項目」を潰していくためにはこれしかないと思って気合を入れて頑張って欲しい.
なお (1)と同様に解答が思いつかないのであれば潔くすぐに解答作成を諦めて解答解説を読み込もう.
・正解の場合→(7)に進む ・不正解の場合→(5)に進む
(5):(2)の手順と同じ(解答解説を読み,自分が思いつかなかった・誤解していた問題構造の層を把握する.未到達の問題構造の層との仕分けも同時に行う.)
・完了後→(6)に進む

(2)の手順をもう1度行い,解答解説を読み込み,自分で思いつかなかったおよび誤解していた問題構造の層の把握と未到達の問題構造の層との仕分けを行う.
これも再度復習がてら具体例を用いて説明する.


間違い探しのようだが筆者の作成した解答と解答解説を見比べて見よう…するとACの中点Hのy座標の求め方が違うのが分かるのではなかろうか?
今回は分かりやすく赤字で色をつけているが,2回目の解答で正解できなかった理由は「2点間の中点座標の求め方」に関して誤解していたからである.筆者の解答では「2点の座標を引き算して÷2」を行っているのに対して解答解説では「2点の座標を足し算して÷2」を行っている.
誤解する原因として解答解説②を見てみるとACの中点Hまでの長さを求めており(赤字)こちらは「2点の座標を引き算して÷2」を行っている.こちらはあくまでも「2点間と中点までの長さの求め方」であって「2点間の中点座標の求め方」とは全く違うので注意が必要である.
筆者は「2点間の中点座標の求め方」と「2点間と中点の長さの求め方」についての理解が混在しており,中点座標を求める際に中点までの長さを求める計算を行っているのだ.(これはものすごく間違えやすいので皆さんも注意しよう)
さらに実際に筆者の解答プロセスのチャート図を作成した.

この例題に関してはACの中点Hの座標を求める計算を誤解していた.フローチャートでは赤枠で囲まれている部分を指す.
今回は思いつかなかったケースではなく,ある知識や解法に関して「誤解」していたため誤解していた問題構造の層は全て青い矢印が付いている.しかしaを求める段階以降は解答作成に至っていないため未到達の問題構造の層(ピンク色)が残っている.
「直角二等辺三角形の二等分線と二等分角,垂線の性質」を理解したことで問題の過程に進展を見せたことにより未到達の問題構造の数が減った.
(2)でも解説したが解答解説を読み込む際に問題構造の層を意識しながら不正解に至った原因を考えるのがよい.その時に必ず思いつかなかった・誤解していた問題構造の層と未到達の問題構造の層を分けて考えることが重要だ.
・完了後→(6)に進む
(6) (3)の手順と同じ((5)の段階で原因を特定した,思いつかなったおよび誤解していた問題構造の層だけ暗記する)
・完了後→(4)に戻る

ここでは(3)と同様に思いつかなかったおよび誤解していた問題構造の層だけ暗記する.暗記に関しては(3)と同様なので割愛させていただく.
今回の例題で言うならば,「ACの中点Hの座標の求め方」と「ACの中点Hまでの長さの求め方」について混在していたことが間違えた原因になる.
このことをちゃんと頭の中で仕分けしたうえで暗記しよう.(同じ中点について求める方法で計算式も紛らわしいので皆さんも注意)

(非常に紛らわしいので皆さんも注意してください)
・完了後→(4)に戻る
(7):(4)で正解した場合→時間をおいて再度解答作成を行う.
・正解の場合→終了(次の問題へ) ・不正解の場合→(5)に戻る

次は(4)で正解した場合は実際に暗記した箇所が自分の知識として定着しているか確認するために時間をおいて再度問題にチャレンジしよう.
どのくらい時間をおいて再度解答作成すればよいか?
だいたい授業の時間に問題を解いたのであれば家に帰った後解くのでいいし,1日時間をおいても全然構わない.同じ「時間をおく」でも人によって様々なので一概に何日とは言えないが,記憶の定着を考えると24時間以内に再トライする方が良いと思う.
それ以上時間を離してしまうとせっかく暗記した解法も抜けてしまう可能性があるからだ.問題の記憶が抜ける前にしっかり復習を行い自分の知識として会得する必要があるためおすすめは24時間以内に再トライするのが良い.
・正解の場合→終了(次の問題へ) ・不正解の場合→(5)に戻る
2.数学の勉強法についてのまとめ
一旦数学の勉強法についてのまとめに入る.勉強法の後半戦は以下のようになる.
(4):再度問題にチャレンジし,解答を作成しよう.思いつかない場合は潔く解答解説を読み込もう.・正解の場合→(7)に進む ・不正解の場合→(5)に進む
(5):解答解説を読み,思いつかなかった・誤解していた問題構造の層を特する.さらに未到達の問題構造の層と仕分ける.・完了後→(6)に進む
(6):(5)にて特定した思いつかなかった・誤解していた問題構造の層のみの解法を暗記する.・完了後→(4)に戻る
(7):(4)で正解した後,時間をおいて再度解答を作成する. 正解の場合→終了(次の問題へ) ・不正解→(5)に戻る
続いては数学の勉強法においての鉄則(アドバイス)について解説する.
3.数学の勉強法についての鉄則
その1 問題集や参考書は必ず最後までやりきる(途中であきらめてはいけない)
1つ目は問題集や参考書は最後までやりきることである.理由は以前に少しお話したが数学が得意な人と苦手な人の学習経験値の差は何事にも後半部分で顕著に表れてくるからだ.
数学が苦手な人が多く口にする「苦手な数学の単元」は中学生なら三平方の定理・立体図形や三角形の合同や相似の部分,高校生の文系なら数列・ベクトルであることは大体決まっている.
なぜならこれらの単元は共通して現在教科書の最後の単元として掲載されているからである.最後に掲載されている単元は教科書も参考書も含み皆途中で諦めてしまうため最後までしっかりやりきっている学生は案外少ないのも事実である.
これだけではない.数学はテストの問題構造上,前半から後半にかけて難易度が上がるようになっているため苦手な人は比較的序盤で躓き,得意な人は最後まで解ききってしまう.そのため数学が苦手な人にとっては終盤の問題が解けてようやく数学の得意な人達に肩を並べることができるのだ.
よって一度手をつけた問題集は最後まで絶対にやりきることは忘れないでほしい.もし途中で諦めるようなら中学生の場合は三平方の定理と立体図形,文系の高校生なら数列・ベクトルは一生かけてもできないと思った方がいい.
(冗談ではない,本気と書いてマジで言っている)
その2 もし参考書が難しい内容なのであれば易しめの参考書に変更するまたは比較的難易度の低い問題から取り組むのはOK
もし今持っている参考書が難しい内容なのであれば易しめの参考書に変更してもOKだし,参考書の難易度の低い問題だけ解いてみるのは全然ありである.
例えば青チャートの問題が難しいのであれば黄色チャート,白チャートに変更してみる.青チャートの中でも比較的難易度の低い★1や★2を積極的に進めてみる…のように学生さんなりに工夫するのはOKである.
さらに青チャートやレジェンド等の辞書のように分厚い数学参考書は問題数が多い反面計画的に勉強するのも難しいのでその中で「例題だけ解く」とか「★1, ★2の問題を徹底して取り組む」とか,全ては網羅しようとはせず広く浅くやってみる方法に関してむしろ筆者は推奨している.
しかし網羅して勉強する必要はないと言ったが,途中で諦めても良いとは筆者は言ってないので注意が必要である.
その3 良い問題集の選び方=良い解答解説本の選び方
まず良い問題集とは何だろうか?結論から先に言うとそれは丁寧な解答解説が掲載されていることである.(以前この話したような?)
今回解説した数学の勉強法を見て分かるが,解答解説をじっくり読み込み,自分が間違った原因の問題構造の層の特定とその解法についてのみ(解答解説を見ながら)暗記することはお伝えしただろう.
このフェーズにて解答解説本は必需品であり,ないと全てが始まらないといっても過言ではない.
そのため今回は良い問題集=良い解答解説本の選び方を紹介する.
1つ目:解答解説本が本編の参考本と切り離すことができるか.
要するに解答解説本が付録としてついているかである.この理由は単純で問題集と解説本が別々になっていたら見やすいからである.たまに解答解説が本の後ろについている場合がある.このような問題集は絶対買わないように.
2つ目:答えだけでなく解説がついているか.その解説が丁寧であるか.
たまにであるが答えしかついていない解答本がある.このような問題集は得意な人のための回答チェックリストであれば機能しているが,解法を会得したいこれから得意になりたい学生には全く向いていない.そのためこのような問題集は絶対買わないように.特に●●大の教授が書いている本等は要注意
3つ目:途中式の変形を省略していないか.途中式の変形理由をしっかり明記されているか.
途中式の変形を省略して理解できるのはある程度数学を理解している学生向けである.例えば理系大学生が授業で扱う問題集とかの解答解説本の途中式を省略されていることが良くある.(正直言ってやめてほしい)だがそれは数学が得意な学生だから成り立つもので,数学が苦手な学生にとってハードルが非常に高い.
比較的難易度の高い問題集や出版年代の古い問題集には要注意である.
4つ目:途中で登場する問題構造の層についての解説が丁寧に作りこまれているか.
4つ目の観点に関してはあったら神レベルの問題集である.私の中でいくつかそのような問題集は知っているが紹介しよう.1つ目は緑チャートである.

緑チャートは他色のチャート問題集とは異なり,大学共通テスト(センター試験)の問題に特化した問題集である.特に私が実際に読んでみて凄いと感じたのは短い制限時間の中で完答するためのテクニックが掲載されていることである.正解・不正解の解答解説だけでなく途中式の部分に「この式は計算せず省略してもいい」や「この計算手順はパターン化して覚える」等,早く計算するコツについても丁寧に解説されている.
2つ目は数学1対1対応の演習シリーズである.

この本は解答解説本とは別々になっていないタイプである.それだけを聞くと1つ目の話と矛盾しダメな問題集かと思われるが,この本…他の問題集とは異なり本がめちゃくちゃ大きい.そのため問題の下にぎっしりと丁寧な解答解説が掲載されており,問題文と解答解説文が文字通りに1対1に対応していて非常に見やすい.
さらにシリーズが(当時)ⅠA, ⅡB ,Ⅲの微分積分と複素数平面,双曲線等の関数に細かく分かれており,比較的にすぐ問題集をやりきることができるため達成ハードルが低めなのも素晴らしい問題集であるが故のポイントだ.
その4 期限を決めて問題集をやりきる.
その1で問題集をやりきることを解説したが,期限を設定して集中して行った方が良い.少し前にマルチタスクの話をしたが,人間は一つの事を同時に行うとかえって効率が悪いことが最近分かってきてる.
特に受験が間もない学生さんはたくさんの教科を満遍なく勉強したい気持ちは分かるが,「マルチタスクは効率が悪い」ということを頭に入れて1つの数学の問題集を**日までに達成する目標を立てて最後までやりきってほしい.
具体的に青チャート等の辞書みたいに分厚い問題集:3週間から1か月
緑チャートや数学基礎問題精構等の標準的な厚さの問題集:2週間くらい
1対1対応シリーズのような薄めの問題集:1週間くらい
が目安であろう.(当時の私は青チャート2週間達成目標でやってました)
私の個人的な意見かもしれないが目標は厳しければ厳しいほど頑張れるような気がするし,そして何よりも達成させるためにスピード感を持って勉強に取り組むことができる.受験まで少ない日数の学生は勉強にスピード感を求められるので1つの勉強法として参考にしていただきたい.
4.数学の勉強法の鉄則についてのまとめ
まとめは次のようになる.
問題集は最後までやりきる(途中で諦めてはいけない)
もし持っている問題集の難易度が高いのであれば問題集を変更したり,比較的易しい問題のみ解くのは全然OKである.
良い問題集の選び方=良い解答解説本の選び方
期限を決めて問題集をやりきる
以上である.
5. 閑話休題:PDCAについての話
皆さんはPDCAという言葉をしっているだろうか?
PDCAとは良く社会人が(ビジネスシーンで)良く使う言葉なのだが,最近学生でもこの言葉を多用するそうなので知っている人もいるだろう.
そもそもPDCAとはPlan「計画」 Do「実行」 Check「確認」 Action「対策・改善」の略称であり,多くの日本企業で横行している用語である.
よく会社の上司に「PDCAを高速でぶん回せ!!」って怒られた経験のある社会人もいるだろう.PDCA(サイクル)をできるだけ高速に回すことで目標に向かって改善+達成することができると信じて社会人は上司に怒鳴られながら嫌々内心サボりながら高速でぶん回している.
そもそも今回の数学の勉強法にPDCA関係ある?と思われるが勘の良い人であれば分かるだろう.この数学の勉強法これ自体がまさしくPDCAなのだ.

良く考えてみてほしい.
「(1):初見で解答を作成する」に関しては問題を読み取り,解答を自分なりに考えてみると捉えれば「解答の構想を練っている」とも考えられる.これについてはPDCAのPlan「計画」と同義表現なのではないだろうか?
「(1)初見で解答を作成する+(2):解答解説を読み込む」に関しては実際に手を動かして解答を作成し,正解・不正解確認後,解答解説をじっくり読み込んでいると捉えれば「解答作成+解答解説の熟読」という行動の一つとして考えられる.これについてはPDCAのDo「実行」と同義表現なのではないか?
「(2):問題構造の層の特定」に関しては解答解説を読み込んで自分が思いつかなかった・誤解していた問題構造の層と未到達の問題構造の層について把握する目的があると考えると,捉え方次第で「問題の回答を間違えた原因を確認している」とも考えられる.これについてはPDCAのCheck「確認」と同義表現なのではないだろうか?
「(3):間違えた問題構造の層に関する解法暗記」は間違えた原因を踏まえて対策および改善策を練って,それを実行していると捉えることができる.これに関してはPDCAのAction「対策・改善」と同義表現なのではないだろうか?
私はこの勉強法で「分からないなら潔く諦めて解答解説を読み込め」や「思いつかなかった・誤解している問題構造の層だけ解法暗記しなさい」,さらに「期限を決めて問題集を最後までやりきりなさい」と主張しているが.これらは必要最低限の項目数に負担を抑えることでできるだけ素早く解法暗記を行うために必要な事だから提供している.
これもPDCAサイクルを高速で回すことと同義表現なのではないだろうか?
実際にプロセスチャート図もやや複雑であるが円のようにグルグルと同じことを何度も繰り返している.
多くの日本企業がPDCA!! PDCA!!と言っているが,果たして本当にPDCAをちゃんとやっているのだろうか?制度が整っている大手企業こそPDCAシートを作成しているが,そんなシートを作成してる時点でPlan「計画」に時間をかけすぎなのではないかと思う.
正直数学の勉強法でもそうだがPlan「計画」なんて適当でいい.計画が行き詰っているのなら(解答が分からないのなら)すぐに行動して(答えを見て)原因を特定して改善策を立てればいいのに(原因の問題構造の層を特定して解法暗記でもすればいいのに)と常に思う.
何度も言うPDCAにおけるPlan「計画」は一番時間をかけなくていいと思う.大手の日本企業こそPDCAを回している気になってPDCAシートを書かせてPlan「計画」に時間を割きすぎだと思う.
以上で閑話休題とさせていただく.
ご愛読ありがとうございました.
