
アインシュタイン→シュレディンガーwithハイゼンベルク→ディラック in 1926年
シュレディンガー方程式をめぐる一連の1926年論文を読解していくと、冴えに冴えたその論理の割れ目から、シュ教授をおびやかす妖怪が次第に立ち現れていく様が見て取れます。
それは何か? 確率でございます。
詳細は後の機会に委ねます。彼の理論は、電子のふるまいそれに存在を波動と考えるものでした。事実、その方程式の解は「波動関数」と呼ばれるものです。
だがしかしところが、この方程式をより精緻なものに磨き上げていくほど、訳の分からない、もうひとつの関数が生じてきました。
シュ教授は「なんやろこれ、統計数学でよく出てくる重み関数ってやつかな」と理屈付けたものの、自分でも腑に落ちなかったのか、ややキレの悪い論述を論文中でなさっています。
「それは確率関数やー!」とシュにとっては禁断のひとことを言ってしまったのがマックス・ボルンでした。同じ1926年のことです。この論が後にノーベル物理学賞に輝くことになります。シュはというと終生、確率解釈を拒絶し続けたそうです。
ポールくん
同年にもうひとり、シュ方程式のなかに確率関数を見て取った方がいました。ポール・ディラックです。例の論文です。
五部構成なので、一つずつ見ていきましょう。冒頭ページと続くページまでが序部。論文全体の要約も兼ねています。


ChatGPTによる日本語訳を貼ろうかと思いましたが、一部の数式をこちらでうまくOCRで読み取れないままChatくんに「清書してちょ」「要約つくってちょ」「日本語に訳してちょ」と無理強いしたこともあって、ブログに貼っても読み飛ばされるであろう日本語文になってしまったので、ブログには貼らず、私の手でちゃちゃっと要点を綴っていくに留めます。

ヴェルナー・ハイゼンベルクの研究への言及からスタートです。前年(1925年)にヴェルくんが、量子力学の扉を開けることになる論文を世に問いました。これはアイディアこそピカ一でしたが未成熟なもので、ポールくんは目を通して当初投げ出していました。
ところが十日ほど経ってから再読するに、論文中盤にこんな記述がちらっとあるのに目が留まりました。「xy-yx≠0となる不思議な量が、ぼくの理論には出てくる」 ヴェルくんがそこを論文で深入りしなかったのは、頭の悪い査読者にボツ判定されるのを怖れて、それで余談っぽく挟んですませたからでした。
ポールくんは見逃さなかった。そしてこの不可換量の存在こそが新理論の本質であると考え、$${pq-qp=定数}$$ の関係式を算出。
彼の研究は、ヴェルくんとその仲間たちをびびらせました。二ヶ月前に同種の計算結果を実は出してはいたのですが、ポールくんのもののほうがずっと洗練されていて贅肉皆無の完成度だったからです。
ヴェルくんはポールくんの研究を自分たちへの追い風に感じたことと想像します。その後長く交友が続くしね。そして本論考のなかでポールくんは、ヴェル一派の最新研究を取り上げつつ、現時点での限界にも言及しています。電子がひとつの場合は計算できるけれど複数になると手に負えなくなっちゃうよね、と。
続く段落では、本論考刊行と同じ1926年前半にエルヴィン・シュレディンガーが独り勝ち的に画期的論文を輩出したことに触れています。

シュ方程式についてポールくんは「シュレディンガーは、波動関数が満たすべき微分方程式を変分原理から導出した」と述べているのに苦笑しました私。いわゆる第一論文のなかでシュはそういう風に論述してはいますが、実はその立式過程をよっく読むと、ヘンブン原理からでは導出はできないのに、できたかのような書き方をしているのです。(ここ、後日じっくり検証するので今は深追いしません)
俊英ポールくんも、1926年当時はシュの議論のトリックを見過ごしていたのだなーって少しだけ優越感。それはいいとして、シュ方程式(微分方程式です)がハミルトニアン方程式とも深く関連していることをポールくんは強調しつつ、こんな式を紹介します。

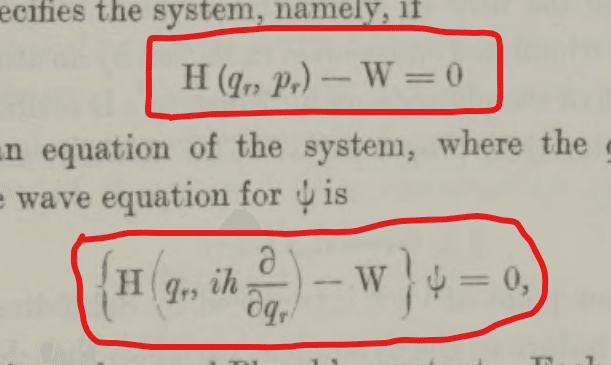
ハミルトン力学の真髄「正準変数」を一つ目の式に放り込むと、二つ目の式「シュレディンガーの波動方程式」(=シュ方程式)が導出されます。ヴェルナーくんのいわゆる行列力学が、こうしてエルヴィンくんの波動力学(波動方程式を使う)との同等性が示されるわけですねん、とポールくんは簡略に綴っています。
そして本論考の第二章、第三章、第四章、第五章がどういう内容なのかを予告していきます。②は、微分演算子を使う場合の恒等式の定義について。③は、電子が二つある場合について、対称/反対称の固有関数なら説明しきれるとする議論、④は、理想気体の分子について対称/反対称の固有関数で説明できるか試みると、光子と同じく前者の関数で説明できること、⑤は、アインシュタインが1916年の論文で、電子が電磁波(光)を吸収/放射するメカニズムの数式化を試みたことがあって、自分はそれを摂動法を使って補い完成させるというものである、と。

「以上が第一章の内容だ。第二章の解読は次回になるよワトソンくん!」

つづく⇩
