ポール・ディラックの原論文を読んでみよう（1926年：電子の遷移確率）

今回取り上げるのは、1926年8月に投稿して10月に刊行された論文 "On the Theory of Quantum Mechanics"（量子力学の理論）。ディラックがシュレディンガーの波動関数（シュはこの年の１月より立て続けに同関数についての論文を出していました）について公的に言及した最初が、おそらくこれです。

この年の少し前に、マックス・ボルンが確率解釈を提唱しています。シュレディンガー方程式の解として現れる ψ（波動関数）について「二乗すると電子の存在確率になる」と言い出したのです。シュはこのアイディアに憤慨したのですが、ボルンは自分たちが前年に提唱した行列力学の考え方とよくなじむものであると主張しました。（ちなみにこの論文でボルンは、後にノーベル物理学賞を授与）

ご承知のように、量子力学の黎明期には、ボルンらが行列を駆使して組み立てた「行列力学」（1925年）と、少し遅れてシュレディンガーが「微積（というか変分法）で解けるわい！」とかっこよく切り出した「波動力学」（1926年）の二つが対立していました。

この二つが数学的には等価であることを、シュ本人が（後世の目で見ると不完全なものでしたが）証明していました。そこにボルンが目を付けて「行列を使うと | ψ | ² を確率密度とみなしても行列要素とうまく対応するぞ」と反撃したのです。1926年のことです。

その証明はボルンではなくポール・ディラックによって、同年８月になされ、10月に刊行された論文でなされました。今回取り上げた論文のことです。

以下は論文冒頭から。

The new mechanics of the atom introduced by Heisenberg may be based on the assumption that the variables that describe a dynamical system do not obey the commutative law of multiplication, but satisfy instead certain quantum conditions. One can build up a theory without knowing anything about the dynamical variables except the algebraic lawrs that they are subject to, and can show that they may be represented by matrices whenever a set of uniformising variables for the dynamical system exists. It may be shown, however, that there is no set of uniformising variables for a system containing more than one electron, so that the theory cannot progress very far on these lines.

A new development of the theory has recently been given by Schrodinger. Starting from the idea that an atomic system cannot be represented by a trajectory, i.e., by a point moving through the co-ordinate space, but must be represented by a wave in this space, Schrodinger obtains from a variation principle a differential equation which the wave function must satisfy. This differential equation turns out to be very closely connected with the Hamiltonian equation which specifies the system, namely,

DeepL で日本語訳：
ハイゼンベルクによって導入された原子の新しい力学は、力学系を記述する変数は乗法の可換則に従わず、代わりにある量子条件を満たすという仮定に基づいている。力学的変数が従う代数法則を除いて、力学的変数について何も知らなくても理論を構築することができ、力学系を統一する変数の集合が存在すれば、いつでも行列で表現できることを示すことができる。しかし、1つ以上の電子を含む系では、統一化変数の集合は存在しない。

最近、シュレディンガーによってこの理論の新しい展開がなされた。シュレディンガーは、原子系は軌跡、すなわち座標空間内を移動する点では表現できず、この空間内の波動で表現しなければならないという考えから出発し、変分原理から波動関数が満たすべき微分方程式を得た。この微分方程式は、系を規定するハミルトニアン方程式と非常に密接に結びついていることがわかった、

この頃のディラック論文は難解な方向にどんどん向かっていく頃で、おかげで冒頭頁からして難解です。しかし要は、彼が学生時代より提唱していた q-number（q 数）で立式すれば両者うまく融合するねんという宣言です。q は quantum（量子）のイニシャル。AB - BA ≠ 0 となるような特殊な代数のための数です。積の順番を入れ替えると異なる結果になる数と述べたほうがわかりやすいでしょうか。

q 数準拠で考えていけば謎は解ける… この信念を胸にポールくんは、こんな風に話を続けていきます。

In the present paper, Schrodinger’s theory is considered in § 2 from a slightly more general point of view, in which the time t and its conjugate momentum—W are treated from the beginning on the same footing as the other variables. A more general method, requiring only elementary symbolic algebra, of obtaining matrix representations of the dynamical variables is given.

In § 3 the problem is considered of a system containing several similar particles, such as an atom with several electrons. If the positions of two of the electrons are interchanged, the new state of the atom is physically indistinguishable from the original one. In such a case one would expect only symmetrical functions of the co-ordinates of all the electrons to be capable of being represented by matrices. It is found that this allows one to obtain two solutions of the problem satisfying all the necessary conditions, and the theory is incapable of deciding which is the correct one. One of the solutions leads to Pauli’s principle that not more than one electron can be in any given orbit, and the other, when applied to the analogous problem of the ideal gas, leads to the Einstein-Bose statistical mechanics.

The effect of an arbitrarily varying perturbation on an atomic system is worked out in § 5 with the help of a new assumption. The theory is applied to the absorption and stimulated emission of radiation by an atom. A　generalisation of the description of the phenomena by Einstein’s B coefficients is obtained, in which the phases play their proper parts. This method cannot be applied to spontaneous emission.

以下はDeepLによる日本語訳：
本論文では、§2において、シュレディンガーの理論を、時間tとその共役運動量Wを他の変数と同じ立場で最初から扱うという、やや一般的な観点から考察する。初歩的な記号代数のみを必要とする、動的変数の行列表現を得るための、より一般的な方法が与えられる。

第3節では、いくつかの電子を持つ原子のような、いくつかの類似した粒子を含む系の問題を考える。二つの電子の位置が入れ替わった場合、原子の新しい状態は元の状態と物理的に区別できない。このような場合、すべての電子の座標の対称関数だけが行列で表現できると考えられる。これによって、必要な条件をすべて満たす2つの解が得られることがわかったが、理論的にはどちらが正しいかを決定することはできない。一方の解は、任意の軌道に1個以上の電子は存在できないというパウリの原理につながり、もう一方は、理想気体の類似問題に適用すると、アインシュタイン-ボースの統計力学につながる。

任意に変化する摂動が原子系に及ぼす影響は、§5において 新しい仮定の助けを借りて、§5で計算される。この理論は 原子による放射線の吸収と誘導放出に適用される。アインシュタインのB係数による現象の記述の一般化が得られる、 位相が適切な役割を果たす。この方法は 自然放出には適用できない。

「一気にけりをつけるぜ！」って感じの前振りですね。そして第５節で、シュレーディンガー方程式を摂動の視点より組み立てなおしにかかるのです。

In this section we shall consider the problem of an atomic system subjected to a perturbation from outside (e.g., an incident electromagnetic field) which can vary with the time in an arbitrary manner. Let the wave equation for the undisturbed system be

DeepL訳：
この節では、原子系が外部からの摂動（例えば、入射電磁場）を受け、その摂動が時間によって任意に変化する問題を考える。擾乱を受けていない系の波動方程式を次式とする。

そしてハミルトニアンＨをポテンシャルエネルギーＷを持ち出して、正準交換関係にシュ方程式を読みかえていく手続きに入って…

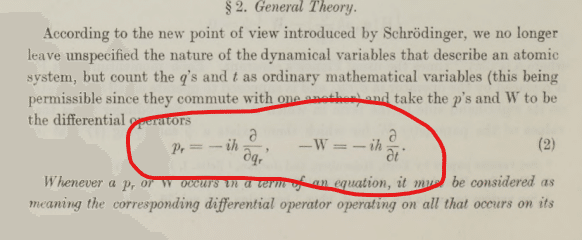
いちいち説明していくのめんどうなのでさっさと説明すると、シュ方程式に摂動論をほどこして、その結果を | ψ | ² を確率密度とみなすボルンのアイディア準拠で解釈して（もっともこの論文ではボルンのくだんのアイディアについて言及がないのでディラックは独自にたどり着いたのかも）、ボーアの振動数条件（高校物理の終盤にちらっと習うアレ）とアインシュタイン係数Ｂ（誘導放出と吸収の遷移確率に絡む係数、1916年に提唱）を導出するという、離れ業を成し遂げたのがこの論文です。

もっとも、肝心の電磁場（光の場）については立式に至らなかったので、自発放出の確率までは語れずに終わっています。そこまで行くのは翌年のあれでのことです。あれです。前回取り上げたあれのことです。

最終頁を紹介しておきます。ちなみに全17頁ですこの論文。17頁でこの濃さですのでめまいがします。以下、最終頁。

本人は明晰に語り切ったと思ったようですが、ほとんどの皆さまはそうは受け取らなかったと思われます。

［おまけ］ウィキペディアで「ボルンの規則」の解説に目を通したのですが、ボルン本人の論文とは違う、現代的解釈による説明をしているのが少しばかり気になりました。そのうえ出典とされる論文が間違って脚注に紹介されているし。英語版のミスを日本語版がそのまま踏襲しているようです。