アインシュタイン（満26歳）のノーベル賞論文は穴だらけ - Part Seven

論文の第６節を解読していきましょう。

第５節の解読はこちら。そして以下が第６節です。

日本語にすると「単色放射のエントロピーの体積依存性の式をボルツマンの原理によって解釈する」。やはりわけのわからないタイトルです。

おさらいも兼ねて説明します。「エントロピー」という、この宇宙における究極のメーターの片割れ（ちなみにもうひとつは「エネルギー」）について、アルベルトはもっと直観的体感的に語れるものにしたいと、そう願っているのがこの論文です。

 「エネルギー」あるところ「エントロピー」あり。光は電磁波ですので、いうまでもなくエネルギーを有します。すなわちエントロピーも伴います。

ここまではいいですね？

一方「エントロピー」論は、もともとはそうではなかったのですがやがて気体分子運動論の発展とともに、さらに発展していきました。

その後「エントロピー」論は、再び抽象的な数学的議論に引き戻されていったわけです。マックス・プランク教授による1900~1901年論文（＆講演録）はまさにそういう方向に進んでいくものでした。

彼は、これまで何度か繰り返したように正統派のコースを歩いてきた物理学者です。数式を丹念に積み上げていって結論に達する、そういうスタイルです。

しかしそのせいで、彼の研究の出発点となった「ウィーンの公式」が、そもそも気体分子運動のアナロジーから生まれたものなのに、その事実が数式の羅列によって消し去られてしまっているではないか ―― そうアル（26歳）くんは歯がゆさを覚えたのです。

そこでどうするか？ エントロピーの増減を、気体の体積比で考えるようにすれば、おのずと気体分子運動論という原像が戻ってくるのではないか… そう思索を深めていきました。

いいですか念押ししますよ。この頃「光は波」は揺るぎない定説となっていました。しかしプランク教授による画期的な「プランクの公式」は、光が粒子であることを暗示させるものでもありました。

彼はこの不一致について「物体が熱エネルギーを与えられると、おそらく原子のなかに何か振動するものがあって、その振動は１，２，３と整数倍になる仕組みになっている。ゆえに放たれる光はとびとびとなって、粒子状になるのだろう」と、彼らしい堅実な説を立てていました。

アルはそこまで堅実ではなかった。正統派プランクに対して、アインシュタインくんは異端児でした。

「プランク先生、あなたがそうやって背を向けたがっている気体分子運動論のアナロジーに、むしろ今一度戻ってみるべきやないですか？」と。

そして、前節（第５節）でひねり出したこの式が…

プランク教授も使った「ボルツマンの原理」のこの有名な式によく似ていることに着目して…

先ほどの（つまり第５節でひねりだした）数式を、上のボルツマン公式と同じく「Ｒ/Ｎ」が現れるよう、こんな風に変形するのです。

上二つの式が同じものであるとなると、こんな等号式が出てきますね。

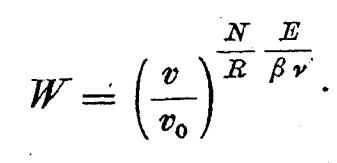
「W」については前回説明したとおりです。しかし赤で囲ったところが、私にはとても興味深く思えます。

これ「ｈ」を使えば、ここまですっきり書けてしまうのに、アルくんしないのですよ。

意地でも「ｈ」は使わん！という意地です、アルベルト（26歳）の意地。

この「ｈ」は、プランク教授の論文が初出です。光は波のはずなのだけど、彼の「プランクの公式」に従うならば、光のエネルギーはある定数の整数倍でしかありえない、そこでその定数を「ｈ」と名付けたのです。

アルはこの論文中で「ｈ」をとうとう一回も使わないでいます。使えばもっとスマートに話が進むのに使わない。これはもう当時の彼の意地ですね。「自分の研究はプランクのものとは別枠や、わしのアイディアこそが基本公理であり、彼の『ｈ』はわしのアイディアに則ったものやないので、この論文では黙殺したるねん」というところだと想像します。

代わりに彼は「エネルギー量子」（Energiequanten）という造語を使っています。赤で囲った…

赤丸のなかにある「Ｒβ ν /Ｎ」を「エネルギー量子の大きさ」と呼んでいます。光のエネルギーの最小単位のことです。プランク教授のいう「hν」です。しかし意地でも「ｈ」は使わず、どこまでも気体分子運動論のアナロジーで、プランクが発見したものと同じ概念にわしはたどり着いてみせたで！と力んでいらっしゃいます。

＊

ところでこの論文の第１節で、アルは少々理解を超えた仮定を置いていました。私の解説ではそこは触れずに済ませました。本題にさっさと入りたかったことと、今だから言いますが読んでみて彼が何を言っているのか私にはわからなかったからでした。

それで今回再読してみて、多少呑み込めてきた気がします。

この第１節で、彼は（現代の目で見ると）めちゃくちゃな仮定を置いています。

「完全に反射する壁で囲まれた空間内に、一定数の気体分子と電子が存在していて、自由に動いていて、互いに非常に接近したときに相互保存力を及ぼし合う。すなわち、気体分子運動論における気体分子のように衝突することができる」

気体分子と電子がぶつかり合う… はっきりいえば噴飯もののイメージです。中学の理科で、現代の私たちはこんなのを習います。原子の基本構造。

電子、ちっちゃいです。この絵にあるよりずっとずっとちっちゃいです。

さらにいうと、気体分子、たとえば酸素分子（O₂）と、電子の質量を比べると、前者が 32 amu で、後者が 0.0005 amu ですので、ええと、酸素分子が10トンとすると電子は156グラムですので… あははスマホですね。大型トラックに踏みつぶされるスマホ。ぺきっ。

1905年当時は、私たちが中学で習うような原子の構造は、未知のものでした。８年後ではなかったでしょうか、これに近いものが提唱されるのでは。

そういうわけでアルの「完全に反射する壁で囲まれた空間内に、一定数の気体分子と電子が存在していて、自由に動いていて、互いに非常に接近したときに相互保存力を及ぼし合う。すなわち、気体分子運動論における気体分子のように衝突することができる」という仮定は、間違ったものです。間違ったものだったのですが ――

彼がイメージしていたのは、どうやら「波」と「粒子」の両方の性質が成り立つする空間、うまくいえないのですがもっと後世に現れる、電光掲示板のようなものが超多層で重なっていく、そういうものをこの第１節で提唱していた（しようとしていた）ようです。

ここで第６節に話を戻します。

この等式を、この第６節後半でアルはひねり出しています。先ほどご紹介した式です。「プランク教授の記号は使わへん！」と意固地になって「ｈ」を使わないせいでおっかなげになってしまった、くだんの等式です。

この式に、先ほど振り返った第１節での仮定をのっけて、プランク教授も足掛かりにした「ウィーンの公式」に放り込んで全 ν（光の振動数）を積分したものを以下の式の左辺分子（青でマーク）に、そして左辺分母としてアルくんがいうところの「エネルギー量子」（Energiequanten）を最小単位として全 ν（光の振動数）を積分したもの（赤でマーク）を置くと…

右辺になにやらきりのいい値が出てきます。

気体分子運動論には、エネルギーの計算にあたってこんな係数が出てきます。

似ていますね、緑マークのところと。

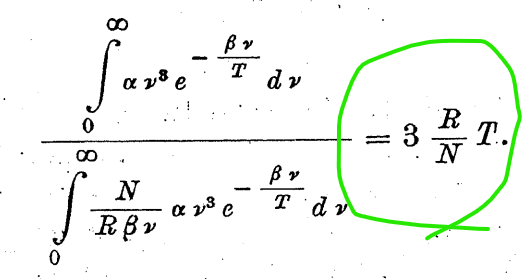
「これは果たして偶然なのだろうか？」とアルベルトは私たちに問いかけてきます。

「２１世紀における電光掲示板の、ダイオードにあたるものが、光の場には存在すると考えてみても、それほど的外れではないのではなかろうか…」とまでは論文にはないけれど、それに近いことを、26歳のアルは、当時の物理学者たちに問いかけているのです。

＊

今回のぶんで第６節まで解説しました。残るは７と８と９ですね。結論を先に言ってしまうと、アルのいう「エネルギー量子」の着想は、彼でなければ思いつけなかったであろう、ほとんどオーパーツめいた優れものではありましたが、この「エネルギー量子」アイディアからプランクの公式を導出できなければ、プランク説を塗り替えたことにはならないし、実際この論文はそこにたどり着くことなく、問題提起で終わります。途中で力尽きてしまうのです。

ただ、その後の物理学とりわけ量子論の発展ぶりをわきまえている私たちの目には、予言としか言いようのないレベルの洞察が、このあと続く第７ないし８節でさく裂していきます。

無限に広がる光の謎 —― 次回につづく！