
アインシュタイン(満26歳)のノーベル賞論文は穴だらけ - Part Five
論文の第4節を解読していきましょう。
ああ第3節の解読はこちら。そして以下が第4節です。

日本語にすると「小さい輻射密度における単色光輻射のエントロピーに関する極限則」などという、いったい何が何だかな節タイトルです。
順に解読していきましょう。この第4節の出だしで、アルくんは「ウィーンの公式」の限界について指摘します。グラフで見てもらったほうが早いかな。青紫のカーヴが「ウィーンの公式」に沿ったもので、赤いのが実際の観測データ。
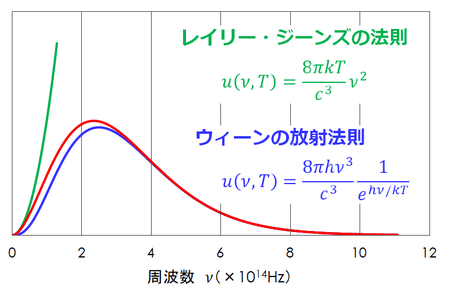
見ての通り、ウィーンのは「0」よりしばらくの区間ではうぃーんと赤カーヴから少しばかり逸れ気味です。
アルくん、この第4節の冒頭で、この「ウィーンの公式」を提示して…

これを対数関数(log が出てくるあれ)に仕立て直すことで…

という式を捻りだしてきます。「lg」とあるのは「log」のことですね。誤記ではなくてこの頃はこういう表記をしていたようです。
そこに今度は、前節で前振りしていた以下の式を提示してきます。

「黒体輻射の法則」を司る微分方程式です。素朴です。この式じたいはキルヒホフが数十年前にすでに提示していたもので、これをもとにウィーンはある仮説を立てて、くだんの「ウィーンの公式」を導出していました。
アルベルトくんはというと、ウィーンと同じくこの素朴な微分方程式を論拠にしてはいるものの、ウィーンとは違う仮定を立ててきたのが、前回説明した第3節の内容でした。
違う仮定ってなんやのー?と思った方のために、アルくんによるご説明を、以下再度引用しておきましょう。
ここでこんな仮定を置いて、以後の議論を進めたい。「放射線の観測可能な特性が、全ての周波数に対して放射線密度 (ν) が与えられた場合、完全に決定される」と。
わからへーんという声はこの際ほっといて話を進めるとですね、S(エントロピー)をめぐってこんな積分方程式が成り立つねんでとアルくんが啖呵を切ったのが、前回の第3節でした。

この数式に、細かいことは省きますが「エントロピーの極大値」が現れるという設定を加えていくと、先ほどお見せした…

これがでてくると、そういうことです。そしてここに「ウィーンの公式」を対数関数化して捻りだした、先ほどの式…

…を(アルくんは明記していないのですが、とある積分の技を使って)融合させると、こんなのがでてきます。

これの導出法はそんなに難しくないのですが、アルベルトくんどういうわけか論文中で省いてしまっているので、読むほうにすれば当時どなたも「わっきゃーせん!」だったと思います。
実は私も式を追っていて「わっきゃーせん!」でした。要は「ρ」(ローって呼びます)について0から積分して、ψ(0, v)=0 と設定すれば出てきます。第3節の議論をしっかり追えばなんとか導出できます。しかしそういう細かいことは省いて、以下本筋に戻ります。
*
「S」つまりエントロピーについて、アルくんは第3節で唐突に提唱した例の仮定をもとに、こんな式を導出します。

中辺の式はとばして、赤で括った部分が本体です。
そしてアルベルトくん、今度は同様の式を「S₀」と「v₀」について立ててきます。体積「v₀」のときエントロピーが「S₀」になるよって式。それを、上の式といっしょくたにすることで、こんなのが出てきます。

これどういうことかわかるかな? 前節で彼が提唱した仮説…
ここでこんな仮定を置いて、以後の議論を進めたい。「放射線の観測可能な特性が、全ての周波数に対して放射線密度 (ν) が与えられた場合、完全に決定される」と。
この仮説というか仮定が、上の式のなかで生きてくるのですよ。
アルくんは前年(1904年)すでに、エントロピーの考え方を気体以外のものにスマートに拡張するための試論を行っています。エントロピーは放っておくと増大することは、この頃よりずっと前に「熱力学の第二法則」として受け入れられてはいましたが、その性質上どうしてもパチンコ玉の跳ねまわる気体イメージの延長で理解されがちでした。

しかし、もし彼が前節で立てた…
ここでこんな仮定を置いて、以後の議論を進めたい。「放射線の観測可能な特性が、全ての周波数に対して放射線密度 (ν) が与えられた場合、完全に決定される」と。
という仮定とともに、先ほどの数式…

…を眺めなおすと、エントロピー(ここでSとかS₀とかあるもの)について、めっちゃ素朴に理解できてしまうのです。
以下をご覧ください。青で囲んだのが「エントロピー」の変化で、それに沿って赤で囲んだ「体積」の分数(つまり比率)が変化するのです。

このことは二つの点で非常に重要です。
①「エントロピーの増減」などという抽象的なものを「体積の増減比率」という具体的イメージで把握できる。
②「波」であるはずの光(つまり電磁波)を気体分子のイメージで把握できる。
アルベルトくん、こうやって少しずつ「光は波である」とする当時の定説に、揺さぶりをかけていくのです。

この後続く第5節で、①について数式を駆使してさらなる議論を続け、第6節で②を深化させていきます。
正直申し上げてどちらも少々回りくどい議論です。何しろ定説を揺さぶる内容ではあるけれど、真相はこうだー!ってかっこよく啖呵を切れるような、より上位の説を、この1905年3月当時のアルは形にしていなかったのです。
つまり「異議あり!その論証は証拠不十分である!!」と大見えは切れても、真犯人を特定してその推理と検証の過程を見せつけるレヴェルには達していなかったのです。

だがひるむなジム・ギャリソン検事…ではなくてアルベルト・アインシュタイン満26歳! 17年後にはノーベル賞が君を待っている!!!

第5節の解読につづく
